leetCode 229. 多数元素 II + 摩尔投票法 + 进阶 + 优化空间

229. 多数元素 II - 力扣（LeetCode）

---

给定一个大小为 n 的整数数组，找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素。

进阶：尝试设计时间复杂度为 O(n)、空间复杂度为 O(1)的算法解决此问题。 

---

（1）哈希表

class Solution {
public:
    // 哈希
    vector<int> majorityElement(vector<int>& nums) {
        unordered_map<int,int> mp;
        for(const int& a:nums) mp[a]++;
        int n = nums.size() / 3;
        int i=0;
        vector<int> ans;
        for(auto &it:mp) {
            if(it.second > n) ans.push_back(it.first); 
        }
        return ans;
    }
};

(2) 摩尔投票法

推荐看这篇文章，有关摩尔投票法的介绍：229. 多数元素 II - 力扣（LeetCode）https://leetcode.cn/problems/majority-element-ii/solutions/123170/liang-fu-dong-hua-yan-shi-mo-er-tou-piao-fa-zui-zh/① k=1时，举个栗子

• 初始化

• 执行流程 

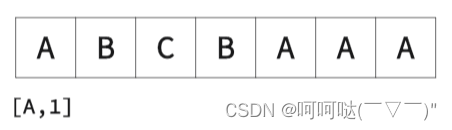
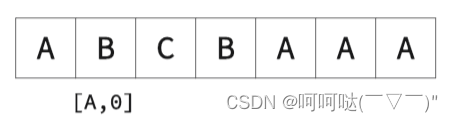
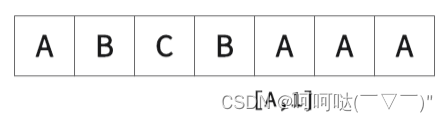
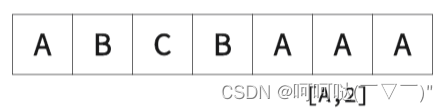
② k=2时，举个栗子 

• 初始化

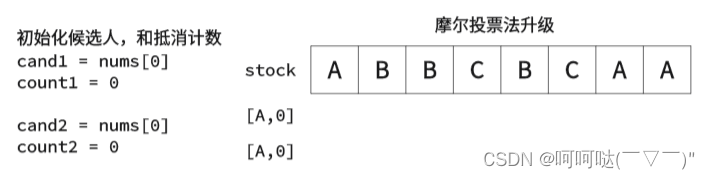
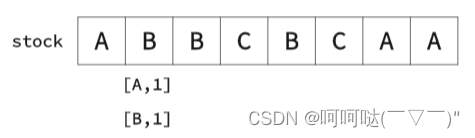
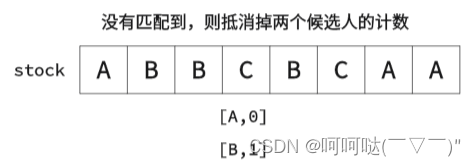
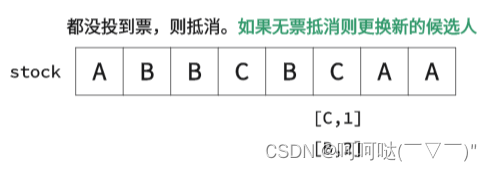
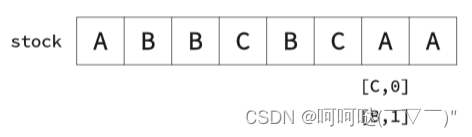
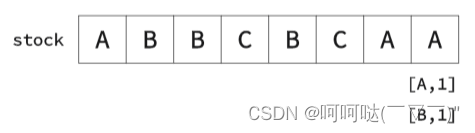
class Solution {
public:
    // 摩尔投票法
    vector<int> majorityElement(vector<int>& nums) {
        // 创建返回值
        vector<int> res;
        if (nums.empty() || nums.size() == 0) return res;
        // 初始化两个候选人candidate，和他们的计票
        int cand1 = nums[0],count1 = 0;
        int cand2 = nums[0],count2 = 0;
 
        // 摩尔投票法，分为两个阶段：配对阶段 和 计数阶段
        // (1) 配对阶段
        for(const int &num : nums) {
            // 投票
            if(cand1 == num) {count1++;continue;}
            if(cand2 == num) {count2++;continue;}
 
            // 第 1 个候选人配对
            if(count1 == 0) {
                cand1 = num;
                count1++;
                continue;
            }
 
            // 第 2 个候选人配对
            if(count2 == 0) {
                cand2 = num;
                count2++;
                continue;
            }
 
            count1--;
            count2--;
        }
 
        // (2)计数阶段 : 找到了两个候选人之后，需要确定票数是否满足大于 N/3
        count1=0;
        count2=0;
        for(const int &num : nums) {
            if (cand1 == num) count1++;
            else if (cand2 == num) count2++;
        }
 
        if (count1 > nums.size() / 3) res.push_back(cand1);
        if (count2 > nums.size() / 3) res.push_back(cand2);
        return res;
    }
};

（3）进阶版 k值投票法

class Solution {
public:
    // k值摩尔投票法
    int k = 3;
    vector<int> majorityElement(vector<int>& nums) {
        // 创建返回值
        vector<int> res;
        if (nums.empty() || nums.size() == 0) return res;
        if (nums.size() == 1) return nums;
        int n = k-1, m = 2, cands[n][m];
        memset(cands, 0, sizeof(cands));
        for(int i=0;i
            cands[i][0]=nums[0];
            // cands[i][1]=0;
        }
 
        // 摩尔投票法，分为两个阶段：配对阶段 和 计数阶段
        bool voteflag=0;
        bool matchflag = 0;
        for(const int &num : nums) {
            for(int i=0;i
                // 投票
                if(cands[i][0] == num) {cands[i][1]++;voteflag=1;break;}
                else voteflag=0;
            }
            if(voteflag) continue;
            
            for(int i=0;i
                // 第 i 个候选人配对
                if(cands[i][1] == 0) {
                    cands[i][0] = num;
                    cands[i][1]++;
                    matchflag=1;
                    break;
                }
                else matchflag=0;
            }
            if(matchflag) continue;
 
            for(int i=0;i
                cands[i][1]--;
            }
        }
        // (2) 计数阶段
        for(int i=0;i
            if(cands[i][1]==0) cands[i][0] = INT_MAX;
            cands[i][1]=0;
        }
        for(const int &num : nums) {
            for(int i=0;i
                if (cands[i][0] == num ) {
                    cands[i][1]++;
                }
        }
        for(int i=0;i
            if (cands[i][1] > nums.size() / k ) res.push_back(cands[i][0]);
        }
        return res;
    }
};

总结来自作者：我脱下短袖

• 如果至多选一个代表，那他的票数至少要超过一半（⌊ 1/2 ⌋）的票数；
• 如果至多选两个代表，那他们的票数至少要超过 ⌊ 1/3 ⌋ 的票数；
• 如果至多选m个代表，那他们的票数至少要超过 ⌊ 1/(m+1) ⌋ 的票数。
• 所以以后碰到这样的问题，而且要求达到线性的时间复杂度以及常量级的空间复杂度，直接套上摩尔投票法。

作者：我脱下短袖
链接：https://leetcode.cn/problems/majority-element-ii/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

推荐和参考文章：

229. 多数元素 II - 力扣（LeetCode）https://leetcode.cn/problems/majority-element-ii/solutions/123170/liang-fu-dong-hua-yan-shi-mo-er-tou-piao-fa-zui-zh/229. 多数元素 II - 力扣（LeetCode）https://leetcode.cn/problems/majority-element-ii/solutions/1060343/gong-shui-san-xie-noxiang-xin-ke-xue-xi-ws0rj/