递归为什么这么难？一篇文章带你了解递归

递归为什么这么难？一篇文章带你了解递归

美国计算机科学家——彼得·多伊奇(L Peter Deutsch)在《程序员修炼之道》(The Pragmatic Programmer)一书中提到“To Iterate is Human, to Recurse, Divine”——我理解的这句话为：人理解迭代，神理解递归。

毋庸置疑递归的代码是非常简洁的，但是想要理解递归也是非常不容易的，本文介绍了递归的常见场景与例题和递归的基本用法与思想，希望能帮助新人理解递归的思想，相信看完这篇文章再动手敲一下代码，一定对递归有更加深入的了解。

文章列举了一些递归的经典操作包括：斐波纳契数列、汉诺塔、冒泡排序的递归写法。以及力扣的一些链表的练习题使用递归去完成——206. 反转链表 - 力扣（LeetCode）、203. 移除链表元素、19. 删除链表的倒数第 N 个结点、83. 删除排序链表中的重复元素、82. 删除排序链表中的重复元素 II、21. 合并两个有序链表、23. 合并 K 个升序链表。

首先让我们思考：

1. 什么是递归？
2. 递归的思想是什么？
3. 怎么使用递归？
4. 使用递归应该注意什么问题？
5. 递归的时间复杂度应该怎么计算

一、什么是递归？

在计算机中，递归(Recursion)是指在函数的定义中使用函数自身的方法。实际上，递归，顾名思义，其包含了两个意思：递 和 归。

二、递归的思想是什么？

既然叫做递归，那么肯定分为“递”与“归”。

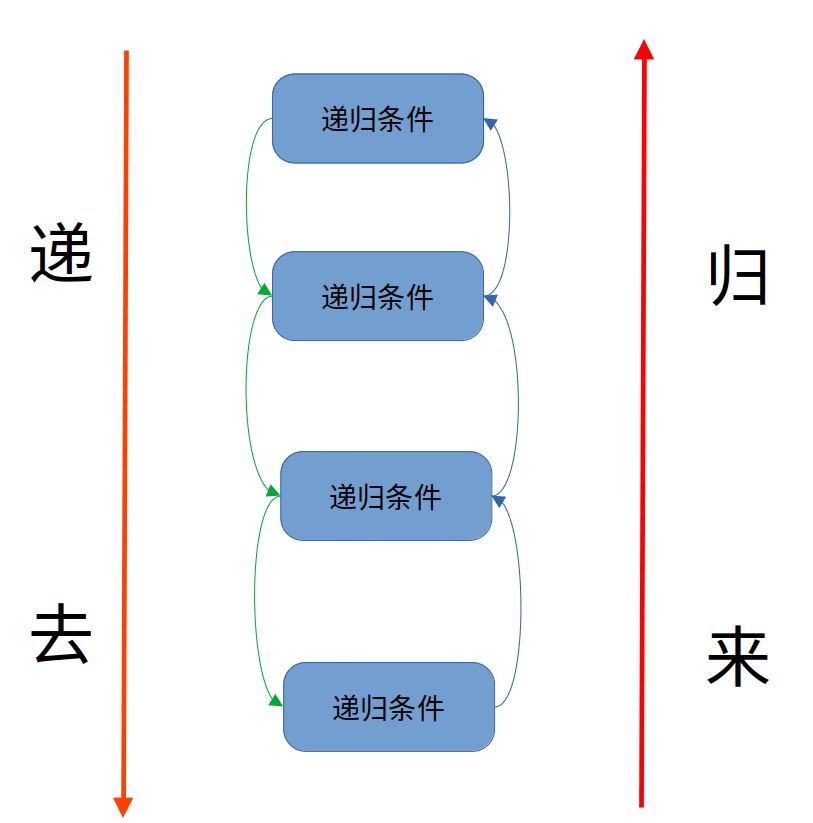
递归的基本思想就是将大规模问题转为小规模问题，问题一直被不断缩小，一直递归到符合结束条件为止。

因为每次递归都是相同的函数，所以很重要的一件事是寻找到递归的条件，找到应该如何解决大问题和小问题的同一个方法。

三、怎么使用递归

我们在了解了递归的基本概念以后就需要思考递归应该怎么用？

首先需要明确递归的三要素：

• 明确递归终止条件；

  递归既然有去有回，那么必须有一个明确的结束条件。当到达这个条件递归就会终止。

• 给出递归终止时的处理办法；

  当递归结束时，递归函数每一次返回值都需要有处理的方法，我们需要在这里给出问题的解决方法。

• 提取重复的逻辑，缩小问题规模。找出递归关系式

  寻找一个递归的关系，如何将这个问题不停分解为小问题。

注意：判断“递”还是“归”

判断是在“递”的过程中解决问题还是在“归”的过程中解决问题

四、使用递归应该注意什么？

首先我们要知道递归有两种模型。

1、在“递”的的过程中解决问题。

{
    1、递归结束条件
        
    2、问题的解决方法
        
    3、递归的等价关系，缩小规模的方法。
}
1
2
3
4
5
6
7

2、在“归”的的过程中解决问题。

{
    1、递归结束条件
        
    2、递归的等价关系，缩小规模的方法。
        
    3、问题的解决方法
}
1
2
3
4
5
6
7

这两种模型都是属于单路递归的模型，既然有单路递归那么肯定会有多路递归。

在之后的经典场景分析会介绍到冒泡排序的递归写法，就是单路递归。汉诺塔、斐波纳契数列就是属于多路递归。

五、递归的时间复杂度怎么计算？

若有递归式
$$T(n)=aT(\frac{n}{b})+f(n)$$
其中

• $T(n)$ 是问题的运行时间，$n$ 是数据规模
• $a$ 是子问题个数
• $T(\frac{n}{b})$ 是子问题运行时间，每个子问题被拆成原问题数据规模的 $\frac{n}{b}$
• $ f(n)$ 是除递归外执行的计算

令 $x={\log }_{b}a$，即 $x={\log }_{子问题缩小倍数}子问题个数$

那么
T ( n ) = { Θ ( n x ) f ( n ) = O ( n c ) 并且 c < x Θ ( n x log ⁡ n ) f ( n ) = Θ ( n x ) Θ ( n c ) f ( n ) = Ω ( n c ) 并且 c > x T(n) =

T(n)=⎩ ⎨ ⎧​Θ(nx)Θ(nxlogn)Θ(nc)​f(n)=O(nc)并且c<xf(n)=Θ(nx)f(n)=Ω(nc)并且c>x​

例1

$T(n)=16T(\frac{n}{4})+n^2$

• $a=16,b=4,x=2,c=2$
• 此时 $x=2=c$，时间复杂度 $\Theta (n^2\log n)$

例2 二分查找递归

int f(int[] a, int target, int i, int j) {
    if (i > j) {
        return -1;
    }
    int m = (i + j) / 1;
    if (target < a[m]) {
        return f(a, target, i, m - 1);
    } else if (a[m] < target) {
        return f(a, target, m + 1, j);
    } else {
        return m;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

• 子问题个数 $a=1$
• 子问题数据规模缩小倍数 $b=2$
• 除递归外执行的计算是常数级 $c=0$

$T(n)=T(\frac{n}{2})+n^0$

• 此时 $x=0=c$，时间复杂度 $\Theta (\log n)$

六、递归的实战

遇见递归请不要害怕，只是因为你做题少了而已。做完这些题一定对递归的感悟会更深刻。

1、基本运算中的递归

a、冒泡排序的递归写法

public class bubble {
    public static void main(String[] args) {
        int a[] = {1, 5, 7, 2, 0, 3, 6};
        Bubble(a, a.length - 1);
        for (int i : a) {
            System.out.println(i);
        }
    }

    public static void Bubble(int[] a, int len) {
        //1、递归结束条件
        if (len == 0) return;

        //2、处理方法
        for (int i = 0; i < len; i++) {
            if (a[i] > a[i + 1]) {
                int temp = a[i];
                a[i] = a[i + 1];
                a[i + 1] = temp;
            }
        }

        //3、递归关系，缩小问题规模
        Bubble(a, len - 1);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

通过这个简单算法，可以看出这个就属于在递的过程中解决问题的模型。

我们逐轮分析：

初始数据：{1, 5, 7, 2, 0, 3, 6}

第一轮：找到最大的数进行下沉，得到：{1, 5, 2, 0, 3, 6,7}，将7移动到最后一位，那么第二轮就不需要对7进行排序。

第二轮：找到最大的数进行下沉，因为上一轮已经找到7,那么这一轮只需要找7前面的数就行了，得到：{1, 5, 2, 0, 3, 6,7}，那么第三轮就不需要对6进行排序。

b、汉诺塔的实现

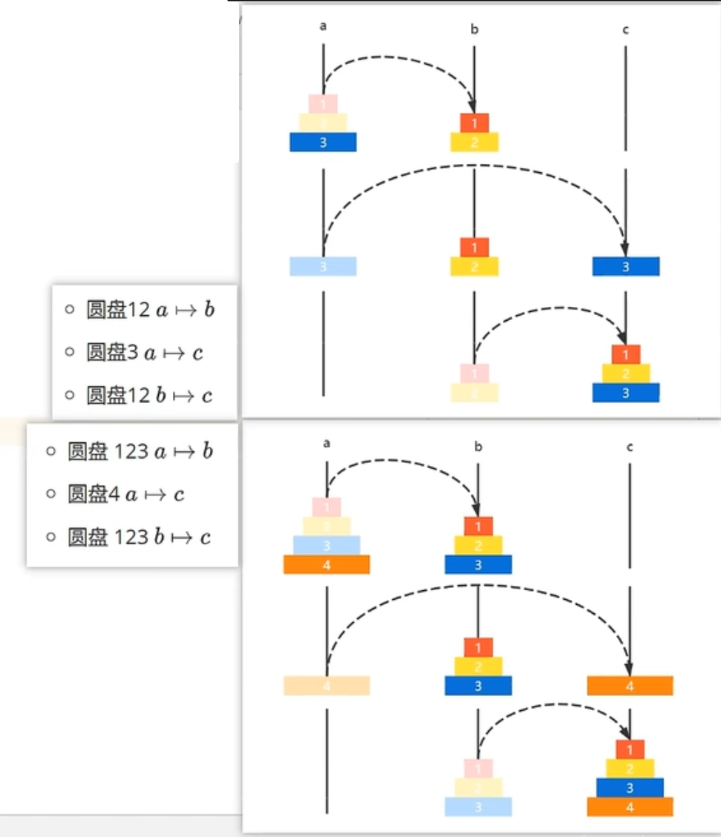
通过这个移动过程我们很容易找到一个移动规律，具体就不多说了，代码如下：

import java.util.LinkedList;

public class Hanoi {

    static LinkedList<Integer> a = new LinkedList<>();
    static LinkedList<Integer> b = new LinkedList<>();
    static LinkedList<Integer> c = new LinkedList<>();

    public static void main(String[] args) {
        long startTime = System.nanoTime();
        init(3);
        long ebdTime  = System.nanoTime();
        print();
    }

    private static void print() {
        System.out.println("**************************");
        System.out.println(a);
        System.out.println(b);
        System.out.println(c);
    }

    /**
     * 汉诺塔的递归
     * @param n 塔的层数
     * @param a 原
     * @param b 借
     * @param c 目标
     */
    public static void towerOfHanoi(int n,LinkedList<Integer> a
                    ,LinkedList<Integer> b,LinkedList<Integer> c){

        //结束条件
        if (n == 0){
            return;
        }

        //等价关系
        towerOfHanoi(n-1,a,c,b);
        //处理方法
        c.add(a.removeLast());  //将a移动到c
        //等价关系
        towerOfHanoi(n-1,b,a,c);

    }

    public static void init(int n){
        for (int i = n; i>=1; i--){
            a.add(i);
        }
        System.out.println(a);
        towerOfHanoi(n,a,b,c);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

c、斐波纳契数列

如果不知道斐波纳契的具体请看这篇文章——用C语言写爬楼梯（斐波那契数列的应用，迭代与递归）爬楼梯问题超详细，看完这一篇就够了。，就不多赘述了，这里主要介绍一下在递归中的减枝操作。

未减枝前的递归分解过程：

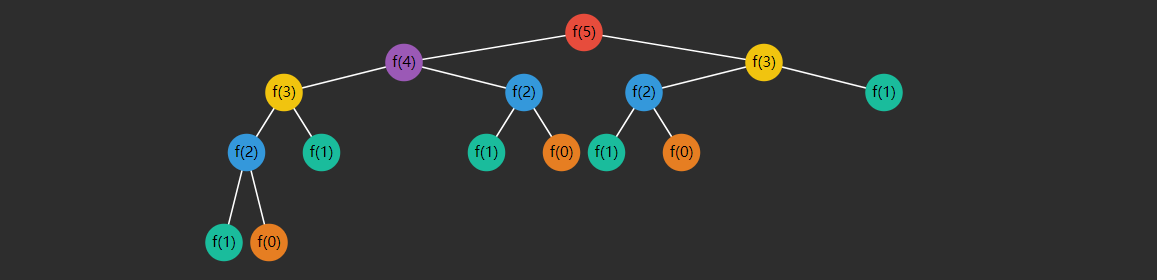
可以看到（颜色相同的是重复的）：

• $f(3)$ 重复了 2 次
• $f(2)$ 重复了 3 次
• $f(1)$ 重复了 5 次
• $f(0)$ 重复了 3 次

随着 $n$ 的增大，重复次数非常可观，如何优化呢？

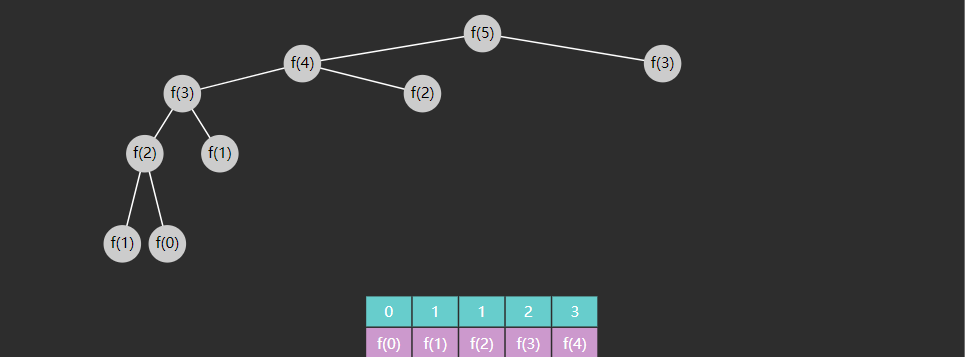
Memoization 记忆法（也称备忘录）是一种优化技术，通过存储函数调用结果（通常比较昂贵），当再次出现相同的输入（子问题）时，就能实现加速效果，改进后的代码

public class Fibonacci {
    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        for (int i = 1; i < 30; i++) {
            System.out.println(pruning(i));
        }

    }力kou

    //进行剪枝
    public static int pruning(int n){
        int[] cache = new int[n+1];
        Arrays.fill(cache,-1);
        cache[0] = 0;
        cache[1] = 1;
        return f(n,cache);
    }

    public static int f(int n,int[] cache) {

        if (cache[n] != -1){
            return cache[n];
        }

        cache[n] = f(n - 1,cache) + f(n - 2,cache);

        return cache[n];
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

在这儿我们使用了一个数组去保存了重复的运算结果。

2、链表操作的递归

在使用递归进行链表的操作时，希望大家牢记这句话：

在链表的递归过程中以单个结点操作的思想递归

a、206. 反转链表 - 力扣（LeetCode）

    /**
     * 递归实现反转链表，在同一个链表上反转
     *
     * @param head 待反转链表
     * @return 反转后的新头节点
     */
    public ListNode reverseList(ListNode head) {

        //递归结束条件
        if (head == null || head.next == null) {
            return head;
        }

        ListNode list = reverseList2(head.next);

        //操作链表进行反转
        head.next.next = head;
        head.next = null;

        System.out.println(list);
        return list;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

b、203. 移除链表元素

    /**
     * 使用递归的方法进行删除指定数据
     *
     * @param head 待处理链表
     * @param val 待删除值
     * @return 处理完成的链表
     */
    public  ListNode removeElements(ListNode head, int val) {
        if(head == null){
            return null;
        }

        if(head.val == val){
            //如果是删除该节点那么就相当于返回下一个节点的递归结果，
            // 此时上一个节点就会避开当前节点，而去链接下一个节点
            return removeElements1(head.next,val);
        }else {
            //当前节点链接到后面的链表
            head.next = removeElements1(head.next,val);
            return head;
        }

    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

c、19. 删除链表的倒数第 N 个结点

    /**
     * 使用递归的方法
     * @param head
     * @param n
     * @return
     */
    public  int recursion(ListNode head, int n){
        if(head == null){
            return 0;
        }

        int nth = recursion(head.next,n);//下一个节点的位置

        if (nth == n){
            //判断出下一个节点的的位置刚好是需要被删除的节点
            head.next = head.next.next;
        }

        return nth+1;   //当前节点的位置
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

d、83. 删除排序链表中的重复元素

    /**
     * 使用递归的方法
     *
     * @param head 待处理链表
     * @return 处理完成的链表
     */
    public static ListNode deleteDuplicates1(ListNode head) {

        if (head == null || head.next == null) {
            return head;
        }

        if (head.val == head.next.val) {
            return deleteDuplicates1(head.next);
        } else {
            head.next = deleteDuplicates1(head.next);
            return head;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

e、82. 删除排序链表中的重复元素 II

    /**
     * 使用递归的方法
     *
     * @param head 待处理链表
     * @return 处理完成的链表
     */
    public  ListNode deleteDuplicates(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }

        if (head.val == head.next.val) {

            //如果一直相同则不停移动指针，一直到找到不相同的节点为止
            ListNode t = head.next.next;
            while (t != null && t.val == head.val) {
                t = t.next;
            }

            return deleteDuplicates(t);
        } else {
            head.next = deleteDuplicates(head.next);
            return head;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

f、21. 合并两个有序链表

    /**
     * 使用递归的方法进行合并链表
     *
     * @param list1
     * @param list2
     * @return 返回添加以后的链表
     */
    public  ListNode mergeTwoLists1(ListNode list1, ListNode list2) {

        if(list1 == null){
            return list2;
        }else if (list2 == null){
            return list1;
        }

        if(list1.val < list2.val){
            list1.next = mergeTwoLists1(list1.next,list2);
            return list1;
        }else {
            list2.next = mergeTwoLists1(list1,list2.next);
            return list2;
        }

    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

g、23. 合并 K 个升序链表

    /**
     * 合并两个有序链表
     *
     * @param list1
     * @param list2
     * @return
     */
    public static ListNode mergeTwoLists(ListNode list1, ListNode list2) {

        if (list1 == null) {
            return list2;
        } else if (list2 == null) {
            return list1;
        }

        if (list1.val < list2.val) {
            list1.next = mergeTwoLists(list1.next, list2);
            return list1;
        } else {
            list2.next = mergeTwoLists(list1, list2.next);
            return list2;
        }
        

    }

    /**
     * 合并K个有序链表
     *
     * @param lists
     * @return
     */
    public  ListNode mergeKLists(ListNode[] lists) {
        if (lists.length == 0) {
            return null;
        }
        return split(lists, 0, lists.length-1);
    }

    /**
     * 进行拆分利用分治的思想(类似于快排）
     *
     * @param listNodes
     * @param i 左值
     * @param j 右值
     * @return 返回两个链表合并的结果
     */
    public static ListNode split(ListNode[] listNodes, int i, int j) {

        if(i == j){
            return listNodes[i];
        }

        int t = (i + j) / 2;    //中间值
        ListNode left = split(listNodes,i,t);
        ListNode right = split(listNodes,t+1,j);

        return mergeTwoLists(left,right);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

如果你看到这里，并且上手敲了这几道题，我相信你对于递归一定有自己的理解了。递归今天就暂时学到这吧，“To Iterate is Human, to Recurse, Divine”,你距离God又近了一步。

七、最后的最后——力扣 2698. 求一个整数的惩罚数

自己动手练练吧！2698. 求一个整数的惩罚数

这个题比较难，多动手画一下递归过程。

    public  int punishmentNumber(int n) {
        int sum = 0;
        for (int i = 1; i <= n; i++) {
            if (check(i * i, i)) {
                sum += i * i;
            }
        }
        return sum;
    }

    public  boolean check(int n, int i) {
        if (n == i) {
            return true;
        }

        int k = 10;

        /**
         *   判断数据是否可以进行拆分，可以拆分的条件为：数字应该大于10并且拆分后的尾数应该小于基准数
         *   例如：121与11,可以拆分为1和21，此时n>k符合条件，
         *   但是n%k = 21,大于11,不可能出现这样的情况符合条件
         */
        while (n >= k && n % k <= i) {
            /*
                将拆分后的数据进行比较，例如121拆分为12与1
                此时n/10 = 12,n%k = 1。得到i-(n%k) = 11
                判断出12 + 1 != i
             */
            if (check(n / k, i - (n % k))) {
                return true;
            }

            //依次从个位，百位....开始拆分。
            //例如121,第一次拆分为1,21;第二次为12,1
            k *= 10;
        }
        return false;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38