排序算法-堆积树排序法（HeapSort）

目录

排序算法-堆积树排序法（HeapSort）

1、说明

2、算法分析

3、C++代码 

---

排序算法-堆积树排序法（HeapSort）

1、说明

堆积树排序法是选择排序法的改进版，可以减少在选择排序法中的比较次数，进而减少排序时间。堆积排序法用到了二叉树的技巧，是利用堆积树来完成排序的。堆积树是一种特殊的二叉树，可分为最大堆积树和最小堆积树两种。

最大堆积树满足以下3个条件：

1. 它是一棵完全二叉树。
2. 所有节点的值都大于或等于它左右子节点的值。
3. 树根是堆积树中最大的。

最小堆积树具备以下3个条件：

1. 它是一棵完全二叉树。
2. 所有节点的值都小于或等于它左右子节点的值。
3. 树根是堆积树中最小的。

2、算法分析

1. 在所有情况下，时间复杂度均为。
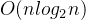2. 堆积排序法不是稳定排序法。
3. 只需要一个额外的空间，空间复杂度为。

3、C++代码 

#include
#include
using namespace std;
 
void Print(int* data, int size) {
	for (int i = 1; i < size; i++)
		cout << "[" << setw(2) << data[i] << "] ";
	cout << endl;
}
 
void Swap(int& i, int& j) {
	int temp = i;
	i = j;
	j = temp;
}
 
void ad_heap(int* data, int i, int size) {
	int j = 2 * i;
	int temp = data[i];
	int post = 0;
	while (j <= size && post == 0){
		if (j < size) {
			if (data[j] < data[j + 1])
				j++;
		}
		if (temp >= data[j])
			post = 1;
		else {
			data[j / 2] = data[j];
			j *= 2;
		}
	}
	data[j / 2] = temp;
}
 
 
void Heap(int* data, int size) {
	for (int i = (size / 2); i > 0; i--)
		ad_heap(data, i, size - 1);
 
	for (int i = size - 2; i > 0; i--) {
		Swap(data[1], data[i + 1]);
		ad_heap(data, 1, i);
	}
}
 
int main() {
	int data[9] = { 0,5,6,4,8,3,2,7,1 };
	int size = 9;
	cout << "原始数据：";
	Print(data, size);
	Heap(data, size);
	cout << "排序结果：";
	Print(data, size);
 
	return 0;
}

输出结果