【电路笔记】-波特图(Bode Diagrams)

波特图(Bode Diagrams)

1、概述

上世纪30年代末，一位名叫 Hendrick Wade Bode 的美国工程师设计了一个著名的表示法来研究频域中的交流电路。 这些图现在在电子和自动化领域仍然非常有用，被称为波特图(Bode Diagrams)。

在本文中，我们将给出表示和阅读波特图的每个必要步骤。

首先，我们提出之前需要详细说明的每个必要概念。 因此，我们将回顾一下传递函数、增益和相位的概念。

本文的后续内容包括了解如何阅读这些图表，这些图表提供了有关未知电路的大量信息。

最后一部分展示了如何绘制一些最常见的电子电路的图表。 例如，此过程对于在手动用户中以特定电路的紧凑形式共享信息很有用。

2、定义

传递函数是在讨论波特图之前需要理解的基本概念。 考虑由其传递函数 $T(j\omega )$ 定义的任何线性电子电路，并在图1 中用一个方框表示，具有一个输入端和一个输出端：

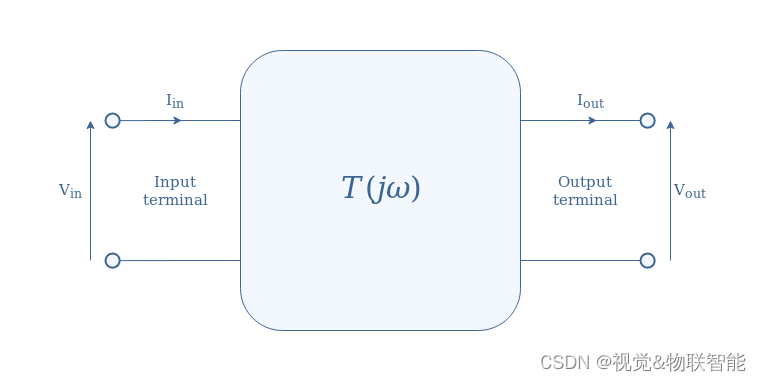
图1：线性电子电路的四极表示

传递函数由 $V_{out}=T(j\omega )\times V_{in}$ 定义，其中 $V_{in}=|V_{in}|ej\omega t$。 有时，我们可以记下 $p$ 或 $s=j\omega$，这称为拉普拉斯变量。

从这个传递函数，可以计算出两个重要的参数：

第一个是增益/幅度 ($G$)，它是通过取该复函数的范数得出的：$G=|T(j\omega )|$。 为了绘制波特图，需要考虑以分贝 ($G_{dB}$) 为单位的增益：$G_{dB}=20\log (G)$。

增益 G d B = 0 G_{dB}=0 G