-
Java 常用数据结构与算法
一、数据结构
数据结构是计算机底层存储、组织数据的方式。是指数据相互之间是以什么方式排在一起的.
通常情况下,精心选择的数据结构可以带来更高效的运行或者存储效率
1、数据结构分类
- 线性结构: 顺序表、链表、栈和队列、串、数组和广义表。
- 非线性结构: 集合、树(二叉树)、图。
2、 常用的数据结构

二、算法
算法通常都是由类的方法来实现的。前面的数据结构,比如链表为啥插入、删除快,而查找慢,平衡的二叉树插入、删除、查找都快,这都是实现这些数据结构的算法所造成的。
1、 算法的五个特征
- 有穷性:对于任意一组合法输入值,在执行又穷步骤之后一定能结束,即:算法中的每个步骤都能在有限时间内完成。
- 确定性:在每种情况下所应执行的操作,在算法中都有确切的规定,使算法的执行者或阅读者都能明确其含义及如何执行。并且在任何条件下,算法都只有一条执行路径。
- 可行性:算法中的所有操作都必须足够基本,都可以通过已经实现的基本操作运算有限次实现之。
- 有输入:作为算法加工对象的量值,通常体现在算法当中的一组变量。有些输入量需要在算法执行的过程中输入,而有的算法表面上可以没有输入,实际上已被嵌入算法之中。
- 有输出:它是一组与“输入”有确定关系的量值,是算法进行信息加工后得到的结果,这种确定关系即为算法功能。
2、算法复杂度
怎么去衡量不同算法之间的优劣呢?主要还是从算法所占用的时间和空间两个维度去考量
- 时间维度:是指执行当前算法所消耗的时间,通常用时间复杂度来描述。
- 空间维度:是指执行当前算法需要占用多少内存空间,通常用空间复杂度来描述。
因此,评价一个算法的效率主要是看它的时间复杂度和空间复杂度情况。然而有时候时间和空间却又是不可兼得的,那么我们就需要从中去取一个平衡点。
2.1 时间复杂度
表示执行时间与数据规模之间的关系
常见的时间复杂度量级有:(由低到高8个)
- 常数阶O(1)
- 对数阶O(logN)
- 线性阶O(n)
- 线性对数阶O(nlogN)
- 平方阶O(n²)
- 立方阶O(n³)
- K次方阶O(n^k)
- 指数阶(2^n)
上面从上至下依次的时间复杂度越来越大,执行的效率越来越低。
最好、最坏、平均、均摊时间复杂度
1、常数阶O(1)
- int i = 10;
- int j = 20;
- i++;
- j++;
- int num = i + j;
执行时,它并不随着某个变量的增长而增长,那么无论这类代码有多长,即使有几万几十万行,1都可以用O(1)来表示它的时间复杂度。
2、线性阶O(n)
- for (i = 1; i <= n; ++i) {
- k = i;
- k++;
- }
执行时,for循环里面的代码会执行n遍,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用O(n)来表示它的时间复杂度。
3. 对数阶O(logN)
- int i = 1;
- while (i < n) {
- i = i * 2;
- }
在while循环里面,每次都将i乘以2,乘完之后,i距离n就越来越近了。我们试着求解一下,假设循环x次之后,i就大于2了,此时这个循环就退出了,也就是说2的x次方等于n,那么x = log2n。也就是说当循环log2n次以后,这个代码就结束了。因此这个代码的时间复杂度为:O(logn)。
4. 线性对数阶O(nlogN)
- for (m = 1; m < n; m++) {
- i = 1;
- while (i < n) {
- i = i * 2;
- }
- }
将时间复杂度为O(logn)的代码循环N遍的话,那么它的时间复杂度就是n * O(logN),也就是了O(nlogN)。
5. 平方阶O(n²)
- for (x = 1; i <= n; x++) {
- for (i = 1; i <= n; i++) {
- j = i;
- j++;
- }
- }
如果把O(n)的代码再嵌套循环一遍,它的时间复杂度就是O(n²)了。
6. 立方阶O(n³)、K次方阶O(n^k)
参考上面的O(n²)去理解就好了,O(n³)相当于三层n循环,其它的类似
2.2 空间复杂度
表示存储空间与数据规模之间的关系
空间复杂度比较常用的有:O(1)、O(n)、O(n²)
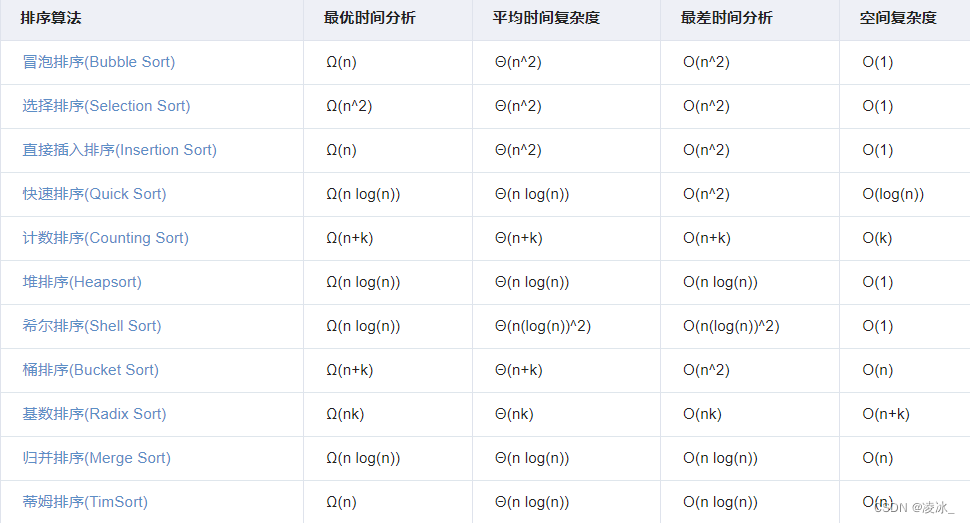
常用排序算法
-
相关阅读:
「实验笔记」华为HCIE(云服务)2.0-迁移实验-传统应用架构迁移
ChatGPT技术或加剧钓鱼邮件攻击
Excel多条件计数——COUNTIFS【获奖情况统计】
centOS7管理开放防火墙端口
节省时间的分层测试,到底怎么做?
shell_42.Linux移动参数
JRT多平台托盘优化
854. 相似度为 K 的字符串 BFS
Android基础-内存泄漏
C++学习笔记15 - struct、class、const、mutable
- 原文地址:https://blog.csdn.net/hlx20080808/article/details/134055592