对长度为n的顺序表L，编写一个时间复杂度为O（n），空间复杂度为O（1）的算法，该算法删除线性表中的所有值为x的数据元素

对长度为n的顺序表L，编写一个时间复杂度为O(n)，空间复杂度为O(1)的算法，该算法删除线性表中的所有值为x的数据元素

算法思路：
用count标记遇到x的次数，每次遇到x，count++
遇到非x的元素，把它前移count个位置

举例说明：
现有顺序表1 2 2 3 4 2 5，要求删除所有元素2
遍历到4号下标，也就是3的位置，count值为2，那么把3前移2个位置
也就是变成了1 3 2 3 4 2 5

遍历到5号下标，也就是4的位置，count值为2，那么把4前移2个位置
也就是变成了1 3 4 3 4 2 5

遍历到6号下标，是2，count++，count变为3

遍历到7号下标，也就是5的位置，count值为3，把5前移3个位置
也就是变成了1 3 4 5 4 2 5

最后length=length-count，也就是顺序表长度变成了7-3=4，那么我们顺序表也就是1 3 4 5

//初始化及打印函数

#define _CRT_SECURE_NO_WARNINGS
#include
#define MaxSize 10//定义最大长度
int InitArr[10] = { 1,2,2,3,4,2,5,2,6,7 };

typedef struct {
	int data[MaxSize];//用静态的数据存放数据元素
	int length;//顺序表当前长度
}Sqlist;//顺序表的类型定义

void print(Sqlist* L)
{
	for (int i = 0;i < L->length;i++)
	{
		printf("%d ", L->data[i]);
	}
}
//初始化一个顺序表
void InitList(Sqlist* L)
{
	for (int i = 0;i < MaxSize;i++)
	{
		L->data[i] = InitArr[i];//将所有数据元素设置为默认初始值
	}
	L->length = 10;//顺序表初始长度为0
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

对长度为n的顺序表L，编写一个时间复杂度为O(n)，空间复杂度为O(1)的算法，该算法删除线性表中的所有值为x的数据元素

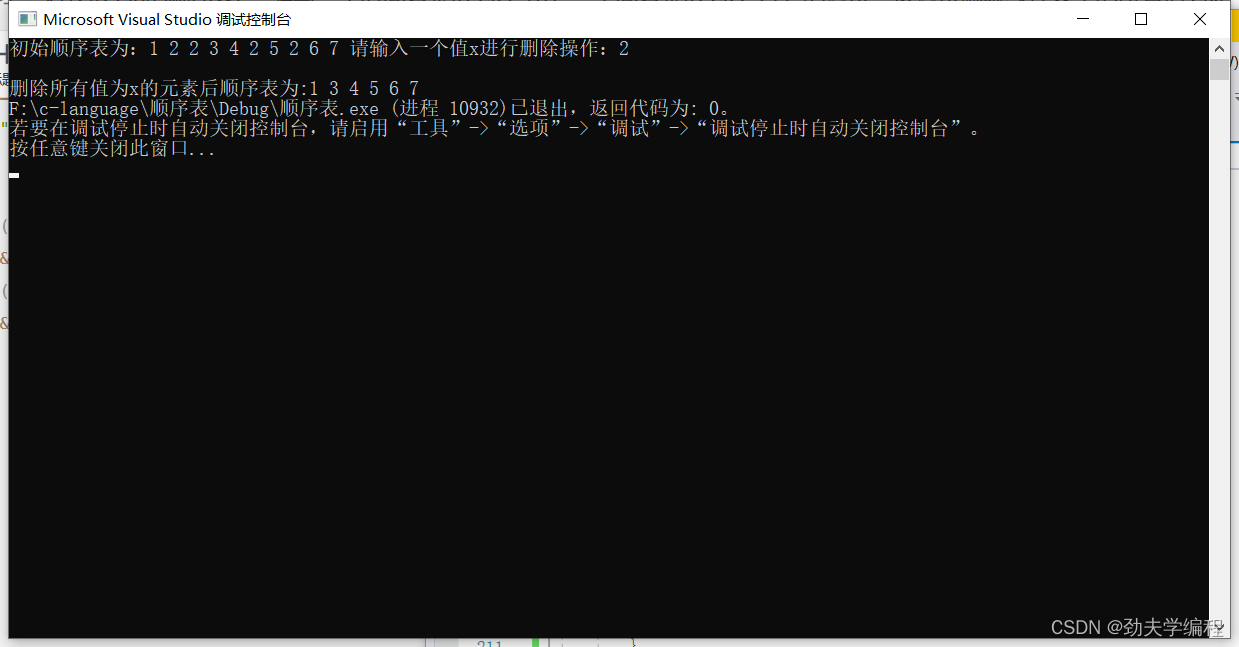
//对长度为n的顺序表L，编写一个时间复杂度为O(n)，空间复杂度为O(1)的算法，
//该算法删除线性表中的所有值为x的数据元素

//算法思路
void del_x(Sqlist* L,int x) {
	int i = 0;
	int count = 0;//标记遍历到的x的个数
	for (i = 0;i < (*L).length;i++) {
		if ((*L).data[i] == x) {
			count++;
		}
		else {
			(*L).data[i - count] = (*L).data[i];
		}
	}
	(*L).length -= count;
}
int main() 
{
	Sqlist L;
	InitList(&L);//初始化一个顺序表：1,2,2,3,4,2,5,2,6,7
	printf("初始顺序表为：");
	print(&L);

	printf("请输入一个值x进行删除操作：");
	int x = 0;
	scanf("%d", &x);


	printf("\n");
	del_x(&L,x);
	printf("删除所有值为x的元素后顺序表为:");
	print(&L);

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36