点分治介绍

一 重心

树的重心又叫树的质心：对于一颗 n 个节点的无根树，找到一个点，使得把树变成以该节点为根的有根树时，最大子树的节点数最少。换句话说，删除这个节点后最大连通块（一定是树）的节点数最少。

树的重心定义为树的某个节点，当去掉该节点后，树的各个连通分量中，节点数最多的连通分量其节点数达到最小值。

树可能存在多个重心，如图所示。

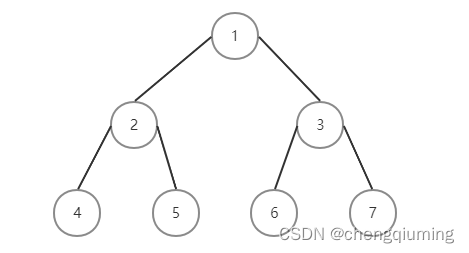
1 当去掉 1 后，树将分成两个连通块

（2,4,5）

（3,6,7）

最大连通块包含节点个数为 3。

2 当去掉 2 后，则树将分成 3 个部分。

（4）

（5）

（1,3,6,7）

最大的连通块包含 4 个节点。

第一种方法可以得到更小的最大联通分量。可以发现，其他方案不可能得到比 3 更小的值了，点 1 就是树的重心。

二 分治法

分治法指将规模较大的问题分解为规模较小的子问题，解决各个子问题后合并得到原问题的答案。树上的分治算法分为点分治和边分治。点分治经常用于带权树上的路径统计，本质上是一种带优化的暴力算法，并融入了容斥原理。对树上的路径，并不要求这棵树是有根树，无根树不影响统计结果。

分治法的核心是分解和治理。那么如何分？如何治？

数列上的分治法，通常从数列中间进行二等分，也就是说分解得到的两个子问题规模相当。若将 n 个数分解为1、n-1，则分治法会退化为暴力穷举，那么对树怎么划分呢？

对树的划分要尽量均衡，不要出现一个子问题太大，另一个子问题太小的情况。也就是说，期望划分后每棵子树的节点数都不超过 n/2。那么选择哪个节点作为划分点呢？可以选择树的重心。树的重心指删除该节点后得到的最大子树的节点数最少。

三 定理

删除重心后得到的所有子树，其节点数必然不超过 n/2。