LeetCode88——合并两个有序数组

LeetCode88——合并两个有序数组

1.题目描述：

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。
为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

2.Result01：

先将数组nums2中的元素全部存入nums1中，再对nums1数组进行排序。

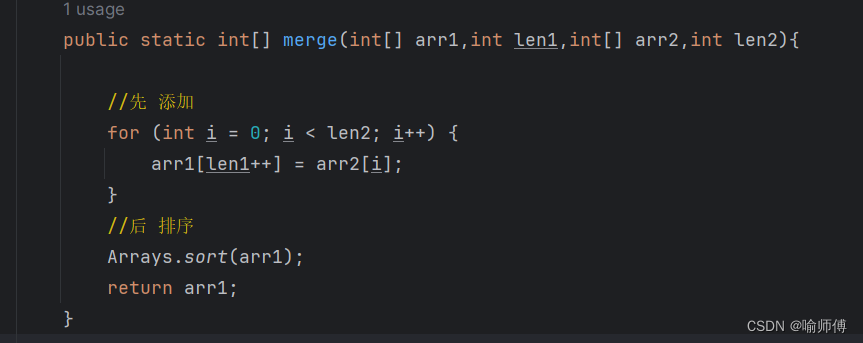
  public static int[] merge(int[] arr1,int len1,int[] arr2,int len2){

        //先 添加
        for (int i = 0; i < len2; i++) {
            arr1[len1++] = arr2[i];
        }
        //后 排序
        Arrays.sort(arr1);
        return arr1;
    }
1
2
3
4
5
6
7
8
9
10

时间复杂度：取决于排序算法的时间复杂度。
空间复杂度：O(1)

3.Result02

利用上数组非递减顺序排列的这一特性，创建一个新数组（长度与arr1相同），用两个指针分别指向两个数组元素的末端，谁比较大就放在新建数组的末端（倒序存放），最后再将新建数组的元素赋值给第一个数组。

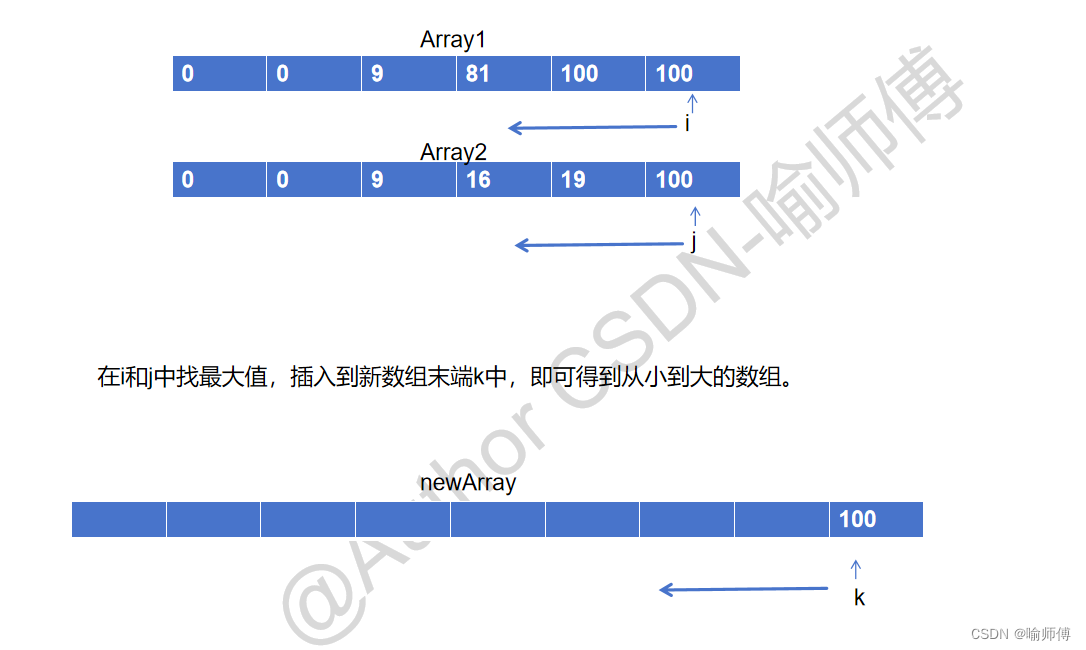
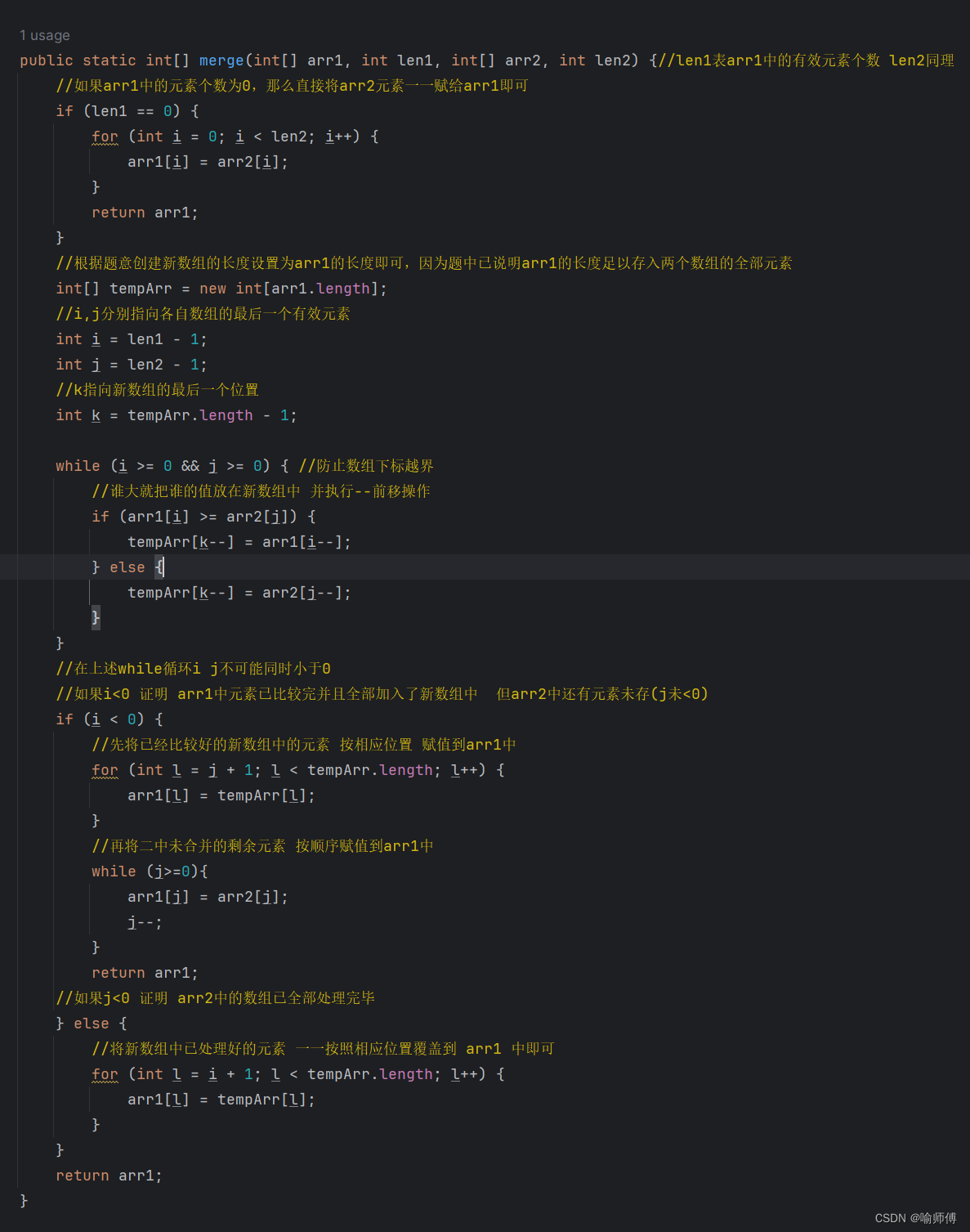
 public static int[] merge(int[] arr1, int len1, int[] arr2, int len2) {//len1表arr1中的有效元素个数 len2同理
        //如果arr1中的元素个数为0，那么直接将arr2元素一一赋给arr1即可
        if (len1 == 0) {
            for (int i = 0; i < len2; i++) {
                arr1[i] = arr2[i];
            }
            return arr1;
        }
        //根据题意创建新数组的长度设置为arr1的长度即可，因为题中已说明arr1的长度足以存入两个数组的全部元素
        int[] tempArr = new int[arr1.length];
        //i,j分别指向各自数组的最后一个有效元素
        int i = len1 - 1;
        int j = len2 - 1;
        //k指向新数组的最后一个位置
        int k = tempArr.length - 1;

        while (i >= 0 && j >= 0) { //防止数组下标越界
            //谁大就把谁的值放在新数组中 并执行--前移操作
            if (arr1[i] >= arr2[j]) {
                tempArr[k--] = arr1[i--];
            } else {
                tempArr[k--] = arr2[j--];
            }
        }
        //在上述while循环i j不可能同时小于0
        //如果i<0 证明 arr1中元素已比较完并且全部加入了新数组中  但arr2中还有元素未存(j未<0)
        if (i < 0) {
            //先将已经比较好的新数组中的元素 按相应位置 赋值到arr1中
            for (int l = j + 1; l < tempArr.length; l++) {
                arr1[l] = tempArr[l];
            }
            //再将二中未合并的剩余元素 按顺序赋值到arr1中
            while (j>=0){
                arr1[j] = arr2[j];
                j--;
            }
            return arr1;
        //如果j<0 证明 arr2中的数组已全部处理完毕
        } else {
            //将新数组中已处理好的元素 一一按照相应位置覆盖到 arr1 中即可
            for (int l = i + 1; l < tempArr.length; l++) {
                arr1[l] = tempArr[l];
            }
        }
        return arr1;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

时间复杂度：O(m+n) ，空间复杂度O(m+n)