数据结构-----图(graph)的储存和创建

目录

前言

图的储存结构

1.邻接矩阵

无向图的邻接矩阵

 有向图的邻接矩阵

网（赋权图）的邻接矩阵

 代码表示

2.邻接表

无向图的邻接表

有向图的邻接表

代码表示

3.邻接矩阵和邻接表对比

邻接矩阵

邻接表

图的创建

1.邻接矩阵创建图（网）

 2.邻接表创建图（网）

---

前言

        上一期我们学习了图的基础知识（链接：数据结构-----图(Graph)论必知必会知识-CSDN博客），这一期我们就学习怎么去储存图，和创建一个图，下面就一起来看看。

图的储存结构

1.邻接矩阵

邻接矩阵是图的矩阵表示，借助它可以方便地存储图的结构，用线性代数的方法研究图的问题。 如果一个图有 n 个顶点，其邻接矩阵 W 为 ntimes n 的矩阵，矩阵元素 w_ {ij} 表示边 (i,j) 的权重。 如果两个顶点之间没有边连接，则在邻接矩阵中对应的元素为0。

一个图G有n个顶点，就需要nxn矩阵来去表示。 

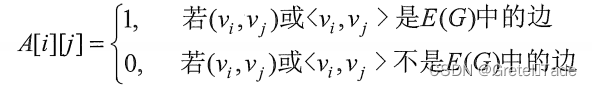
无向图的邻接矩阵

无向图的邻接矩阵特点：

• 主对角线为0，右上和左下部分对称 
• 第i个顶点的度等于第i行1的个数和，等于第i列1的个数和

 有向图的邻接矩阵

有向图的邻接矩阵特点：

• 主对角线为0，不一定对称
• 第i个顶点的出度等于第i行1的个数
• 第i个顶点的入度等于第i列1的个数
• 顶点的度=第i行元素之和+第i列元素之和

网（赋权图）的邻接矩阵

网是带有路径长度的图，所以对比上面的矩阵，我们只需要把通路1，换成路径的长度即可。

 代码表示

#define Maxnum 100//最大顶点数
//数据类型
typedef struct d { 
	char id[10];
	//……
}
ElemType;
//图的邻接数组
typedef struct graph {
	ElemType vexs[Maxnum];//图数据
	int arcs[Maxnum][Maxnum];//二维数组
	int vexnum;//点数
	int arcnum;//边数
}Graph;

2.邻接表

邻接表是图的一种最主要存储结构,用来描述图上的每一个点。对于图的每个顶点建立一个容器（ n个顶点建立 n 个容器），第 i 个容器中的结点包含顶点vi 的所有邻接顶点。

一个邻接表需要两种存储结构：顶点表结点和边表结点 

• 顶点:
  •  按编号顺序将顶点数据存储在一维数组中
• 关联同一顶点的边 (以顶点为尾的弧)
  • 用线性链表存储

无向图的邻接表

特点:

• 邻接表不唯一
• 若无向图中有 n个顶点e条边，则其邻接表需 n个头结点和2e 个表结点。适宜存储稀疏图。

有向图的邻接表

特点:

• 找出度易找入度难
• 顶点 vi的出度为第i个单链表中的结点个数。
• >顶点 vi的入度为整个单链表中邻接点域值是 i-1的结点个数。

代码表示

//数据结构体
typedef struct d {
	char id[10];//字符串编号
	//………………
}ElemType;
//边节点存储结构
typedef struct arcnode {
	int index;//指向顶点的位置
	int weight;//权
	struct arcnode* nextarc;//指向下一个边节点
}Anode;
//顶点结点存储结构
typedef struct vexnode {
	ElemType data;
	Anode* firstarc;
}Vhead;
//图结构
typedef struct {
	Vhead* vertices;
	int vexnum;
	int arcnum;
}Graph;

3.邻接矩阵和邻接表对比

邻接矩阵

 优点

• 直观、简单、好理解
• 方面检查任意一对顶点间是否存在边
• 方便找任一顶点的所有“邻接点”（有边直接相连的顶点）
• 方便计算任一顶点的“度”

缺点

• 不便于增加和删除顶点
• 浪费空间——存稀疏图 (点很多而边很少)有大量无效元素，但是对密图 (特别是完全图) 还是很合算的
• 浪费时间——统计稀疏图中一共有多少条边

邻接表

优点

• 对于稀疏图来说，邻接表比邻接矩阵更加省空间。
• 方便遍历某个顶点的所有邻接点，时间复杂度为 O (degree)。
• 邻接表算法实现简单，易于修改和扩展。

 缺点

• 重边不好处理 判重比较麻烦 ，还要遍历已有的边，不能直接判断
• 对确定边的操作效率不高
• 不方便计算顶点的入度

图的创建

1.邻接矩阵创建图（网）

下面代码是无向网的创建 

#include
#include
 
#define Maxint 32767
#define Maxnum 100//最大顶点数
//数据类型
typedef struct d { 
	char id[10];
	//……
}
ElemType;
//图的邻接数组
typedef struct graph {
	ElemType vexs[Maxnum];//图数据
	int arcs[Maxnum][Maxnum];//二维数组
	int vexnum;//点数
	int arcnum;//边数
}Graph;
 
//节点id查找下标
int Locate_vex(Graph G, char* id) {
	for (int i = 0; i < G.vexnum; i++)
		if (strcmp(G.vexs[i].id,id)==0)
			return i;
	return -1;
}
 
//构造邻接矩阵(无向图，对称矩阵)(有向图)赋权图
void Create_graph(Graph* G) {
	printf("请输入顶点个数和边的个数：\n");
	scanf("%d %d", &G->vexnum, &G->arcnum);//输入点数边数
	printf("请输入顶点数据:\n");
	for (int i = 0; i < G->vexnum; i++) {
		scanf("%s", G->vexs[i].id);
	}
	for (int x = 0; x < G->vexnum; x++) {
		for (int y = 0; y < G->vexnum; y++) {
			if (x == y)
				G->arcs[x][y] = 0;//对角线初始化为0
			else
				G->arcs[x][y] = Maxint;//其他初始化为Maxint
		}
	}
	printf("请输入边相关数据:\n");
	for (int k = 0; k < G->arcnum; k++) {
		char a[10], b[10];
		int w;
		scanf("%s %s %d", a, b, &w);
		//a->b
		int i = Locate_vex(*G, a);
		int j = Locate_vex(*G, b);
		//矩阵赋值
		G->arcs[i][j] = w;
		G->arcs[j][i] = w;//删掉这个，表示有向图
	}
}
 
//输出矩阵
void print_matrix(Graph G) {
	printf("矩阵为：\n");
	for (int i = 0; i < G.arcnum; i++) {
		for (int j = 0; j < G.arcnum; j++)
			printf("%-5d ", G.arcs[i][j]);
		printf("\n");
	}
	printf("图的顶点个数和边数：%d,%d\n", G.vexnum, G.arcnum);
}

结果如下： 

输入图的结构如下所示： 

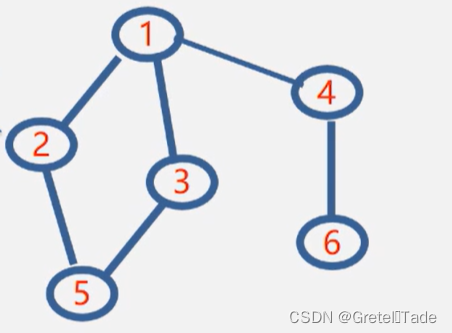
 2.邻接表创建图（网）

对于邻接表的创建，我们是先去创建好顶点表数组，然后通过遍历和头插法把数据作为边表节点插入到顶点表的后面，最后形成邻接表链。代码如下：

#include
#include
//数据结构体
typedef struct datatype {
	char id[10];//字符串编号
	//………………
}ElemType;
//边节点存储结构
typedef struct arcnode {
	int index;//指向顶点的位置
	int weight;//权
	struct arcnode* nextarc;//指向下一个边节点
}Anode;
//顶点结点存储结构
typedef struct vexnode {
	ElemType data;
	Anode* firstarc;
}Vhead;
//图结构
typedef struct {
	Vhead* vertices;
	int vexnum;
	int arcnum;
}Graph;
 
//顶点查找下标
int Locate_vex(Graph G, ElemType v) {
	for (int i = 0; i < G.vexnum; i++)
		if (strcmp(G.vertices[i].data.id,v.id)==0)
			return i;
	return -1;
}
 
//创建头节点
void Create_vexhead(Graph *G,int n) {
	G->vertices = (Vhead*)malloc(sizeof(Vhead) *n);
	if (!G->vertices) {
		printf("ERROR\n");
		exit(-1);
	}
	else {
		for (int i = 0; i < n ; i++) {
			scanf("%s", G->vertices[i].data.id);
			G->vertices[i].firstarc = NULL;
		}
	}
}
//创建一个边节点
Anode* Create_arcnode(int loca, int w) {
	Anode* arc = (Anode*)malloc(sizeof(Anode));
	if (!arc)
	{
		printf("ERROR\n");
		exit(-1);
	}
	arc->index = loca;
	arc->nextarc = NULL;
	arc->weight = w;
	return arc;
}
//创建邻接表(无向图)（有向图）
void Create_graph(Graph* G) {
	printf("输入顶点数和边数:\n");
	scanf("%d %d", &G->vexnum, &G->arcnum);
 
	printf("输入顶点数据:\n");
	Create_vexhead(G, G->vexnum);
 
	printf("输入边数据：\n");
	for (int k = 0; k arcnum; k++) {
		ElemType a, b;
		int w;
		scanf("%s%s%d", a.id, b.id, &w);
		int i = Locate_vex(*G, a);
		int j = Locate_vex(*G, b);
		//头插法
		//a->b
		Anode* p = Create_arcnode(j, w);
		p->nextarc = G->vertices[i].firstarc;
		G->vertices[i].firstarc = p;
		//如果创建有向图的话，直接把下面的代码删掉即可
		//b->a
		Anode* q = Create_arcnode(i, w);
		q->nextarc = G->vertices[j].firstarc;
		G->vertices[j].firstarc = q;
	}
}
 
//访问
void visit(Graph G, int index) {
	printf("%s ", G.vertices[index].data.id);
}
 
//输出图
void print(Graph G) {
    printf("以下是图的顶点连接关系：\n");
	for (int i = 0; i < G.vexnum; i++) {
		printf("%s:", G.vertices[i].data.id);
		Anode* cur= G.vertices[i].firstarc;
		while (cur) {
			visit(G, cur->index);
			cur = cur->nextarc;
		}
		printf("\n");
	}
	printf("顶点和边数分别是：%d %d\n", G.vexnum, G.arcnum);
}

测试结果：

好了，以上就是今天的全部内容了，我们下一期学习图的遍历，下次见咯！ 

分享一张壁纸：