Towards a Rigorous Evaluation of Time-series Anomaly Detection（论文翻译）

1 Introduction

  随着工业4.0加速系统自动化，系统故障的后果可能会产生重大的社会影响（Baheti和Gill 2011; Lee 2008; Lee，Bagheri和Kao 2015）。为了防止这种故障，检测系统的异常状态比以往任何时候都更加重要，并且正在以异常检测（AD）的名义进行研究。与此同时，深度学习在对从大型系统的众多传感器和执行器收集的多变量时间序列数据进行建模方面表现出了有效性（Chalapathy and Chawla 2019）。因此，各种时间序列AD（TAD）方法已经广泛采用深度学习，并且它们中的每一种都通过报告比之前的方法更高的F1分数来证明其自身的优越性（Choi et al. 2021年）。对于一些数据集，报告的F1得分超过0.9，这给今天的TAD能力留下了令人鼓舞的印象。
  然而，大多数目前的TAD方法测量F1评分后，应用一个特殊的评价协议命名为点调整（PA），由Xu等人提出。（Audibert et al. 2020;沈，李，和郭2020; Su等人，2019）。PA的工作原理如下：如果连续异常段中的至少一个时刻被检测为异常，则认为整个段被正确地预测为异常。典型地，F1分数是用调整的预测（在下文中由F1_PA表示）来计算的。如果在没有PA的情况下计算F1分数，则将其表示为F1。 PA协议的提出是基于在异常期间内的单个警报足以采取系统恢复的措施。它已经成为TAD评估中的基本步骤，并且以下一些研究仅报道了F1_PA而没有F1（Chen et al. 2021年）。较高的F1_PA已指示较好的检测能力。
  然而，PA有一个高估模型性能的可能性很大。典型的TAD模型产生通知输入异常程度的异常分数，并且如果该分数高于阈值则预测异常。使用PA，来自随机生成的异常评分的预测和良好训练的模型的预测变得相同，如图1-（a）所示。

图1：（a）PA使不同的异常评分难以区分。黑线、灰色区域和虚线分别指示异常分数、GT异常段和TAD阈值。在应用PA之后，针对信息性和随机异常分数的预测退化为相同的调整后的预测（红色）。

  黑色实线表示两种不同的异常分数; 上面的线示出了来自良好训练的模型的信息分数，而下面的线是随机生成的。阴影区域和虚线分别指示地面实况（GT）异常段和TAD阈值。信息分数（上图）是理想的，因为它们仅在GT段期间较高。相比之下，随机生成的异常评分（下图）在GT段内仅超过阈值一次。尽管存在差异，但PA之后的预测变得不可区分，如红线所示。 如果随机异常分数可以产生与熟练检测模型一样高的F1_PA，则难以得出具有较高F1_PA的模型比其他模型表现更好的结论。
  我们在第5节中的实验结果表明，随机异常分数可以推翻大多数最先进的方法（图1-（B））。

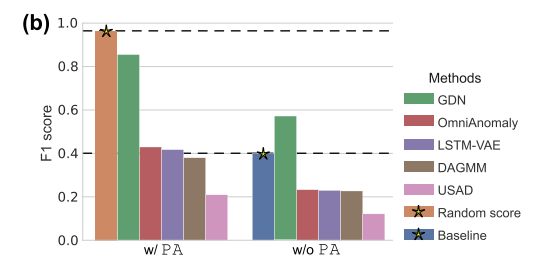
图1：(b)现有的方法未能超过随机生成的异常分数的F1_PA（左），并且即使当PA被禁止用于WADI数据集时，也没有显示出对新提出的基线（右）的改进。
  出现的另一个问题是PA是否是TAD方法评估中的唯一问题。到目前为止，只报道了绝对F1，没有试图建立基线和相对比较。如果二元分类器的准确率为50%，则尽管是明显较大的数字，但它与随机猜测没有太大区别。同样，应讨论TAD的适当基线，并应根据与基线相比的改进来评估未来的方法。根据我们的观察，现有的TAD方法似乎没有得到显着的改善，本文提出的基线。此外，一些方法未能超过它。我们对一个基准数据集的观察总结在图1-（b）的右侧。
  在本文中，我们提出了一个问题，是否目前的TAD方法，声称带来显着的改进进行了适当的评估，并提出了第一次严格的评估TAD的方向。我们的贡献总结如下：

• 我们发现，PA，一个奇特的评估协议，大大高估了现有方法的检测性能。
• 我们表明，在没有PA的情况下，现有方法在基线上没有（或大多数是微不足道的）改进。
• 基于我们的发现，我们提出了一个新的基线和评估协议，用于严格评估TAD。

2 背景

2.1 Types of anomaly in time-series signals（时间序列信号中的异常类型）

  各种类型的异常存在于数据集中（Choi et al. 2021年）。上下文异常表示具有与正常信号不同形状的信号。集体异常指示在一段时间内累积的少量噪声。点异常指示由于信号值的快速增加或减少而与预期范围的暂时和显著偏差。点异常是目前TAD数据集中最主要的类型。

2.2 Unsupervised TAD（无监督的网络）

  典型的AD设置假定在训练时间期间仅可访问正常数据。因此，无监督方法是TAD最合适的方法之一，TAD训练模型以仅在正常信号中学习共享模式。最终目标是根据输入的异常程度将不同的异常分数分配给输入，即，分别用于正常和异常输入的低异常分数和高异常分数。基于重构的AD方法训练模型，以最小化正常输入与其重构之间的距离。在测试时间的异常输入导致大距离，因为它是难以重建的。距离或重建误差用作异常分数。基于预测的方法训练模型以预测将在正常输入之后到来的信号，并采取地面实况和预测信号之间的距离作为异常分数。每个类别的详细示例请参阅附录。

2.3 Assessment of TAD evaluation（评估可持续发展评价）

  已经有几种方法指出了当前TAD评估中的缺陷。(Wu和Keogh 2021）提出了基准TAD数据集的局限性，并表明简单的检测器，所谓的单线性，对于一些数据集是足够的。他们还提供了几个合成数据集。(Lai等人，2021）为异常类型（例如，点与模式），并引入了根据新标准合成的新数据集。相比之下，我们提出了TAD评估中的陷阱：PA高估的风险和基线的缺失以及解决方案。如果陷阱没有解决，它是不可能的，以评估是否改进的TAD方法是显着的，即使与上述论文提出的更好的数据集。

3 Pitfalls of the TAD evaluation（评估的陷阱）

3.1 Problem formulation（问题公式化）

  首先，我们将在时间T期间从N个传感器观察到的时间序列信号表示为X = {x1，…xT}，x_t ∈ R^N。作为常规方法，其被归一化并分成一系列窗口W = {w1，…wT-τ+1}，其中wt = {xt，…，xt+τ−1}，τ是窗口大小。仅针对测试数据集给出地面真值二元标签yt ∈ {0，1}，指示信号是否为异常（1）或不是（0）。TAD的目标是预测测试数据集中所有窗口的异常标签。通过将异常分数A（w_t）与如下给出的阈值δ进行比较来获得标签：

  A（wt）的示例是原始输入与其重构版本之间的均方误差（MSE），其定义如下：

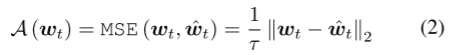
  其中，w = fθ（wt）表示来自用θ参数化的重建模型fθ的输出。这个公式表示A(wt)是预测值w_t与真实值$\widehat{wt}$之间的均方误差（Mean Squared Error，MSE）除以一个常数$\tau$。计算方法是将它们的差值平方，然后求平均。在这里，除以$\tau$是为了标准化。
标记后，精确度（P）、召回率（R）和F1得分计算如下：
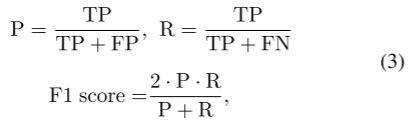  其中TP、FP和FN分别表示真阳性、假阳性和假阴性的数量。
  精确度（Precision）： 精确度是指在所有被分类为正例的样本中，确实是正例的比例。TP 是真正例数（True Positives），FP 是假正例数（False Positives）。
  召回率（Recall）： 召回率是指在所有实际正例中，被正确分类为正例的比例。FN 是假负例数（False Negatives）。
  F1分数（F1 score）： F1分数是精确度和召回率的调和平均值，它综合考虑了模型的假正例和假负例的影响。F1分数的取值范围在0到1之间，越接近1表示模型的性能越好。

  所述异常测试数据集可以包含持续几个时间步长的多个异常段。我们将S表示为M个异常段的集合;即，S = {S1，…，SM}，其中Sm = {Sm，.，tm_s和tm_e分别表示Sm的开始和结束时间。如果Sm中至少有一次异常评分高于δ，则PA将所有t ∈ Sm的Δ yt调整为1。使用PA，Eq.1变更如下：

  F1_PA表示使用调整后的标签计算的F1分数。

3.2 Random anomaly score with high F1_PA（F1_PA高的随机异常评分）

  在本节中，我们证明了PA协议高估了检测能力。我们从抽象分析的P和R的方程3，并且我们在数学上表明，随机生成的A（wt）可以实现接近1的高F1PA值。根据等式3，因为F1评分是P和R的调和平均值，所以它还取决于TP、FN和FP。如等式4所示：PA增加TP，降低FN，而维持FP。因此，在PA之后，P、R以及因此F1分数只能增加。PA的增加会增加TP（真正例），降低FN（假负例），而FP（假正例）保持不变。这意味着在PA（性能指标或阈值）增加之后，F1分数会增加，因为精确度和召回率都有可能提高。
   在一个二分类问题中，我们通常将预测值A(wt)与阈值比较，如果A(wt)大于阈值，则将样本分类为正例（1），否则分类为负例（0）。当阈值（PA）增加时，即对A(wt)的要求更高，只有当A(wt)非常接近真实值时才会被分类为正例。这会导致以下影响：

• 增加TP（真正例）：因为阈值更高，只有当A(wt)非常接近真实值时才能被正确分类为正例，这样可以减少将负例错误分类为正例的可能性，从而增加真正例的数量。
• 降低FN（假负例）：同样的原因，由于阈值更高，只有真实值与预测值非常接近才会被分类为正例，因此减少了将正例错误分类为负例的可能性，从而降低了假负例的数量。
• FP（假正例）保持不变：由于阈值的增加，只有在A(wt)与真实值非常接近的情况下才会被分类为正例，所以将负例错误分类为正例的可能性减小。因此，假正例的数量相对保持不变。

  接下来，我们证明F1_PA可以很容易地接近1。首先，R被重述为条件概率，如下所示：

  让我们假设A（wt）是从均匀分布U（0，1）中提取的。我们使用0 ≤ δ’ ≤ 1来表示该假设的一个阈值。如果只存在一个异常段，即，S = { {ts，…，te}}，PA之后的R可以表示如下，参考Eq.4：


其中，$\gamma$ = Pr（t ∈ S）是测试数据集异常率，Pr（A（w_t’）< δ \delta