-
多通道图片的卷积过程
多通道(channels)图片的卷积
如果输入图片是三维的(三个channel),例如(8,8,3),那么每一个filter的维度就是(3,3,3),每一个filter的channel要与图片的channel数目一样。
所以求卷积的过程是将每个通道分别求卷积,然后将三个通道相加得到最后的特征图。最后特征图的维度的最后一个channel与利用了多少个filter有关。
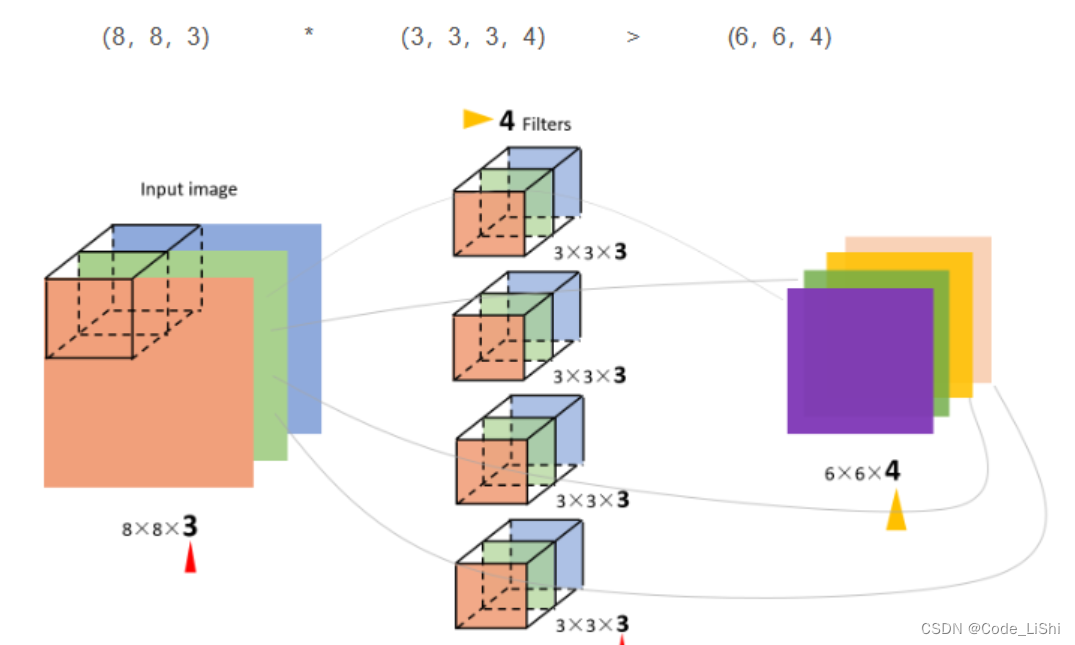
同时有4个filter图中的输入图像是(8,8,3),filter有4个,大小均为(3,3,3),得到的输出为(6,6,4)。
我觉得这个图已经画的很清晰了,而且给出了3和4这个两个关键数字是怎么来的,所以我就不啰嗦了(这个图画了我起码40分钟)。其实,如果套用我们前面学过的神经网络的符号来看待CNN的话,
- 我们的输入图片就是X,shape=(8,8,3);
- 4个filters其实就是第一层神金网络的参数W1,,shape=(3,3,3,4),这个4是指有4个filters;
- 我们的输出,就是Z1,shape=(6,6,4);
- 后面其实还应该有一个激活函数,比如relu,经过激活后,Z1变为A1,shape=(6,6,4);
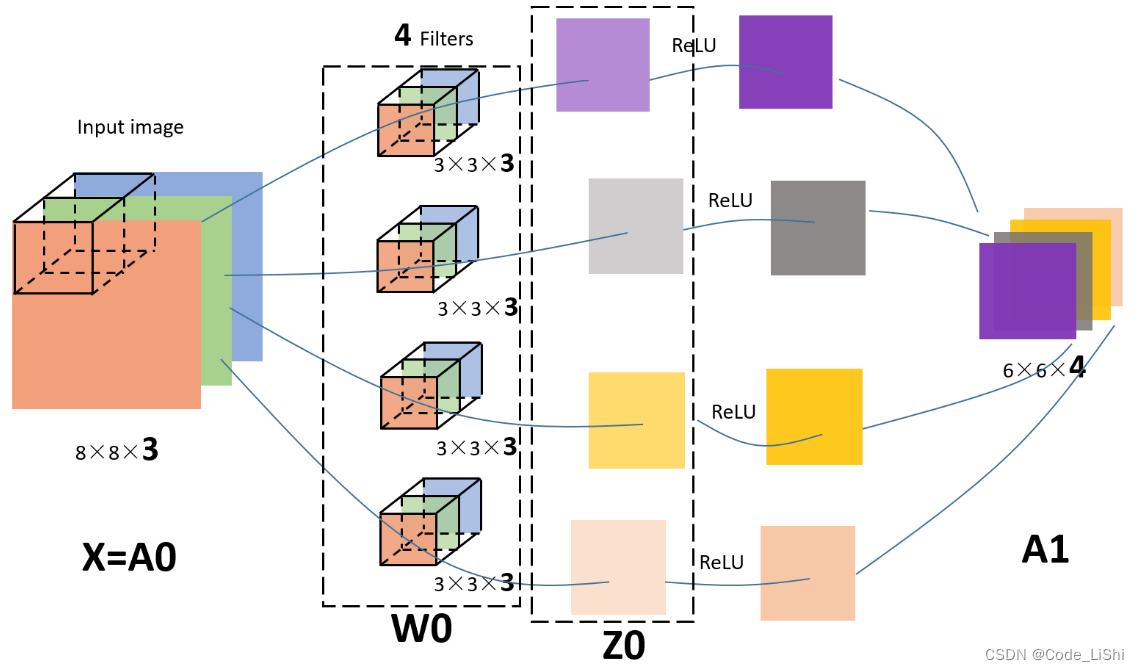
所以,在前面的图中,我加一个激活函数,给对应的部分标上符号,就是这样的:
二 CNN的构成
上面我们已经知道了卷积(convolution)、池化(pooling)以及填白(padding)是怎么进行的,接下来我们就来看看CNN的整体结构,它包含了3种层(layer):
1 Convolutional layer (卷积层–CONV)
由滤波器filters和激活函数构成。
一般要设置的超参数包括filters的数量、大小、步长,以及padding是“valid”还是“same”。当然,还包括选择什么激活函数。2 Pooling layer (池化层)
这里里面没有参数需要我们学习,因为这里里面的参数都是我们设置好了,要么是Maxpooling,要么是Averagepooling。
需要指定的超参数,包括是Max还是average,窗口大小以及步长。
通常,我们使用的比较多的是Maxpooling,而且一般取大小为(2,2)步长为2的filter,这样,经过pooling之后,输入的长宽都会缩小2倍,channels不变。3 Fully Connected layer (全连接层–FC)
这个前面没有讲,是因为这个就是我们最熟悉的家伙,就是我们之前学的神经网络中的那种最普通的层,就是一排神经元。因为这一层是每一个单元都和前一层的每一个单元相连接,所以称之为“全连接”。
这里要指定的超参数,无非就是神经元的数量,以及激活函数。接下来,我们随便看一个CNN的模样,来获取对CNN的一些感性认识:
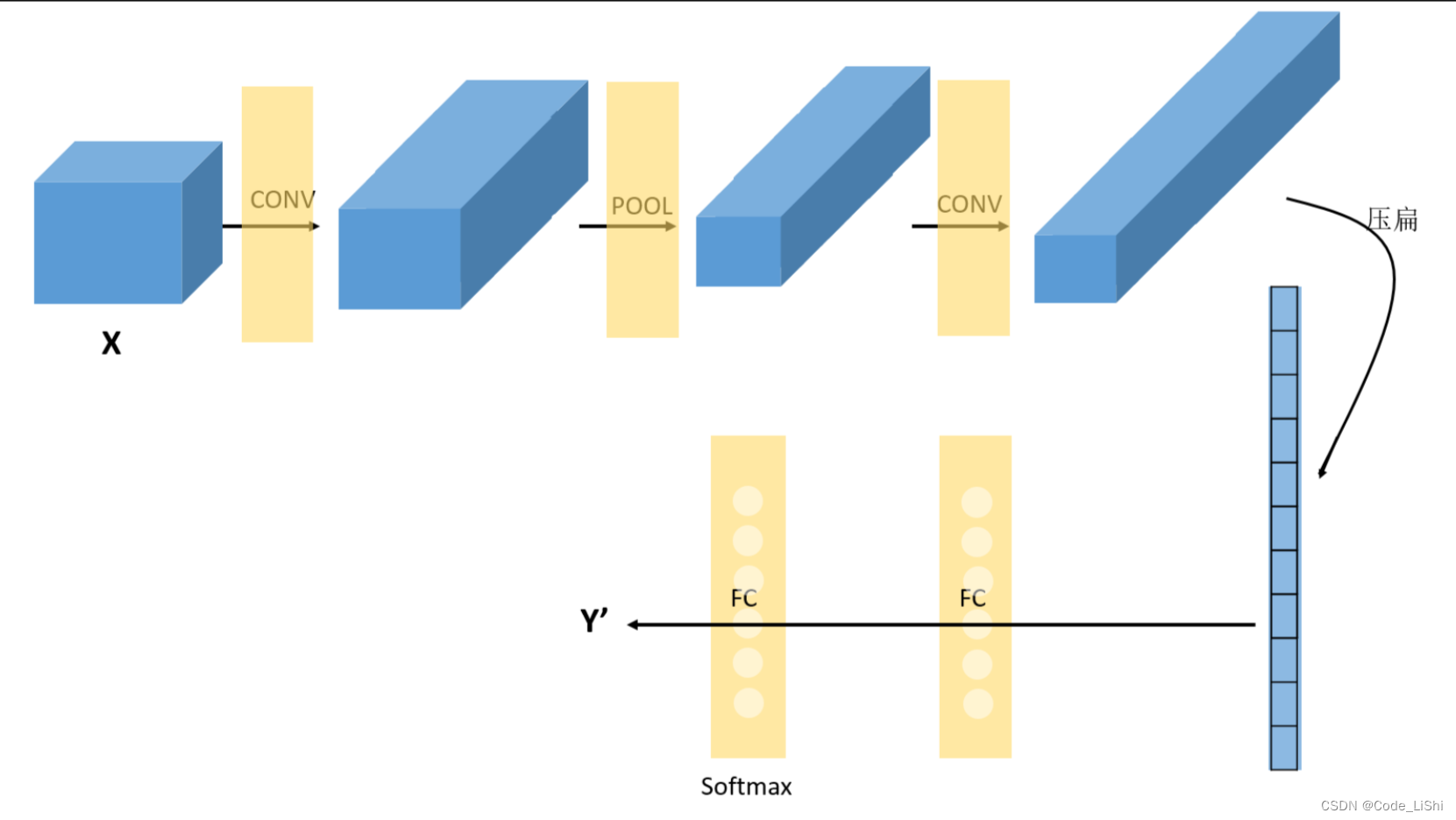
这里需要说明的是,在经过数次卷积和池化之后,我们 最后会先将多维的数据进行“扁平化”,也就是把 (height,width,channel)的数据压缩成长度为 height × width × channel 的一维数组,然后再与 FC层连接,这之后就跟普通的神经网络无异了。
可以从图中看到,随着网络的深入,我们的图像(严格来说中间的那些不能叫图像了,但是为了方便,还是这样说吧)越来越小,但是channels却越来越大了。在图中的表示就是长方体面对我们的面积越来越小,但是长度却越来越长了。卷积神经网络 VS 传统神经网络
其实现在回过头来看,CNN跟我们之前学习的神经网络,也没有很大的差别。
传统的神经网络,其实就是多个FC层叠加起来。
CNN,无非就是把FC改成了CONV和POOL,就是把传统的由一个个神经元组成的layer,变成了由filters组成的layer。
那么,为什么要这样变?有什么好处?
具体说来有两点:1.参数共享机制(parameters sharing)
我们对比一下传统神经网络的层和由filters构成的CONV层:
假设我们的图像是8×8大小,也就是64个像素,假设我们用一个有9个单元的全连接层:
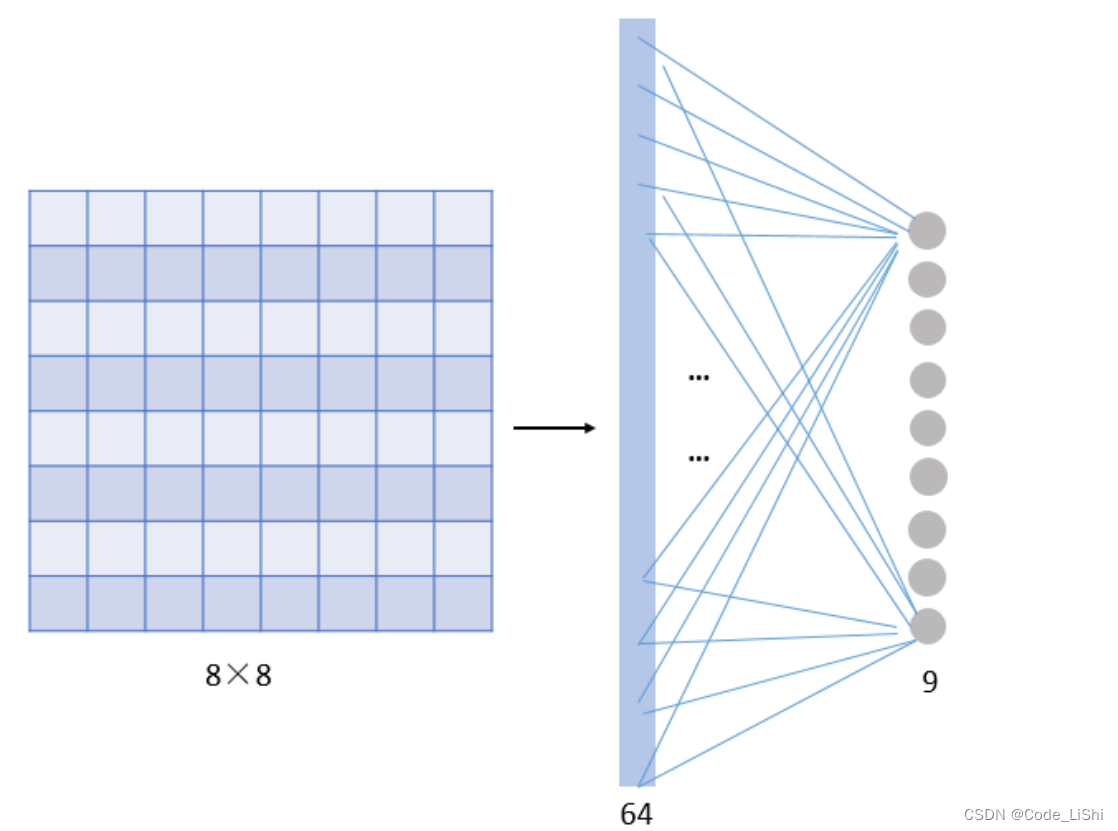
使用全连接那这一层我们需要多少个参数呢?需要 64×9 = 576个参数(先不考虑偏置项b)。因为每一个链接都需要一个权重w。
那我们看看 同样有9个单元的filter是怎么样的:
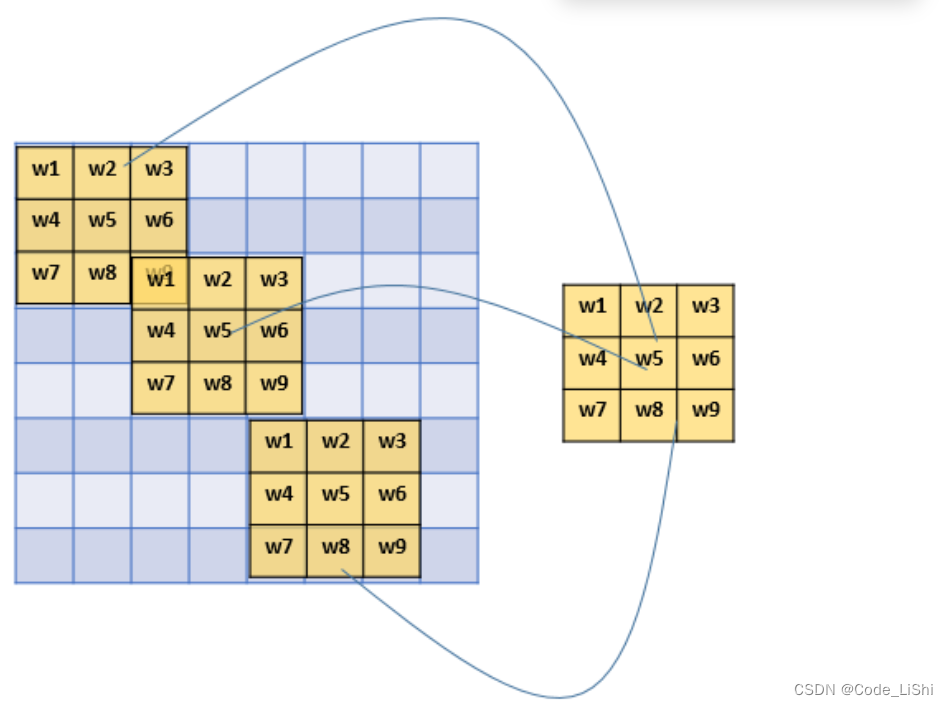
使用filter其实不用看就知道,有几个单元就几个参数,所以总共就9个参数!
因为,对于不同的区域,我们都共享同一个filter,因此就共享这同一组参数。
这也是有道理的,通过前面的讲解我们知道,filter是用来检测特征的,那一个特征一般情况下很可能在不止一个地方出现,比如“竖直边界”,就可能在一幅图中多出出现,那么 我们共享同一个filter不仅是合理的,而且是应该这么做的。由此可见,参数共享机制,让我们的网络的参数数量大大地减少。这样,我们可以用较少的参数,训练出更加好的模型,典型的事半功倍,而且可以有效地 避免过拟合。
同样,由于filter的参数共享,即使图片进行了一定的平移操作,我们照样可以识别出特征,这叫做 “平移不变性”。因此,模型就更加稳健了。2.连接的稀疏性(sparsity of connections)
由卷积的操作可知,输出图像中的任何一个单元,只跟输入图像的一部分有关系:
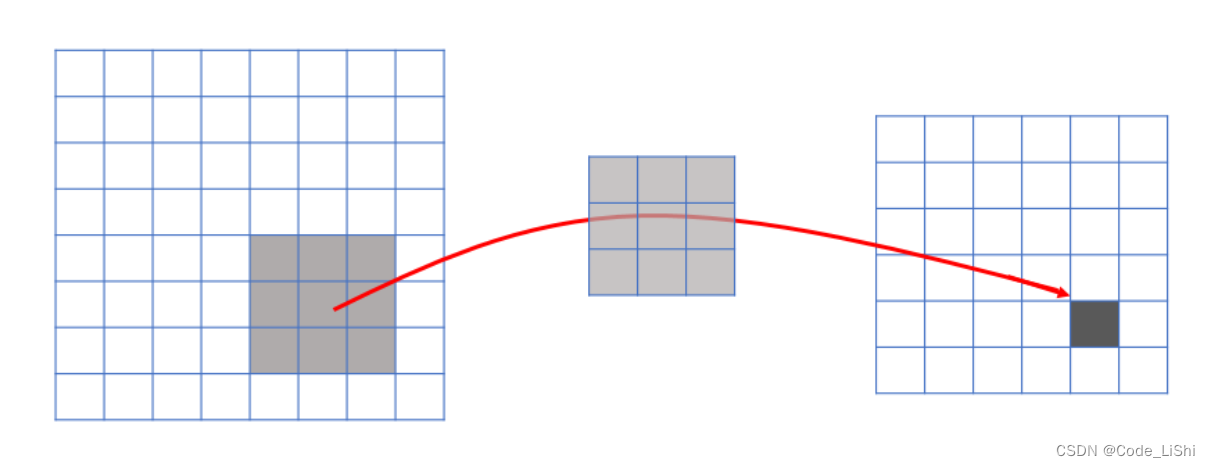
只跟输入的一部分有关而传统神经网络中,由于都是全连接,所以输出的任何一个单元,都要受输入的所有的单元的影响。这样无形中会对图像的识别效果大打折扣。比较,每一个区域都有自己的专属特征,我们不希望它受到其他区域的影响。
正是由于上面这两大优势,使得CNN超越了传统的NN,开启了神经网络的新时代。
-
相关阅读:
正则表达式判断IP地址(python)
Jenkins代理模式配置Maven工程
组件框架网站+demo库+svg库+渐变色库网站+矢量图网站等等
VMware Workstation中桥接模式、NAT模式、仅主机模式
核货宝:选择批发订货系统源码需要注意的三大关键点
面向大规模向量搜索引擎的内存-硬盘优化的近似最近邻搜索算法(GRIP)
C++中的继承
Q&A特辑|重点重点!模型开发与部署的标准答案!
文件操作(下)
黑猫带你学UFS协议栈第3篇:UFSHCI系统框架介绍
- 原文地址:https://blog.csdn.net/weixin_43588171/article/details/134014875