深度学习_5_模型拟合_梯度下降原理

需求:

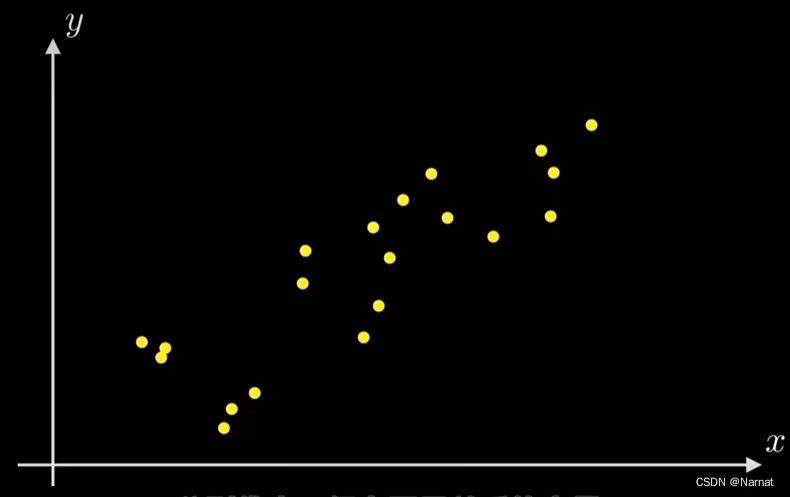
想要找到一条直线，能更好的拟合这一些点

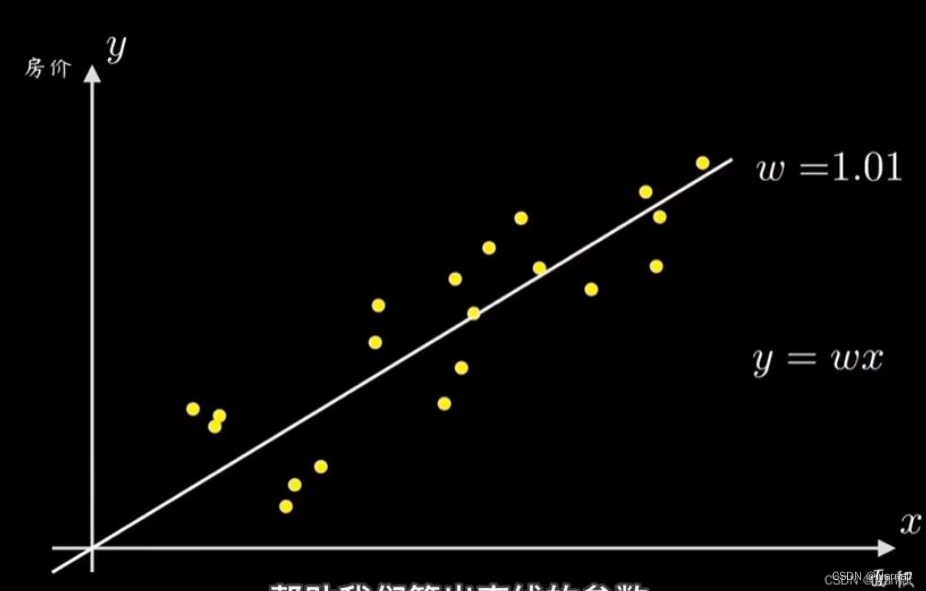
如何确定上述直线就是最优解呢？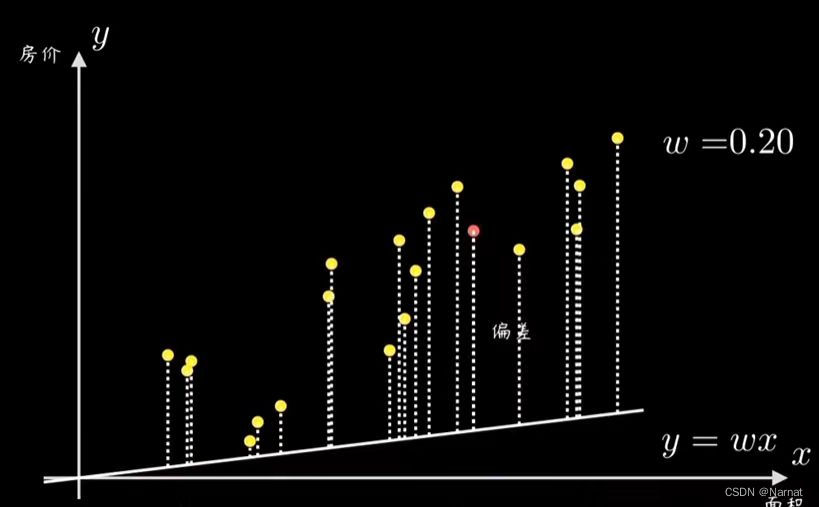

由计算机算出所有点与我们拟合直线的误差，常见的是均方误差

例如：P1与直线之间的误差为e1

将P1坐标带入直线并求误差得：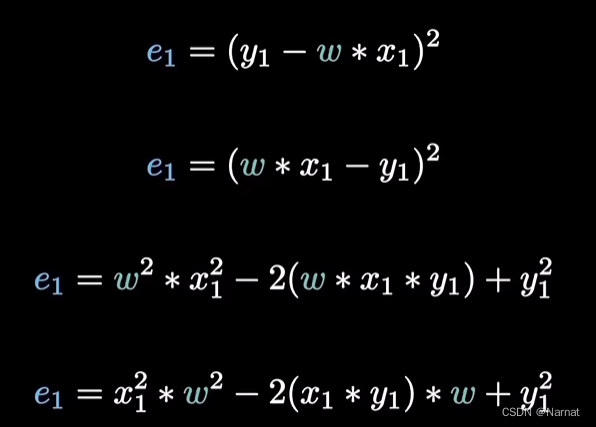

推广到所有点：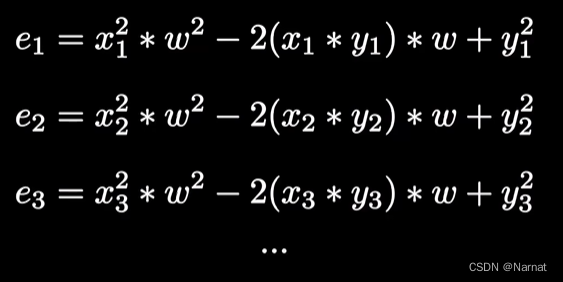

整合：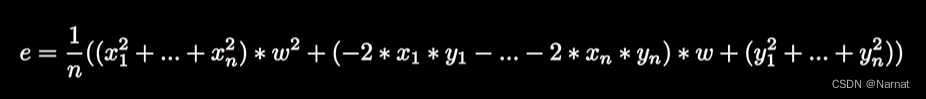

由于xi, yi都为已知点，那么它们就是常数

化简：

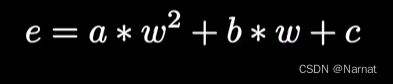
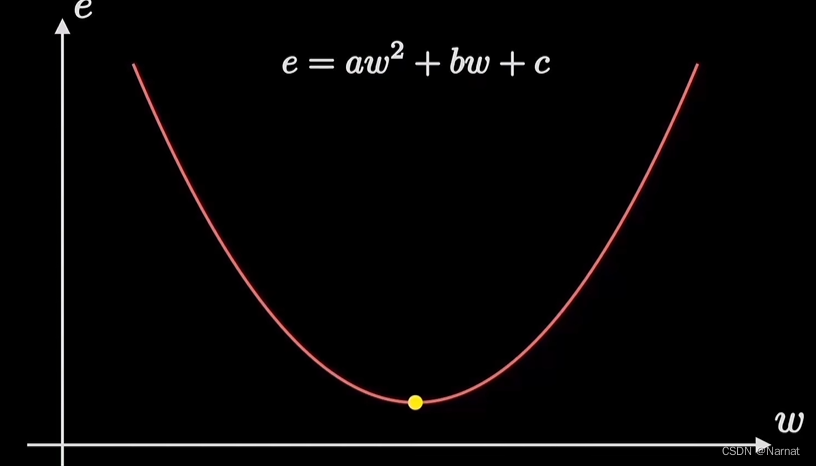
这个误差函数就称为代价函数，其中a, b, c为常数，w为直线得斜率

目标：

找到一个斜率w能使这条直线能更好得拟合上述所有点，反应出来的实质就是e最小

简而言之就是找到一个最优解w0使e最小

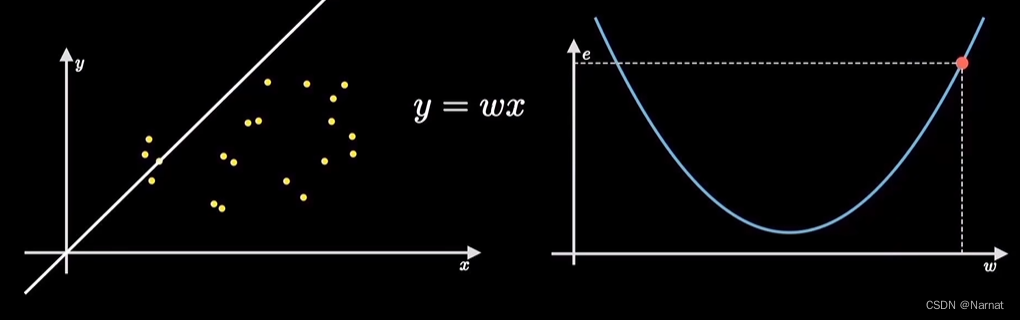
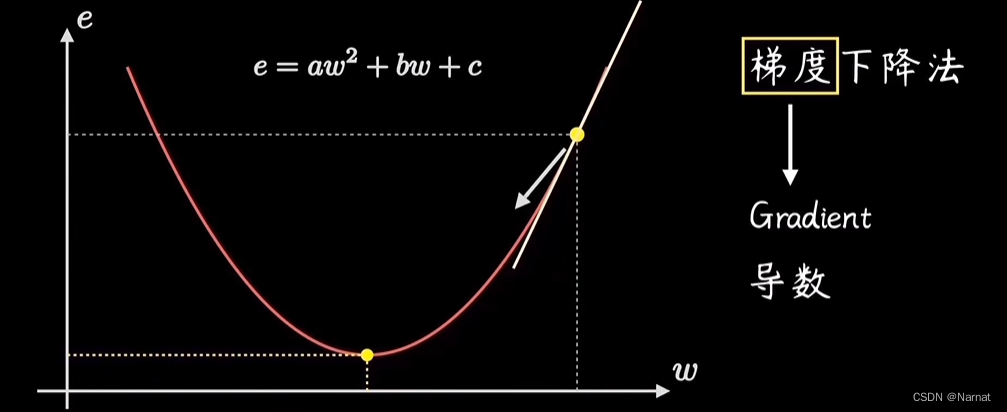
对于最优解w0，当w > w0时w位置所对应导数（也称斜率或梯度）大于零，w < w0时导数小于零

所以为了更好的迭代出最优解，得出以下迭代公式：

等高线大致可以这样理解：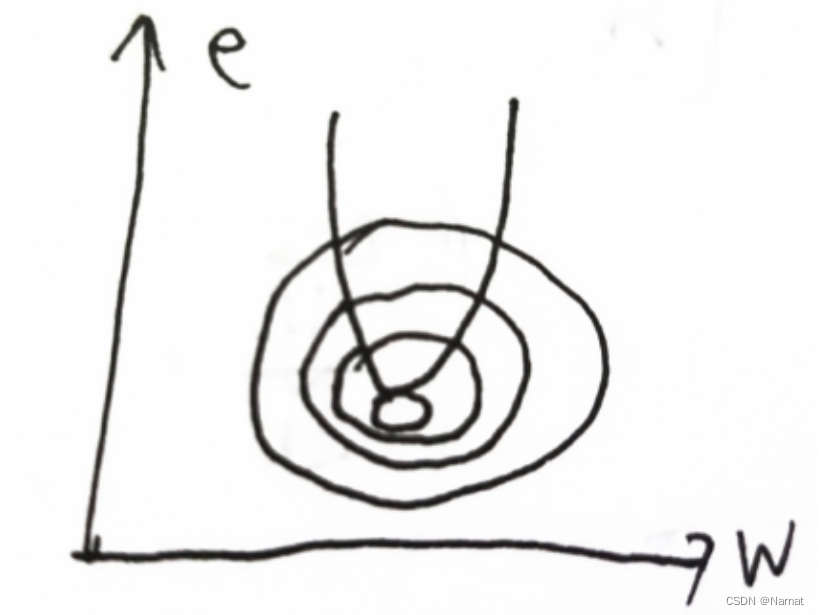

学习率过大过小都不行,太大了下降过快，太小了太慢

为什么不直接用 w = -b/2*a求解？

要拟合这些点，直线就得是y = k * x + b，这可有两个变量

按照上述理论求代价函数为了防止与常数向量表示重复，我用x = k， y = b

最后得到：

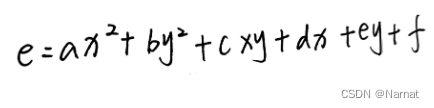
其中a,b,c,d,e,f均为常数

那么此方程就一个三维的了，x = -b/2a也不顶用了

求解过程：

使用梯度下降优化 k 和 b 的基本步骤：

1.初始化 k 和 b 的值。

2.定义损失函数，常见的选择是均方误差（Mean Squared Error）损失函数。
它可以表示为 loss = (1/N) * sum( (y - (kx + b))^2 )，其中 N 是点的数量，y 是真实的 y 值，x 是对应的 x 值。

3.计算损失函数关于 k 和 b 的梯度。这可以通过计算损失函数对 k 和 b 的偏导数来实现。

4.使用梯度下降算法更新 k 和 b。梯度下降的更新规则为 k = k - learning_rate * gradient_k，b = b - learning_rate * gradient_b，其中 learning_rate 是学习率，
gradient_k 和 gradient_b 是损失函数关于 k 和 b 的梯度。

重复步骤 3 和 4，直到达到停止条件（例如达到一定的迭代次数或损失函数的变化小于某个阈值）。
1
2
3
4
5
6
7
8
9
10
11
12
13

计算机会不断得通过这个梯度下降的过程找到最优解x, y，这也就是为什么学习次数达到一定量构建出来的模型也更精确

疑惑：

1、为什么损失函数最小对应的损失函数对k的偏导与损失函数对应b的偏导值趋近于零？

当损失函数对模型参数的偏导数趋近于零时，意味着在该参数值附近，损失函数的变化非常小，再进行参数更新可能不会有明显的改进。这时，我们可以认为模型已经接近局部最优解，损失函数的值也趋近于最小值。

具体来说，对于线性回归模型中的参数 k 和 b，损失函数对 k 的偏导数和对 b
的偏导数的趋近于零表示在当前参数值附近，沿着每个参数的变化方向，损失函数的变化非常小。这可以解释为损失函数对参数的梯度几乎为零，即在该点附近的斜率几乎为零，导致参数不会有太大的变化。

当参数的梯度趋近于零时，梯度下降算法会收敛，即停止参数更新，认为找到了局部最优解或者接近最优解。这是梯度下降算法的终止条件之一。但需要注意的是，梯度下降可能会停在局部最优解而非全局最优解，因此在实际应用中，可以通过调节学习率等参数来控制梯度下降的迭代过程，以更好地找到最优解。

2、什么是局部最优解和全局最优解？

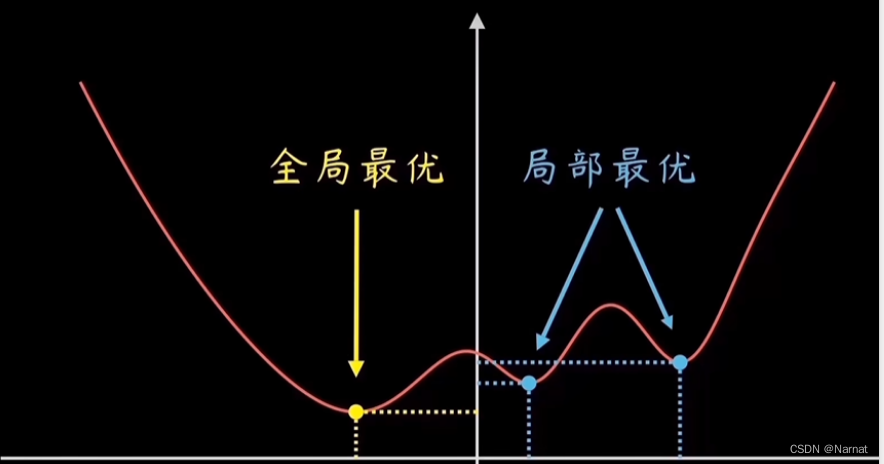
这也正是为什么利用机器学习产生的模型会产生大的误差

3、怎么能确保这个最小值e是全局最小而不是局部最小

为了确保找到的最小值是全局最小而不是局部最小，我们可以采用以下方法：
1、使用随机初始化参数的方法。通过多次运行算法并随机初始化参数，可以增加找到全局最小的概率。
2、调整学习率。如果学习率过大，可能会导致算法在最小值附近震荡而无法收敛到全局最小；如果学习率过小，则算法可能会陷入局部最小。因此，需要适当调整学习率的大小。
3、使用动量法或自适应学习率法等优化算法。这些算法可以在梯度变化缓慢时加速收敛，而在梯度变化剧烈时减小更新幅度，从而避免陷入局部最小。
4、添加正则化项。正则化项可以限制模型的复杂度，防止模型过度拟合训练数据，从而提高模型的泛化能力。同时，正则化项也可以使损失函数更加平滑，减少陷入局部最小的可能性。

学习渠道：梯度下降 & Chatgdp