1.银行家算法

1.1 单资源情况

场景类比

假设银行家手中只有100亿

企业A借20亿，企业B借10亿，企业C借30亿

上表中,银行家已经向三家企业贷款总额达到20+10+30=60亿,目前银行家手中还有100-60=40亿

请求：企业A还想要借30亿，假设我们答应此请求，看看会发生什么？

目前银行家手中还有40-30=10亿,如果此时三家企业中任意一家再向银行家借大于10亿的贷款,那么银行家的钱显然是不够的,这时候我们称作"不安全状态".也就是系统的资源数不能够满足未来的需求,系统处于一种不安全的状态

故上述请求:：企业A还想要借30亿会导致系统处于不安全状态，所以该请求不能够答应
也就是可能会导致进程死锁，

回到上述请求的上一个状态，目前银行家手中有40亿

请求：企业B还想要借20亿

将银行家手中最后剩余的20亿借给企业C，以此满足企业C的最大贷款需求
企业C尽快还回了贷款50亿

目前银行家手中有50亿，将50亿贷款给企业A，以满足企业A的最大需求
企业C尽快还回了贷款70亿

最后银行家将10亿贷款给企业B，以满足企业B的最大需求

企业C尽快还回了贷款40亿

第二阶段贷款顺序为 C $\to$ A $\to$ B，对应着进程向操作系统请求分配资源的顺序，这样的顺序被称为安全序列，即不会造成死锁的进程请求资源的顺序，当然这样的安全序列不唯一

银行家算法的核心思想：每次资源分配前判断此次分配是否会导致系统进入不安全状态，以此来决定是否答应资源分配请求

1.2 多资源情况

1.2.1 银行家算法的整体过程

${\text{Request}}_i$是进程$P_i$的请求向量,向系统申请各类资源的数目组成的向量,该向量小于最大需求和仍需资源数量

①检查此次申请是否超过了之前声明的仍需资源数量

${\text{Request}}_i[j]\le Need[i,j]$

②检查此时系统剩余的可用资源是否还能满足这次请求

${\text{Request}}_i[j]\le \text{Available}[i,j]$

③试探着分配,更改各个数据结构

进程请求资源后,可用资源需要作出更改,减掉进程申请的资源数目
$\text{Available}=\text{Available}-{\text{Request}}_i$

系统为进程$P_i$已经分配的资源数目需要作出更改,加上问系统申请来的资源数目
$\text{Allocation}[i,j]=\text{Allocation}[i,j]-{\text{Request}}_i[j]$
进程$P_i$,第 j-1 类资源

进程$P_i$还需要的资源数目需要作出更改,减去问系统已经申请来的资源数目
$\text{Need}[i,j]=\text{Need}[i,j]-{\text{Request}}_i[j]$

④用安全性算法检查此次分配是否会导致系统进入不安全状态

1.2.2 安全性算法

由原来单个数字表示一类资源，到现在多个数字表示多类资源，将多个数字写成向量的形式，即类似 (资源1,资源2,资源3)，多类资源的话就对应向量的减法

接下来我们需要求安全序列

假设系统中5个进程 ($P_0,P_1,P_2,P_3,P_4$)，三类资源 (A,B,C)，目前各资源可用数量(Available)分别为(10,5,7)

我们设置一个工作向量 Work,用来表示系统中剩余可用资源数目,即表示变化着的 Available
Work 的初始值等于 Available的值,即Work=(3,3,2)

进程对各类资源的最大需求 $-$ 系统已经为进程分配的各类资源数目 $=$ 各进程对各类资源还需要的数目

剩余可用的资源数(Available)或者Work向量 $>$ 仍需资源量(Need)，则系统处于安全状态

$$\begin{gathered} \text{进程P0：}(7,4,3)>(3,3,2)\text{可用资源}\text{,系统不安全} \\ \text{进程P1：}(1,2,2)<(3,3,2)\text{可用资源}\text{,系统安全} \\ \text{进程P2：}(6,0,0)>(3,3,2)\text{可用资源}\text{,系统不安全} \\ \text{进程P3：}(0,1,1)<(3,3,2)\text{可用资源}\text{,系统安全} \end{gathered}$$

进程P1使用资源后释放系统为自己分配的所有资源,故Work需要加上那些已经分配给P1的资源(2,0,0)
进程P1加入安全序列后不再需要系统为其分配资源,所以Need矩阵中删除了P1
安全序列暂时为:{P1}

重复步骤2

$$\begin{gathered} \text{进程P0：}(7,4,3)>(5,3,2)\text{可用资源}\text{,系统不安全} \\ \text{进程P2：}(6,0,0)>(5,3,2)\text{可用资源}\text{,系统不安全} \\ \text{进程P3：}(0,1,1)<(5,3,2)\text{可用资源}\text{,系统安全} \\ \text{进程P4：}(4,3,1)<(5,3,2)\text{可用资源}\text{,系统安全} \end{gathered}$$
进程P3加入安全序列中,等待P3运行完成后释放占用资源,故Work需要加上那些已经分配给P3的资源(2,1,1)
故工作向量Work更新为
$$(5,3,2)+(2,1,1)=(7,4,3)$$
安全序列暂时为:{P1,P3}
需求矩阵Need更新为(去掉了P3的那一行):

重复步骤2

$$\begin{gathered} \text{进程P0：}(7,4,3)=(7,4,3)\text{可用资源}\text{,系统安全} \\ \text{进程P2：}(6,0,0)<(7,4,3)\text{可用资源}\text{,系统安全} \\ \text{进程P4：}(4,3,1)<(7,4,3)\text{可用资源}\text{,系统安全} \end{gathered}$$
进程P4加入安全序列中,等待P4运行完成后释放占用资源,故Work需要加上那些已经分配给P4的资源(0,0,2)

故工作向量Work更新为
$$(7,4,3)+(0,0,2)=(7,4,5)$$
安全序列暂时为:{P1,P3,P4}
需求矩阵Need更新为(去掉了P4的那一行):

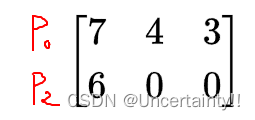
重复步骤2

$$\begin{gathered} \text{进程P0：}(7,4,3)<(7,4,5)\text{可用资源}\text{,系统安全} \\ \text{进程P2：}(6,0,0)<(7,4,5)\text{可用资源}\text{,系统安全} \end{gathered}$$
安全序列暂时为:{P1,P3,P4,P2}
进程P2加入安全序列中,等待P2运行完成后释放占用资源,故Work需要加上那些已经分配给P2的资源(3,0,2)
故工作向量Work更新为
$$(7,4,5)+(3,0,2)=(10,4,7)$$
安全序列暂时为:{P1,P3,P4,P2}
需求矩阵Need更新为(去掉了P2的那一行):

重复步骤2

$$\text{进程P0：}(7,4,3)<(10,4,7)\text{可用资源}\text{,系统安全}$$
安全序列最终为:{P1,P3,P4,P2,P0}

安全性算法是银行家算法的最重要步骤

1.2.3 分配资源

每个进程都会向系统发送请求向量,系统根据此请求向量进行安全性检查,得到一个安全序列,而后系统仅会为此进程分配资源,其他进程仍需向系统发送请求向量,重复以上过程