一起学数据结构（11）——快速排序及其优化

     上篇文章中，解释了插入排序、希尔排序、冒泡排序、堆排序及选择排序的原理及具体代码实现本片文章将针对快速排序，快速排序的几种优化方法、快速排序的非递归进行解释。

目录

1. 快速排序原理解析以及代码实现：

2. 如何保证相遇位置的值一定小于所对应的值：

3 优化最坏情况下快速排序的时间复杂度：

4. 对于快速排序代码书写格式的优化（挖坑法）：

5. 对于快速排序代码的另一种书写格式优化（前后指针法）： 

---

1. 快速排序原理解析以及代码实现：

给定下面一个数组：

       对于快速排序，其中心思想就是首先选取一个值，一般选择数组中最左边的数据，例如本数组中的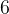。创建一个变量，来保存这个值所对应的下标，为了方便表达，将这个变量命名为。

      在确定了之后，分别从两头遍历数组，定义两个变量用于遍历数组，其中，，。

     对于遍历数组的过程，需要分成两种情况来查看。其中，用于从左向右遍历数组，用于从右向左遍历数组。当数组从左向右进行遍历时，一旦遇到比所对应的值大的数据，则停在这个数据的所对应的下标处。即：

当数组从右向左进行遍历时，一旦遇到比所对应的值小的数据，则停在这个数据的所对应的下标处。即：

在找到了符合上面规定的值后，交换两个值在数组中的位置：

接着继续向下遍历，并且重复之前的动作。当，相遇时，停止循环，此时的数组可以表示为：

最后，将所对应的值，与此时或者所对应的值进行一次交换，便完成了整个流程，用图形表示为：

 在进行了上面一整套流程后，此时的数组虽然还是无序，但是可以观察到，所对应的值的右半部分的数组的值都大于所对应的值。左半部分数组的值都小于所对应的值。

对于上述流程，可以用下面的代码进行表示：

 //部分快排
 int PortSort(int* a, int left, int right)
 {
	 int key = left;
	 while (left < right)
	 {
		 //先从右边开始找小的
		 while( left < right && a[right] >= a[key])
		 {
			 right--;
		 }
 
		 //再从左边开始找大的
		 while(left < right && a[left] <= a[key])
		 {
			 left++;
		 }
 
		 //交换找到的值
		 Swap(&a[left], &a[right]);
	 }
	 Swap(&a[key], &a[left]);
 
	 return left;
 }

对于上述给出的代码中，需要注意两个点：

1.在进行遍历数组寻找值的时候，必须先从右边开始遍历找小于所对应的值的数据，再从左边找大于所对应的值的数据，对于原因将会在文章的后面进行探讨

2.在遍历寻找值的循环中，需要注意循环的两个条件，即并且，前面的条件是为了防止下面的两种情况：若从左向右遍历时，不存在比对应的值大的数据，从右向左遍历时，不存在比对应的值小的数据。以上两种情况均会导致的范围超出数组下标的范围，对于第二个条件，如果不加上，一旦在遍历的过程中，遇到了与对应的值相等的值，会造成死循环。   

       完成了上述步骤后，数组依然是无序的，为了处理数组中其他的数据，需要利用到类似二叉树中递归的思想来实现：

       对于上述数组，他的数组左半部分的数据都是小于所对应的值的，对于数组的右半部分的数据都是大于所对应的值的，因此在下面的递归中，需要以为分界线，的左半部分为一组，右半部分为一组，对这两组值再次进行一次上面给出代码所对应的操作。

     例如，对于左半部分：

此时所对应的值为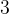，按照上述代码进行操作后，数组可以表示为：

随后，再以为分界线，分出左右部分，对于左右部分进行上述代码的操作，对于左半部分，进行一次操作后，可以表示为：

       此时，再向下进行递归，的左半区间不存在，的右半区间只有一个值。因此，对于上面两种情况，视作递归结束的条件。

      上面只是展示了每一次的递归中，数组的左半部分的情况，对于右半部分原理相同，这里不再进行赘述。当作伴部分，右半部分的递归都结束后，整个区间会变成有序的区间，即：

对于上述递归，可以用下列代码进行实现：

 void QuickSort(int* a, int begin, int end)
 {
	 if (begin >= end)
		 return;
 
	 int keyi = PortSort(a, begin, end);
 
	 QuickSort(a, begin, keyi - 1);
	 QuickSort(a, keyi + 1, end);
 }

测试函数如下：

void TestQuickSort()
{
	int e[] = { 6,1,2,7,9,3,4,5,10,8 };
	int size = sizeof(e) / sizeof(int);
	QuickSort(e, 0,size-1);
	printf("快速排序：");
	ArrayPrint(e, size);
}

结果如下：

2. 如何保证相遇位置的值一定小于所对应的值：

       上面说到，在进行遍历寻找值这一步骤时，一定要先从右边开始向左遍历来找到比对应的值小的值，再从左边向右开始遍历，来寻找比对应值大的值，原因如下：

例如对于上面给出的数组，对于相遇的前一步情况：

假设左边先进行遍历去寻找值，再从右边向左遍历来寻找值，则二者相遇的位置为：

此时，如果按照上面代码的内容对对应的值和位置对应的值进行交换，则：

此时，比对应的值大的值不只是只存在右边。 

这里需要注意，先从右边往左边遍历的，对应的是的位置在数组的左端。当在数组的右端时，需要先从左边向右遍历。

3 优化最坏情况下快速排序的时间复杂度：

快速排序的时间复杂度一般都认为是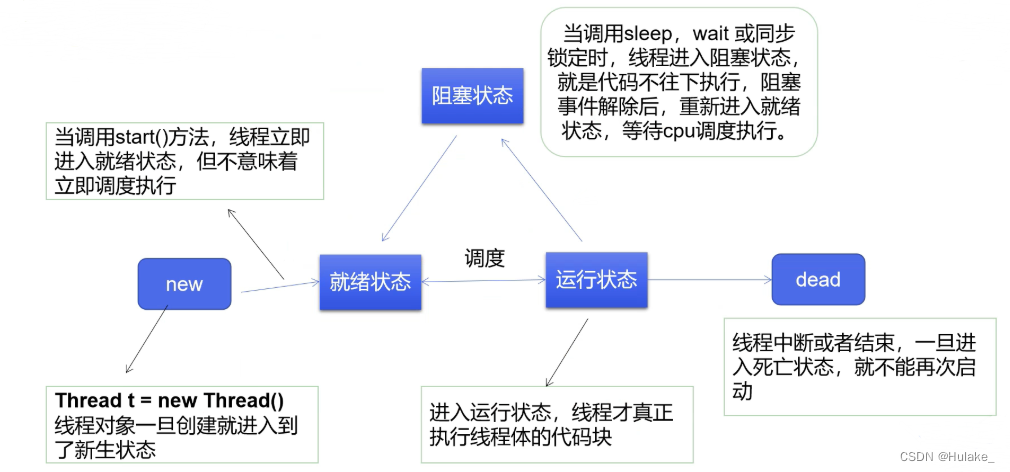，但是对于下面的一种情况：

前面说到，在快速排序中，当取左端的值时，应该优先从右边开始遍历，对于例子中这种完全升序，或者说大部分区间都是升序的情况，每次从右端进行遍历时，都必须遍历到数组的最左边。因此，对于一个有个数据的这样的数组来说，从右向左遍历的次数为次，这种情况下的快速排序的时间复杂度为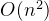。为了优化这种情况，这里引入三数取中的方法。代码如下：因为原理就是简单的两数相比，所以不做过多解释：

 //三数取中
 int GetMidi(int* a, int left, int right)
 {
	 int mid = (left + right) / 2;
	 if (a[left] < a[mid])
	 {
		 if (a[right] > a[mid])
		 {
			 return mid;
		 }
		 else if (a[left] > a[right])
		 {
			 return left;
		 }
		 else
		 {
			 return right;
		 }
	 }
	 else//(a[left] > a[mid];
	 {
		 if (a[mid] > a[right])
		 {
			 return mid;
		 }
		 else if (a[left] < a[right])
		 {
			 return left;
		 }
		 else
		 {
			 return right;
		 }
	 }
 }

 在构建了三数取中函数之后，需要对之前的快速排序代码进行修改。修改的部分为：首先在函数的开头创建一个变量用于接受三数取中函数的返回值。接着，让对应的数值与后续下标对应的数据（即最左端，或者最右端）用交换函数交换即可。

4. 对于快速排序代码书写格式的优化（挖坑法）：

对于挖坑法，具体的实现原理如下：

首先还是确认以及所对应的值，例如在下面的例子中

（注：为了方便演示原理，下面的情况不包括三数取中，但是在书写代码时，使用三数取中的方法与上方的使用发放相同）

       首先确定一个，这里按照左端处理，创建一个变量，令，接着，确定所在的下标就是第一个坑位。在确认了第一个坑位后，与上面的快速排序相同，都需要先从右端开始遍历来找到比小的值，即：

随后，直接让所指向的值覆盖到的位置，再让指向的位置变成新的坑，即：

 再从左边向右进行遍历，找到比小的值，并且让这个值覆盖到坑位中，再令下图中的成为新的坑位：

 继续从右向左进行遍历，再从左向右遍历，直到相遇为止，即：

最后，再令二者相遇的位置赋值即可。然后再按照上面的思想递归即可。代码实现为：
 

//快排优化(挖坑法）
 int QuickDigSort(int* a, int begin, int end)
 {
	 int mid = GetMidi(a, begin, end);
	 Swap(&a[begin], &a[mid]);
	 int key = a[begin];
	 int hole = begin;
	 while (begin < end)
	 {
		 //先从右边开始找小的
		 while (begin < end && a[end] >= key)
		 {
			 end--;
		 }
		 a[hole] = a[end];
		 hole = end;
		 //再从左边开始找大的
		 while (begin < end && a[begin] <= key)
		 {
			 begin++;
		 }
		 a[hole] = a[begin];
		 hole = begin; 
	 }
	 a[hole] = key;
	 return hole;	
 }
 
void QuickSort2(int* a, int begin, int end)
 {
	 if (begin >= end)
		 return;
 
	 int keyi = QuickDigSort(a, begin, end);
 
	 QuickSort2(a, begin, keyi - 1);
	 QuickSort2(a, keyi + 1, end);
 }

测试函数如下：

void TestQuickDigSort()
{
	int f[] = { 6,1,5,3,9,10,7,4,2,8 };
	int size = sizeof(f) / sizeof(int);
	QuickSort2(f, 0, size - 1);
	printf("快速排序(挖坑法)：");
	ArrayPrint(f, size);
}

运行结果如下：

5. 对于快速排序代码的另一种书写格式优化（前后指针法）： 

        对于前后指针法，就是通过控制两个指针，这里分别命名为,。通过控制这两个指针的动作时序来完成对于数组的排序，中心思想如下：

       对于指针的作用，就是用来寻找比小的值（ 的意义与上面相同），对于指针的动作时序，分为下面两种情况： 当没有遇到比大的值时，一直紧跟着，当遇到比大的值后，令的位置处于这个值的前面。

       继续令向后遍历，如果又找到了比小的值，则交换这个值，与后面的值。

例如对于下面的数组：

按照上面所说的思想，在没有遇到比大的值时，一直紧跟着运动，即：

此时，再向下运动，遇到了比大的值，令继续向后遍历，直至找到比小的值，令停在比大的值的前面，即：

再向下运动后，遇到了比小的值，令后面的值与比小的值交换，即：

接着继续向下遍历，此时指向的位置为：

此时再对两个指针指向的值进行交换，即：

在遍历结束时，数组如下：

 在结束遍历后，交换位置的值与的值，即：

交换完后，比小的值都位于左边，比 大的值都位于右边。

总览上面的整个过程，当遇到了比大的值后，两个指针便开始拉开差距。此时每次向后遍历，都会找到一个比大的值，并且形成一个比大的值的区间，在其期间，一直保持不动，直到遇到一个小的值，在向后指向第一个比大的值并且交换，此后每找到一个小的值，都会把之前大的值置换到后面，把小的值置换到前面。

代码如下：

 //快速排序(前后指针法)
 int QuickTailSort(int* a, int begin, int end)
 {
	 int key = begin;
	 int prev = begin, cur = begin+1;
	 while (cur <= end)
	 {
		 if (a[cur] < a[key])
		 {
			 Swap(&a[++prev], &a[cur]);
		 }
			 cur++;;
	 }
	 Swap(&a[key], &a[prev]);
	 return prev;
 }

测试函数如下：

void TestQuickTailSort()
{
	int g[] = { 5,1,6,9,3,10,4,7,2,8 };
	int size = sizeof(g) / sizeof(int);
	QuickSort3(g, 0, size - 1);
	printf("快速排序(挖坑法)：");
	ArrayPrint(g, size);
}

运行结果如下：

6. 快速排序的非递归实现： 

       对于上述的递归方式是借助了二叉树的思想实现的，对于递归来说，一旦需要处理的数据过多，导致递归的深度过多，很有可能会导致栈溢出。所以，对于快速排序的非递归写法的掌握是十分必要的。具体思路如下：

        在前面的递归中，每次递归都是会选取整个数组中一部分区间进行排序。所以，对于区间的存储，是需要第一个解决的问题。文章本处选择使用栈来存储需要排序的区间，具体思路如下：

给定一个数组，其数组的内容以及下标如图所示：

栈如图所示：

 首先，将数组最左边的下标和最右边的下标压入栈，即：

此时，将这两个元素取出，并且按照此范围进行一次快速排序（只是单次处理，不需要递归）的处理，定义接受快速排序的返回值，并且按照,将数组划分为两个区间，再次将这两个区间的左右端下标压入栈，随后重复上述过程，代码表示为：
 

 //快速排序(非递归)
 void QuickSortNonR(int* a, int begin, int end)
 {
	 ST st;
	 STInit(&st);
 
	 //先将最左，最右两端的下标压入栈
	 //注意顺序，后进先出
	 STPush(&st, end);
	 STPush(&st, begin);
 
	 while (!STEmpty(&st))
	 {
		 //取出这两个压入栈的元素
		 int left = STTop(&st);
		 STPop(&st);
 
		 int right = STTop(&st);
		 STPop(&st);
 
		 int keyi = QuickDigSort(a, left, right);
 
		 if (keyi + 1 < right)
		 {
			 STPush(&st, right);
			 STPush(&st, keyi + 1);
		 }
 
		 if (left < keyi - 1)
		 {
			 STPush(&st, keyi - 1);
			 STPush(&st, left);
		 }
	 }
	 STDestory(&st);
 }

测试函数为：

void TestQuickSortNonR()
{
	int h[] = { 10,1,9,5,7,3,4,2,8,6 };
	int size = sizeof(h) / sizeof(int);
	QuickSortNonR(h, 0, size - 1);
	printf("快速排序(非递归)：");
	ArrayPrint(h, size);
}

运行结果为：