17.Tensor Product Spaces

同样，本文仍采用非标准 的符号。

在之前的文章里，已经展示了： 使用张量积将向量和协向量组合在一起可以为我们提供线性映射，这个线性映射的系数实际上只是一个数组的条目。

还展示了：使用张量积组合两个协向量，可以得到一个双线性形式，该双线性形式的系数实际上只是与这些协向量关联的两个行向量的Kronecker 积 给出的数组的条目。

 

张量积是什么

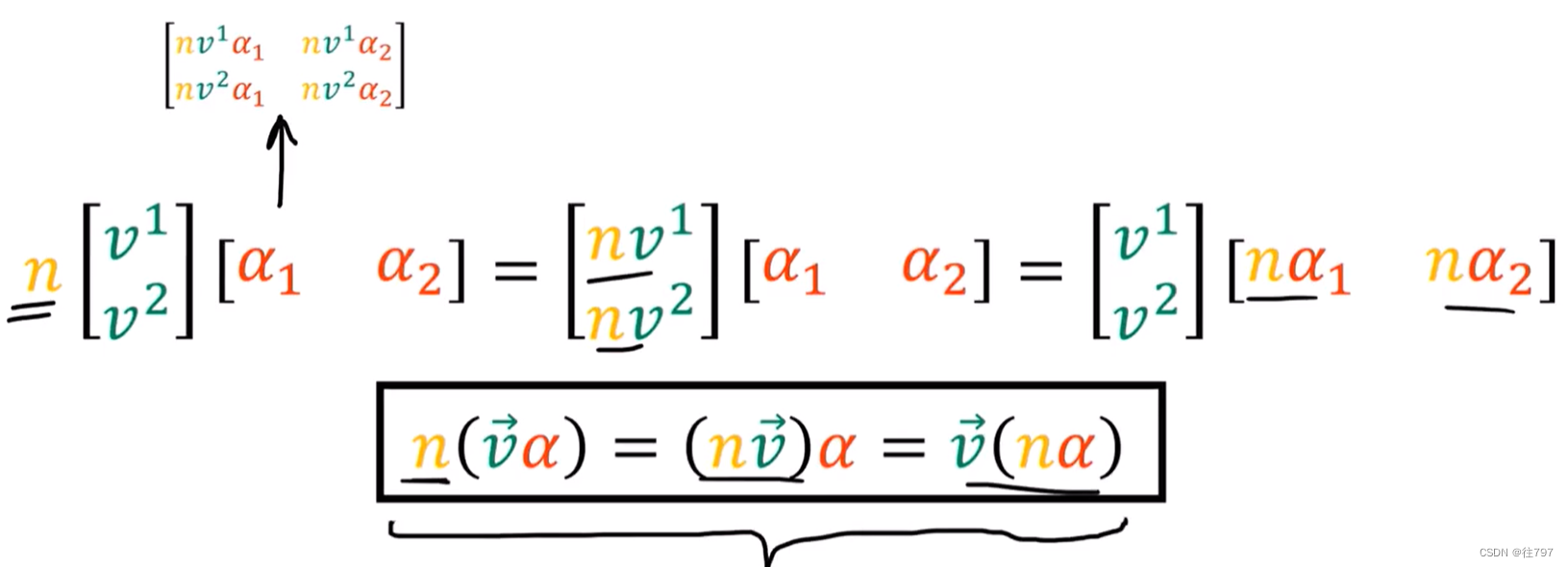
向量和协向量之间的张量积，它按某个数字“n”缩放时，可以按“n”缩放向量或按“n”缩放协向量，都得到相同的结果。

使用标准符号的话，如下图1

加法：

类似于提公因子，并且是在同一侧的。

使用标准符号的话，如下图2：

 

缩放规则其实是：

加法规则：（需要注意的是，必须是公因子在同一侧）

 

张量积空间的概念

有了上面这些规则，它们其实是构成了向量空间

V⨂V∗V⨂V∗是组合了向量空间 ， 不像α⨂⨂β是向量组合向量

what are the elements of V⨂V∗

这个向量空间(V⨂V∗)的成员：（1，1)-Tensors 

记住： 向量分量vi 有个在上方的索引 ； 协向量分量αi 有个在下方的索引。

所以向量空间V⨂V∗的元素可以被解释为任何上图中的东西，这取决于我们给定的输入的数量和类型。

考虑回之前的事情，我们对张量积有相同的旧规则，

V就代表向量空间--分量是上标、向量是下标，  V∗ 就代表协向量空间--分量是下标、协向量是上标， 用⨂作运算的话，就是组合，一个V就一个上标，就这么个规律。

因此，如果我们从以前从未见过的向量空间中获得一些新的张量，只需查看向量空间就可以轻松获得正确的分量索引。

对于所有这些映射都是线性的，如果我选择保持除一个之外的全部输入不变(仅改变一个输入，其他输入不变)， 我们称以这种方式运行的函数为“多线性映射”。

多线性映射  是一个函数，且遵守两个属性：

总结：

了解了张量积的定义，这是一种组合张量的方式，遵循缩放和相加规则。

从张量积中得到的张量形成了新的向量空间，使用向量空间的张量积来表示：

所有的张量都是多线性映射，