【LeetCode】94. 二叉树的中序遍历 [ 左子树 根结点 右子树 ]

题目链接

Python3

方法一： 递归 $⟮O(n)⟯$

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        """中序遍历 [ 左子树 根 右子树 ]： 递归"""
        def inorder(node):
            if not node:
                return 
            inorder(node.left) # 左子树
            ans.append(node.val) ## 根
            inorder(node.right) # 右子树

        ans = []
        inorder(root)
        return ans   
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

方法二： 迭代 $⟮O(n)⟯$

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        """中序遍历 [ 左子树 根 右子树 ]： 迭代"""

        ans = []
        stack = []
        
        cur = root
        while cur or stack:  # 还有结点 未遍历
            while cur:
                stack.append(cur)   
                cur = cur.left  # 左 
            
            ## 开始 出栈 处理         
            cur = stack.pop() # 
            ans.append(cur.val)  # 根
            cur = cur.right  #  右 

        return ans 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

方法三： Morris $⟮O(n)、O(1)⟯$

参考链接

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        """中序遍历 [ 左子树  根  右子树 ]  Morris  O(N) O(1)"""
        ans = []
        cur, pre = root, None 
        while cur:
            if not cur.left:
                ans.append(cur.val)  ##  
                cur = cur.right 

            # 有左孩子
            else:
                # 找 pre 
                pre = cur.left 
                while pre.right and pre.right != cur:
                    pre = pre.right  
                if not pre.right:
                    pre.right = cur
                    cur = cur.left 
                else:
                    pre.right = None 
                    ans.append(cur.val)
                    cur = cur.right 
        return ans 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

C++

方法一： 递归 $⟮O(n)⟯$

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 子模块
    void inorder(TreeNode* node, vector<int> &ans){
        if (node == nullptr){
            return ;
        }
        inorder(node->left, ans);
        ans.emplace_back(node->val);
        inorder(node->right, ans);
    }

    // 主模块
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        inorder(root, ans);
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

方法二： 迭代 $⟮O(n)⟯$

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        if (root == nullptr){
            return ans;
        }

        stack<TreeNode*> stk;
        TreeNode* cur = root;
        while (cur != nullptr || !stk.empty()){
            while (cur != nullptr){
                stk.emplace(cur);
                cur = cur->left; // 左
            }

            cur = stk.top();
            stk.pop();
            ans.emplace_back(cur->val); // 根
            cur = cur->right; // 右
        }

        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

方法三： Morris $⟮O(n)、O(1)⟯$

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        TreeNode* cur = root;
        TreeNode* pre = nullptr;

        while (cur != nullptr){
            if (cur->left == nullptr){// 左子树 遍历完了
                ans.emplace_back(cur->val);  //
                cur = cur->right;
            }
            else{
                // 找 pre 
                pre = cur->left;
                while (pre->right != nullptr && pre->right != cur){
                    pre = pre->right;
                }
                if (pre->right == nullptr){
                    pre->right = cur;
                    cur = cur->left;
                }
                else{
                    pre->right = nullptr;
                    ans.emplace_back(cur->val);  //
                    cur = cur->right; // 右
                }

            }
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

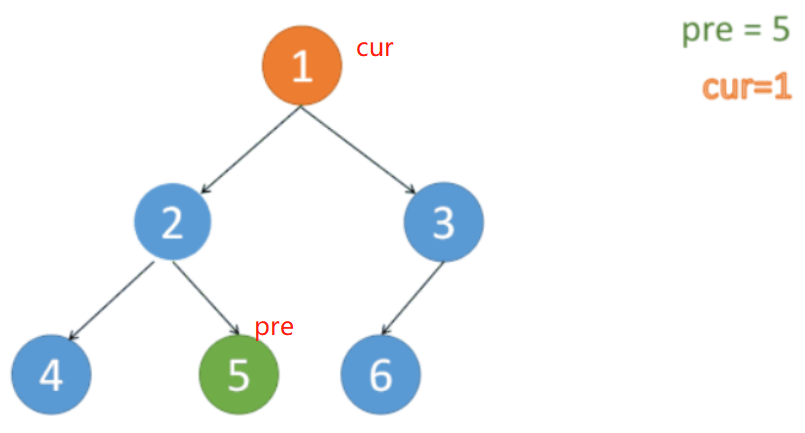
Morris 中序遍历 理解

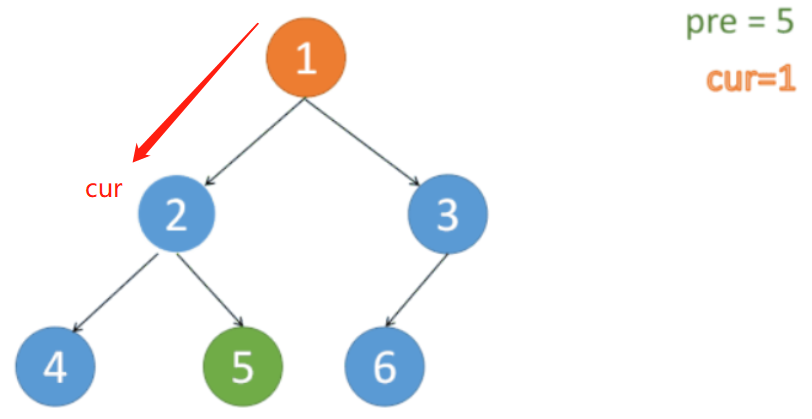
Step 2:
cur 移到 原树 cur 的左结点
原树：

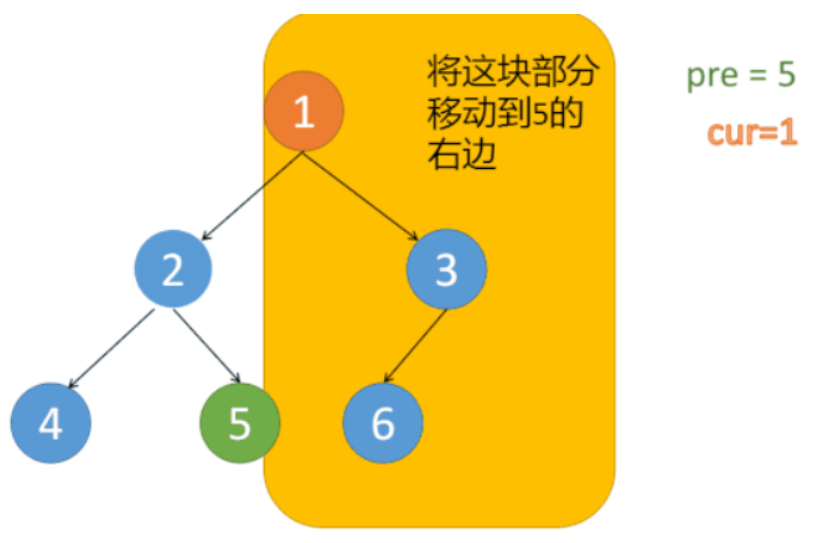
经过 step 1 操作的树

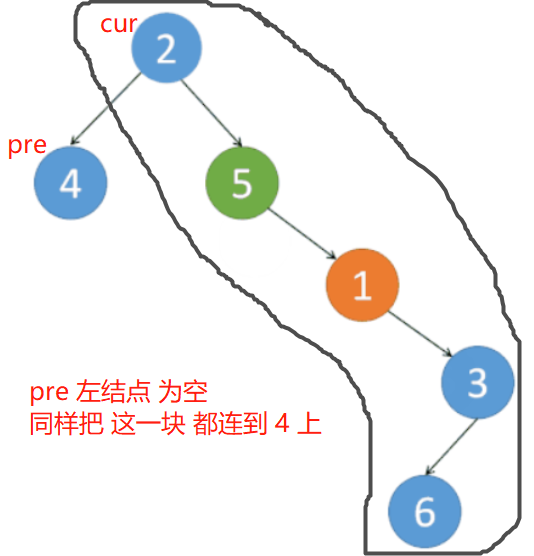
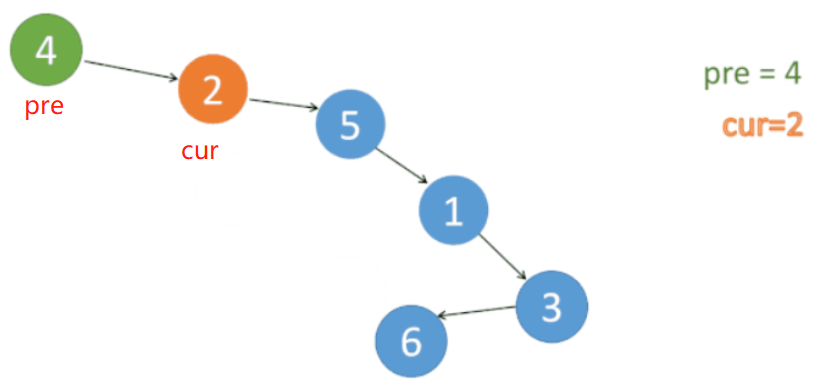
Step 3:

原树：

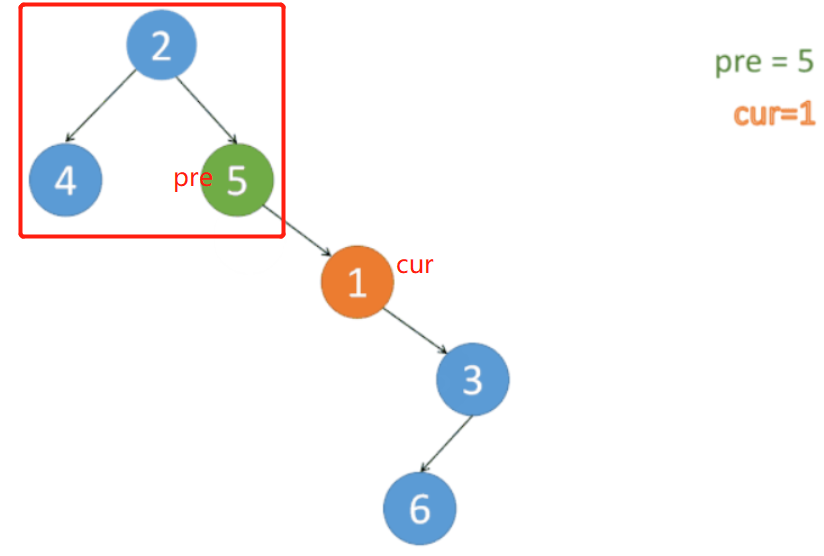
经过 step 2 操作的树

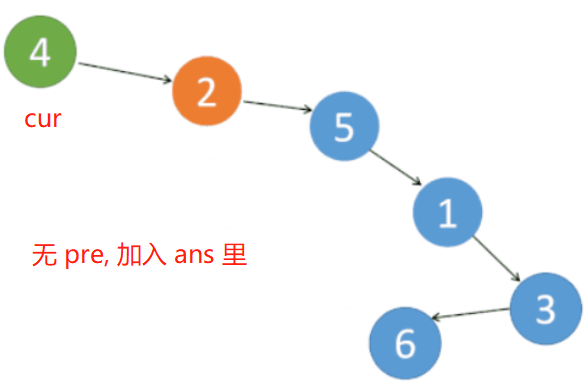
开始 有结点 加入答案里，意味着 原树最左侧的结点 遍历完成。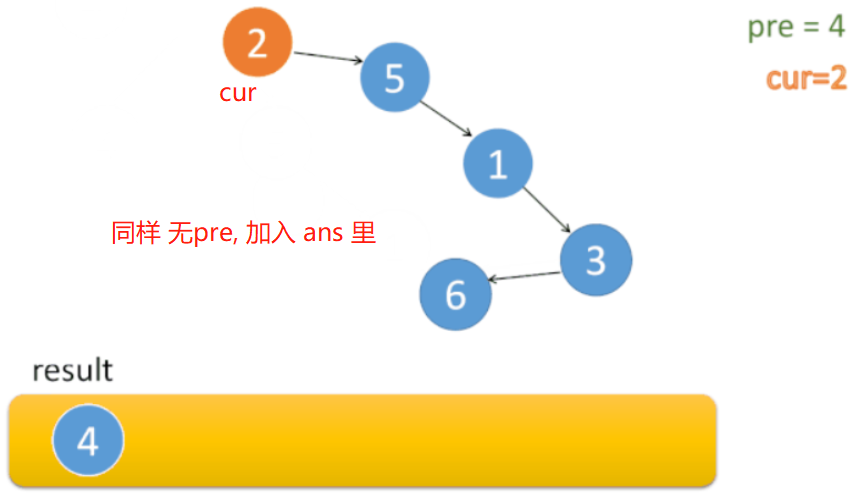

结点 4、2、5、1 依次加到 ans 里。

到 结点 3。 发现 结点 3 有 pre。
则同样 先把 cur及右子树 都加到 pre 的右边。
先处理 左边。


总体思想: 左 根 右
一般先知道 root。
把 root 及其右子树 都 接在 pre【即左子树的 mostright】 后面
处理 左子树。
这样 后面 加 答案 就是 左 根 右 的 顺序。