使用Java语言深度探索数据结构中的递归：完美结合详解与示例代码

版本说明

当前版本号[20231020]。

目录

2.3 递归

1) 概述

定义

计算机科学中，递归是一种解决计算问题的方法，其中解决方案取决于同一类问题的更小子集。

比如单链表递归遍历的例子：

void f(Node node) {
    if(node == null) {
        return;
    }
    println("before:" + node.value)
    f(node.next);
    println("after:" + node.value)
}
1
2
3
4
5
6
7
8

说明：

1. 自己调用自己，如果说每个函数对应着一种解决方案，自己调用自己意味着解决方案是一样的（有规律的）
2. 每次调用，函数处理的数据会较上次缩减（子集），而且最后会缩减至无需继续递归
3. 内层函数调用（子集处理）完成，外层函数才能算调用完成

原理

假设链表中有 3 个节点，value 分别为 1，2，3，null ，以上代码的执行流程就类似于下面的伪码

（以下演示为伪代码演示，不必太在乎语法是否正确）

原来的代码为：

void f(Node node) {
        if (node == null) {
            return;
        }
        println("before:" + node.value); // 打印当前节点的值
        f(node.next); // 递归调用函数，传入下一个节点作为参数
        println("after:" + node.value); // 打印当前节点的值（在递归返回后）
    }
1
2
3
4
5
6
7
8

现在要添加 3 个节点，首先是添加1

• 由于node = 1 不为0，所以if判断node == null 可以整个去掉了，然后继续往下执行
• 打印出当前节点的值
• 开始递归地调用函数，此时就可以把 2 添加进来，重新调用 f 函数，后面的 after 就无需打印了

 void f(Node node = 1) {
       /* if (node == null) {
            return;
        }*/
        println("before:" + node.value); // 打印当前节点的值
        f(node.next); // 递归调用函数，传入下一个节点作为参数
        //println("after:" + node.value); // 打印当前节点的值（在递归返回后）
    }
1
2
3
4
5
6
7
8

现在开始添加2

• 调用 f 函数完后，继续判断。node = 2 不为0，所以if判断node == null 可以整个去掉了，然后继续往下执行
• 打印出当前节点的值
• 开始递归地调用函数，此时就可以把 3 添加进来，重新调用 f 函数，后面的 after 就无需打印了

 void f(Node node = 1) {
       /* if (node == null) {
            return;
        }*/
        println("before:" + node.value); // 打印当前节点的值
          void f(Node node = 2) {
                 /* if (node == null) {
            	    return;
                 }*/
            println("before:" + node.value); // 打印当前节点的值
            f(node.next); // 递归调用函数，传入下一个节点作为参数
            //println("after:" + node.value); // 打印当前节点的值（在递归返回后）
        }
        //println("after:" + node.value); // 打印当前节点的值（在递归返回后）
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

现在开始添加3

• 调用 f 函数完后，继续判断。node = 3 不为0，所以if判断node == null 可以整个去掉了，然后继续往下执行
• 打印出当前节点的值
• 开始递归地调用函数，此时就可以把 null 添加进来，重新调用 f 函数，后面的 after 就无需打印了

 void f(Node node = 1) {
       /* if (node == null) {
            return;
        }*/
        println("before:" + node.value); // 打印当前节点的值
          void f(Node node = 2) {
                 /* if (node == null) {
            	    return;
                 }*/
            println("before:" + node.value); // 打印当前节点的值
                 void f(Node node = 3) {
              	  //if (node == null) {
                  	  return;
             	  // }
                println("before:" + node.value); // 打印当前节点的值
                f(node.next); // 递归调用函数，传入下一个节点作为参数
                //println("after:" + node.value); // 打印当前节点的值（在递归返回后）
            }
            //println("after:" + node.value); // 打印当前节点的值（在递归返回后）
        }
        //println("after:" + node.value); // 打印当前节点的值（在递归返回后）
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

现在开始添加null

• 调用 f 函数完后，继续判断。node = null ，所以在ifif判断里就已经完成满足条件了，就可以直接返回，退出该 f 函数。
• 因为已经退出了，所以后续就无需打印了。

 void f(Node node = 1) {
       /* if (node == null) {
            return;
        }*/
        println("before:" + node.value); // 打印当前节点的值
          void f(Node node = 2) {
                 /* if (node == null) {
            	    return;
                 }*/
            println("before:" + node.value); // 打印当前节点的值
                 void f(Node node = 3) {
              	  //if (node == null) {
                  	  return;
             	  // }
                println("before:" + node.value); // 打印当前节点的值
                     void f(Node node) {
                        if(node == null) {
                            return;
                        }
      		}
                //println("after:" + node.value); // 打印当前节点的值（在递归返回后）
            }
            //println("after:" + node.value); // 打印当前节点的值（在递归返回后）
        }
        //println("after:" + node.value); // 打印当前节点的值（在递归返回后）
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

通过对伪代码进行整合，最终代码如下，并会按我们所设置的1 -> 2 -> 3 -> null 进行输出：

// 1 -> 2 -> 3 -> null  f(1)

void f(Node node = 1) {
    println("before:" + node.value) // 1
    void f(Node node = 2) {
        println("before:" + node.value) // 2
        void f(Node node = 3) {
            println("before:" + node.value) // 3
            void f(Node node = null) {
                if(node == null) {
                    return;
                }
            }
            println("after:" + node.value) // 3
        }
        println("after:" + node.value) // 2
    }
    println("after:" + node.value) // 1
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

思路

1. 确定能否使用递归求解
2. 推导出递推关系，即父问题与子问题的关系，以及递归的结束条件

例如之前遍历链表的递推关系为
$$f(n)=\{\begin{array}{ll}停止& n=null\\ f(n.next)& n\ne null\end{array}$$

• 深入到最里层叫做递
• 从最里层出来叫做归
• 在递的过程中，外层函数内的局部变量（以及方法参数）并未消失，归的时候还可以用到

n是指的是从0开始：

public static void fangxiang(int n ,String str)
    {
        if(n == str.length())
        {
            return;
        }
        fangxiang(n + 1 ,str);
        System.out.println(str.charAt(n));
    }

    public static void main(String[] args) {
        fangxiang(0,"1234");
    }
1
2
3
4
5
6
7
8
9
10
11
12
13

2）单路递归 Single Recursion

E01. 阶乘

用递归方法求阶乘

• 阶乘的定义 $n!=1\cdot 2\cdot 3\cdots (n-2)\cdot (n-1)\cdot n$，其中 $n$ 为自然数，当然 $0!=1$

• 递推关系

$$f(n)=\{\begin{array}{ll}1& n=1\\ n\ast f(n-1)& n>1\end{array}$$

参考代码及解释如下：

​ 我们可以定义了一个名为f的静态方法，接受一个整数参数n，并返回n的阶乘。在方法内部，首先判断n是否等于1，如果是，则直接返回1，因为1的阶乘是1。否则，通过递归调用**f(n-1)来计算n-1的阶乘，并将结果乘以n**得到n的阶乘。

​ 在main方法中，调用了f(5)来计算5的阶乘，并将结果赋值给变量f。然后使用System.out.println语句输出结果，显示"5的阶乘为："加上计算得到的阶乘值。

public static int f(int n)
    {
        if(n == 1)
        {
            return 1;
        }
        return n * f(n-1);
    }

    public static void main(String[] args) {
        int f =f(5);
        System.out.println("5的阶乘为："+f);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13

或者你可以将主方法改变一下，使用Scanner 类 来将我们输入的值来计算阶乘，使得计算时可以更加灵活。

   public static int f(int n)
    {
        if(n == 1)
        {
            return 1;
        }
        return n * f(n-1);
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        System.out.println("请输入一个整数：");
        int n = scanner.nextInt();
        int f =f(n);
        System.out.println(n+"的阶乘为："+f);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

输出结果如下：

伪代码拆解演示

取 f 方法进行拆解，拆解伪码如下：

   public static int f(int n)
    {
        if(n == 1)
        {
            return 1;
        }
        return n * f(n-1);
    }
1
2
3
4
5
6
7
8

假设 n 初始值为 3：

• 传入int n = 3 后，不满足if的（n等于1）的判断，因此继续往下走
• 返回 3 * f（2）
• 接下来我们就要继续去计算f（2）

   public static int f(int n = 3)
    {
        /*if(n == 1)
        {
            return 1;
        }*/
        return n * f(3-1);
    }
1
2
3
4
5
6
7
8

此时来计算当 n 值为 2：

• 传入int n = 2 后，不满足if的（n等于1）的判断，因此继续往下走
• 返回 2 * f（1）
• 接下来我们就要继续去计算f（1）

   public static int f(int n = 3)
    {
        /*if(n == 1)
        {
            return 1;
        }*/
        return n * f( int f(int n = 2)
            {
                /*if(n == 1)
                {
                    return 1;
                }*/
                return n * f(2-1););
            }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

此时来计算当 n 值为 1：

• 传入int n = 1 后，满足if的（n等于1）的判断，因此直接返回1

   public static int f(int n = 3)
    {
        /*if(n == 1)
        {
            return 1;
        }*/
        return n * f( int f(int n = 2)
            {
                /*if(n == 1)
                {
                    return 1;
                }*/
                return n * f(int f(int n = 1)
                    {
                        if(n == 1)
                        {
                            return 1;
                        }
                        //return n * f(3-1);
                    }););
            }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

整合代码后，可以得到 3 的阶乘为 3 * 2 * 1 = 6：

f(int n = 3) { // 解决不了,递
    return 3 * f(int n = 2) { // 解决不了,继续递
        return 2 * f(int n = 1) {
            if (n == 1) { // 可以解决, 开始归
                return 1;
            }
        }
    }
}
1
2
3
4
5
6
7
8
9

E02. 反向打印字符串

用递归反向打印字符串，n 为字符在整个字符串 str 中的索引位置

• 递：n 从 0 开始，每次 n + 1，一直递到 n == str.length() - 1
• 归：从 n == str.length() 开始归，从归打印，自然是逆序的

递推关系
$$f(n)=\{\begin{array}{ll}停止& n=str.length()\\ f(n+1)& 0\le n\le str.length()-1\end{array}$$
代码及解释如下：

​ 这段代码定义了一个名为 f 的静态方法，它接受两个参数：一个整数 n 和一个字符串 str。方法的作用是从字符串的第 n 个位置开始，依次打印出每个字符，并在每次打印后调用自身来处理下一个字符的位置。

​ 在 main 方法中，我们调用了 f 方法，并传入初始值 0 和字符串 "abcde"。这将导致从索引为 0 的字符开始打印，即第一个字符 a。然后，递归调用 f 方法，将 n 的值增加 1，继续处理下一个字符。在递归返回后，再次打印当前字符 a。这样，会依次打印出字符串中的每个字符。

 public static void f(int n , String str)
    {
        if(n == str.length())
        {
            return;
        }
        System.out.println(str.charAt(n));
        f(n+1, str);
        System.out.println(str.charAt(n));
    }

    public static void main(String[] args) {
        f(0,"abcde");
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14

输出结果如下，前五个字符代表是正向打印，后面便是反向打印：

伪代码拆解演示

拆解伪码如下，假设字符串为 “abc”

void reversePrint(String str, int index = 0) {
    void reversePrint(String str, int index = 1) {
        void reversePrint(String str, int index = 2) {
            void reversePrint(String str, int index = 3) { 
                if (index == str.length()) {
                    return; // 开始归
                }
            }
            System.out.println(str.charAt(index)); // 打印 c
        }
        System.out.println(str.charAt(index)); // 打印 b
    }
    System.out.println(str.charAt(index)); // 打印 a
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

E03. 二分查找（单路递归）

具体的二分查找相关内容可以跳转到我另一篇博文。那边有更加详细的解法【点此跳转】

​ 这段代码定义了两个方法：f和find。f方法是递归函数，用于在数组 a 中进行二分查找，找到目标值 target(是要在数组里的数) 的索引。它接受四个参数：数组 a、目标值 target、起始索引 i和结束索引j`。

​ 在 f 方法中，首先判断起始索引 i是否大于结束索引j，如果是，则返回 -1，表示未找到目标值。然后计算中间索引 m，通过将 i 和 j 相加后右移一位得到。接下来，根据目标值与中间值的大小关系，递归调用 f 方法来缩小查找范围。如果目标值小于中间值，则在左半部分继续查找；如果中间值小于目标值，则在右半部分继续查找；如果相等，则找到了目标值，返回中间索引 m。

​ find 方法是一个包装器（wrapper）方法，用于调用 f 方法并传入初始的起始索引和结束索引。它接受两个参数：数组 a 和目标值 target，并返回目标值在数组中的索引。

​ 在 main 方法中，定义了一个有序整数数组 a，并调用 find 方法来查找目标值 4 在数组中的位置。在这个例子中，目标值 4 存在于数组中，所以输出结果为该值的索引，即 3。

// 定义一个递归函数f，用于在有序数组a中查找目标值target的索引
private static int f(int[] a, int target, int i, int j) {
    // 如果i大于j，说明子数组为空，返回-1表示未找到
    if (i > j) {
        return -1;
    }
    // 计算中间索引m
    int m = (i + j) >>> 1;
    // 如果目标值小于中间值，说明目标值在左半部分，递归查找左半部分
    if (target < a[m]) {
        return f(a, target, i, m - 1);
    // 如果目标值大于等于中间值，说明目标值在右半部分或者就是中间值，递归查找右半部分或者返回中间值索引
    } else if (a[m] < target) {
        return f(a, target, m + 1, j);
    } else {
        // 目标值等于中间值，返回中间值索引
        return m;
    }
}

// 定义一个公共静态方法find，用于调用递归函数f查找目标值target的索引
public static int find(int[] a, int target) {
    return f(a, target, 0, a.length - 1);
}

// 定义主函数
public static void main(String[] args) {
    // 定义一个有序数组a和目标值target
    int[] a = {1, 4, 6, 8, 12, 34};
    int index = find(a, 4);
    // 输出目标值对应的索引
    System.out.println("其对应的索引为：" + index);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

E04. 冒泡排序（单路递归）

• 将数组划分成两部分[0……j]i+1……a.length-1]
• 左边[0……j]是未排序部分
• 右边[i+1……a.length-1]是已排序部分
• 未排序区间内，相邻的两个元素比较，如果前一个大于后一个，则交换位置

起初最先是像这样前面四个没按顺序，后面两个按顺序排好的数组：

第一次冒泡排序我们可以知道前面的 4 大于 3 ，所以要把 4 和 3 进行对调。

第二次冒泡排序我们可以知道前面的 4 大于 2 ，所以要把 4 和 2 进行对调。

第三次冒泡排序我们可以知道前面的 4 大于 1 ，所以要把 4 和 1 进行对调。当我们想以4的角度继续冒泡排序的话，会发现4 < 5 ，无需对调，因此4已经到了合适的位置。

参考代码及解释如下：

​ 这段代码是一个冒泡排序算法的实现。它定义了一个bubble方法用于对数组进行冒泡排序，一个sort方法用于调用bubble方法对整个数组进行排序，以及一个main方法作为程序的入口。

​ 在bubble方法中，通过比较相邻的元素并交换位置，将较大的元素逐渐"冒泡"到数组的末尾。如果当前元素的下标为0，则直接返回，因为已经没有需要比较的元素了。

​ 在sort方法中，调用bubble方法对整个数组进行排序。参数a.length-1表示从数组的最后一个元素开始进行比较和交换。

​ 在main方法中，创建一个整数数组a并初始化为{4, 3, 2, 1, 6, 5}。然后调用sort方法对该数组进行排序。最后，使用Arrays.toString(a)将排序后的数组转换为字符串并打印输出。

// 定义一个私有静态方法bubble，用于对整型数组a进行冒泡排序
private static void bubble(int[] a, int j) {
    // 循环遍历数组a，从第一个元素到第j个元素
    for (int i = 0; i < j; i++) {
        // 如果当前元素大于下一个元素
        if (a[i] > a[i + 1]) {
            // 交换当前元素和下一个元素的值
            int t = a[i];
            a[i] = a[i + 1];
            a[i + 1] = t;
        }
    }
}

// 定义一个公共静态方法sort，用于调用bubble方法对整型数组a进行排序
public static void sort(int[] a) {
    // 调用bubble方法对数组a进行排序，从最后一个元素开始比较
    bubble(a, a.length - 1);
}

// 定义主函数
public static void main(String[] args) {
    // 创建一个整型数组a并初始化为{4, 3, 2, 1, 6, 5}
    int[] a = {4, 3, 2, 1, 6, 5};
    // 调用sort方法对数组a进行排序
    sort(a);
    // 输出排序后的数组a
    System.out.println(Arrays.toString(a));
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

输出结果如下：

当然，如果你想从头到尾冒泡完，就可以修改一些代码：

• ​ 它首先检查数组的长度，如果长度为0，则直接返回。
• ​ 然后，它遍历数组，比较相邻的两个元素，如果前一个元素大于后一个元素，就交换它们的位置。
• ​ 最后，它调用自己，将数组的长度减1，继续进行排序。
• ​ 这个过程会一直重复，直到数组的长度为0为止。

private static void bubble(int[] a ,int j)
    {
        if(j == 0)
        {
            return;
        }
        for(int i = 0; i < j; i++)
        {
            if(a[i] > a[i+1])
            {
                int t = a[i];
                a[i] = a[i+1];
                a[i+1] = t;
            }
        }
        bubble(a, j-1);
    }

    public static void sort(int[] a)
    {
        bubble(a,a.length-1);
    }

    public static void main(String[] args) {
        int[] a = {4,3,2,1,6,5};
        sort(a);
        System.out.println(Arrays.toString(a));
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

输出结果如下：

而对于上面冒泡排序中的 bubble(a, j-1); 是每次排序都要从第0个元素查找到 j-1 长度的元素，一旦后面都形成了有序列，这样的从头到尾查找就会做了很多的无用功，

因此我们新增一个变量 x ，给它以下设定：

• 当 i 与 i + 1 进行对调，就把 i 原先所指的节点值赋给 x
• 如果 i 与 i + 1 未进行对调 ， x 就保持原来的值

1、如图解，从第0个元素开始判断，由于未进行对调，因此x = i = 0

2、因为 i 所对应的值大于 i+1 的值，因此两个元素进行调换，同时 x 等于原来i所对应的下标索引。

3、同理，一直向下去调换。

4、当我们来到 i < i+1 的步骤后，就能发现 x 其所对应的下标索引的右边均是有序数组了，剩下我们只需要在 x 的左边进行排序，不用在做多余的无用功。

参考代码如下：

private static void bubble(int[] a, int j) {
    // 定义一个变量x，用于记录最后一次交换的位置
    int x = 0;
    if (j == 0) {
        return;
    }
    for (int i = 0; i < j; i++) {
        if (a[i] > a[i + 1]) {
            int t = a[i];
            a[i] = a[i + 1];
            a[i + 1] = t;
            x = i;
        }
    }
    // 递归调用bubble方法，将最后一次交换的位置作为参数传入
    bubble(a, x);
}

public static void sort(int[] a) {
    bubble(a, a.length - 1);
}

public static void main(String[] args) {
    int[] a = {4, 3, 1, 2, 6, 5};
    sort(a);
    System.out.println(Arrays.toString(a));
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

输出结果如下：

E05. 插入排序（单路递归）

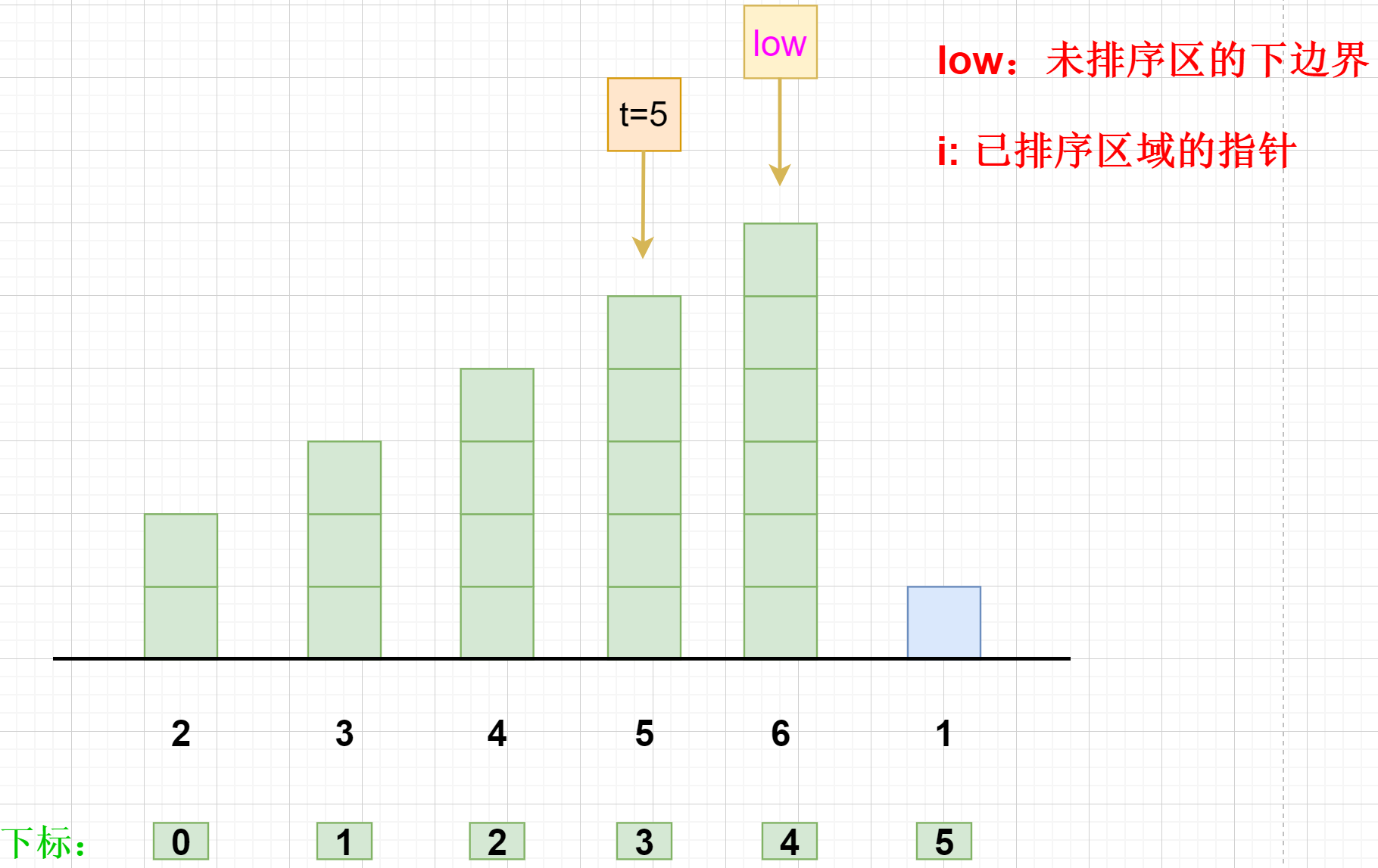
​ 下面是我们示例的一个需要排序的数组，绿色区域是已经排好序的了，而蓝色区域是还需要排序的。

​ 接收的整个数组叫做a ，未排序区的下边界称之为 low ，而 i 为已经排好序的区域的指针。

​ 那么现在开始插入排序了。首先 low 指针会从后往前遍历，如果当前元素小于前一个元素，则将前一个元素向后移动一位，直到找到合适的位置插入当前元素。如 5 < 6 ， 则将 6 往后面移动一位，空出一个位置。

【从后往前找，只要能找到一个比t小的就能插入了，因为前面已经是排好顺序的】

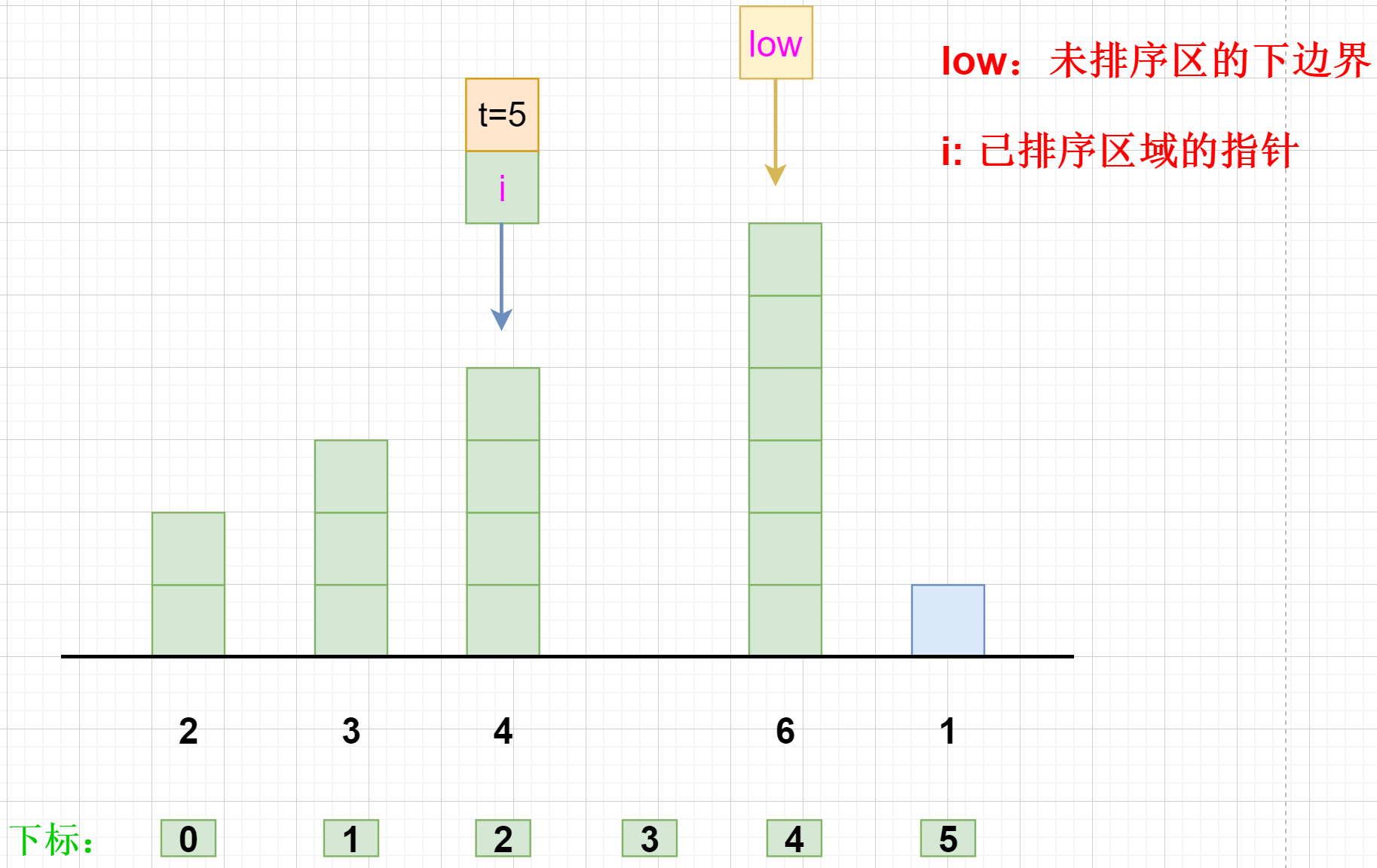
​ 再进行下一次判断，发现 5 比 4 大 ，就不用再往下走了，就可以把5插在右边的空位上了， 此时 2 - 6 均是排好序的。

​ 所以我们可以先设置一个私有静态方法，用于实现插入排序的递归过程。它接受一个整数数组和一个下标作为参数。如果下标等于数组长度，那么递归结束；否则，取出待插入的元素，并在已排序的子数组中找到合适的位置插入，然后递归处理下一个元素。

 private static void insertion(int[] a, int low) {
        if (low == a.length) {
            return;
        }
        int t = a[low]; // 取出待插入的元素
        int i = low - 1;
        while (i >= 0 && a[i] > t) { // 没有找到插入位置则不断循环
            a[i + 1] = a[i]; // 空出位置（右边赋给左边，从而腾出i+1 的位置）
            i--; // 继续从右向左去寻找
        }
        a[i + 1] = t;
        insertion(a, low + 1); // 递归处理下一个元素
    }
1
2
3
4
5
6
7
8
9
10
11
12
13

​ 以此之外，我们需要再写一个公共类，用来对外提供的排序接口，用来调用上述的插入排序递归方法，传入数组和起始下标1的时候会更加方便。

 public static void sort(int[] a) {
        insertion(a, 1);
    }
1
2
3

​ 最后写一个主类，主要用于让我们测试一下这段代码是否能正常运行。首先创建一个扫描器对象用于接收用户输入，然后提示用户输入数组的长度和元素，最后调用排序方法进行排序，并输出排序后的数组。

下面是完整的代码：

import java.util.Arrays;
import java.util.Scanner;

public class 插入排序 {
    // 插入排序的递归实现
    private static void insertion(int[] a, int low) {
        if (low == a.length) {
            return;
        }

        int t = a[low]; // 取出待插入的元素
        int i = low - 1;
        while (i >= 0 && a[i] > t) { // 没有找到插入位置则不断循环
            a[i + 1] = a[i]; // 空出位置
            i--; // 继续从右向左去寻找
        }
        a[i + 1] = t;
        insertion(a, low + 1); // 递归处理下一个元素
    }

    // 对外提供的排序接口
    public static void sort(int[] a) {
        insertion(a, 1);
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        System.out.println("请输入数组长度：");
        int n = scanner.nextInt();
        int[] arr = new int[n];
        System.out.println("请输入数组元素：");
        for (int i = 0; i < n; i++) {
            arr[i] = scanner.nextInt();
        }
        sort(arr); // 调用排序方法
        System.out.println("排序后的数组为：");
        System.out.println(Arrays.toString(arr)); // 输出排序后的数组
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

输出结果如下：

注意点

1、当我们从右向左查找的时候，发现 i 比 待插入值 还小，那 i + 1 的位置不就是待插入的位置了嘛？那就没有必要在把i + 1 赋给 t 了。（也就是说low是被插入区域内大的，就还是在原来的位置，就不用动位置了）

可以把那段 a[i + 1] = t; 修改成：

 if(i + 1 != low)
        {
            a[i+1] = t;
        }
1
2
3
4

这样一来，当i + 1 等于low后，就不必要再赋值了。