-
医学案例|线性回归
一、案例介绍
某医师预研究糖尿病患者的总胆固醇和甘油三酯对空腹血糖的影响,某研究者调查40名糖尿病患者的总胆固醇、甘油三酯和空腹血糖的测量值如下,试根据上述研究问题作统计分析。
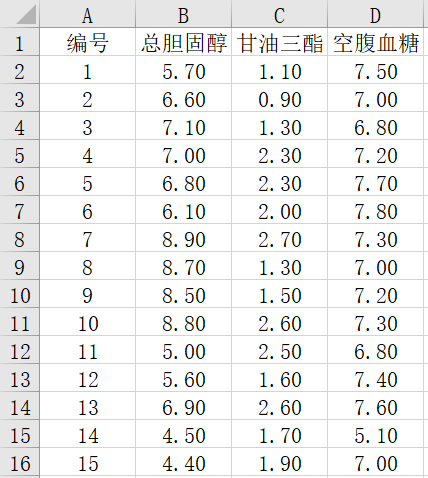
二、问题分析
本案例想要研究一些变量(总胆固醇和甘油三酯)对另一变量(空腹血糖)的影响,可以使用多元线性回归分析进行研究。多元线性回归分析比较重要的假设有以下5个:
假设1:线性——因变量与自变量之间存在线性关系
假设2:独立性——各观测值之间相互独立,即残差之间不存在自相关。
假设3:正态性——残差接近正态分布。
假设4:方差齐——残差的方差齐。
假设5:多重共线性——自变量间不存在多重共线性。
如果违反了这些假设中的一个或多个,那么可能导致线性回归分析结果不可靠。因此我们需要对假设1-5使用软件进行检验。
三、前提假设检验
(1)检验假设1:线性
多元线性回归分析要求因变量Y与自变量X之间存在线性关系。针对连续型自变量,可以通过绘制自变量与因变量的散点图,直观判断是否存在线性关系。而对于分类自变量(如学历),可以忽略与因变量之间的线性关系。
使用SPSSAU分别绘制Y空腹血糖和X1总胆固醇、X2甘油三酯的散点图,在【可视化】模块选择【散点图】,将数据拖拽到右侧相应分析框中,点击开始分析,操作如下图:
SPSSAU输出散点图如下:
①总胆固醇和空腹血糖散点图
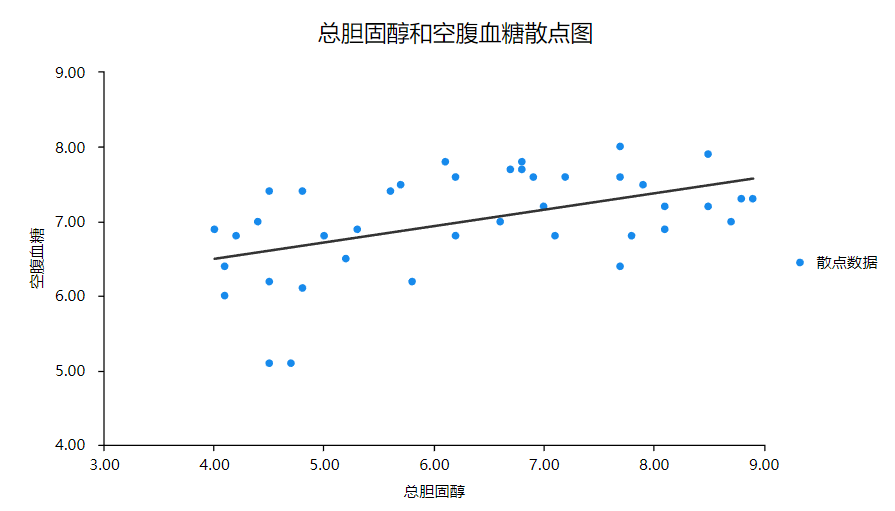
以“空腹血糖”作Y轴,“总胆固醇”作X轴绘制散点图,可以看出,空腹血糖与总胆固醇之间存在线性关系。
②甘油三酯和空腹血糖散点图
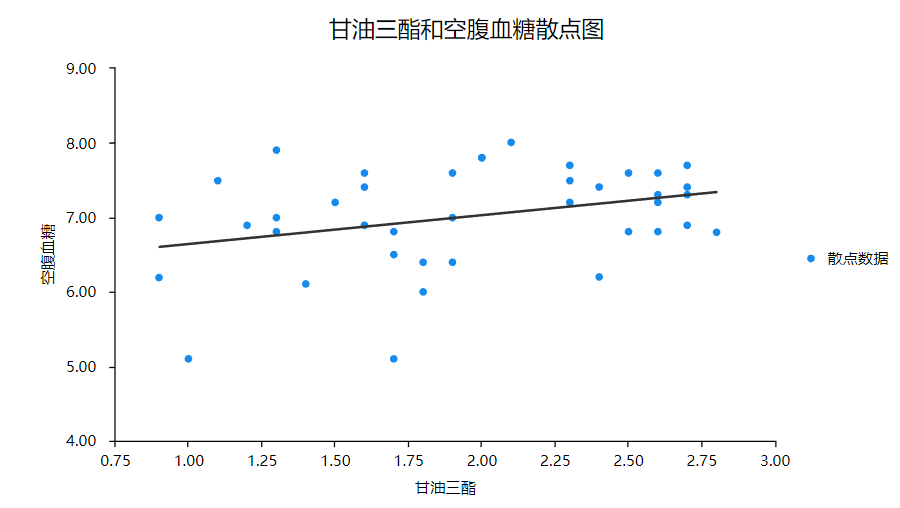
同理查看甘油三酯与空腹血糖绘制的散点图,二者之间存在近似线性关系。
综上,可以认为本案例数据满足假设1:,即因变量与自变量之间存在线性关系。
(2)检验假设2:独立性
线性回归分析假设各个观测值之间是相互独立的,即残差之间不存在自相关。可以使用Durbin-Watson检验残差是否存在自相关。
SPSSAU线性回归分析结果会输出D-W检验结果,如下图:
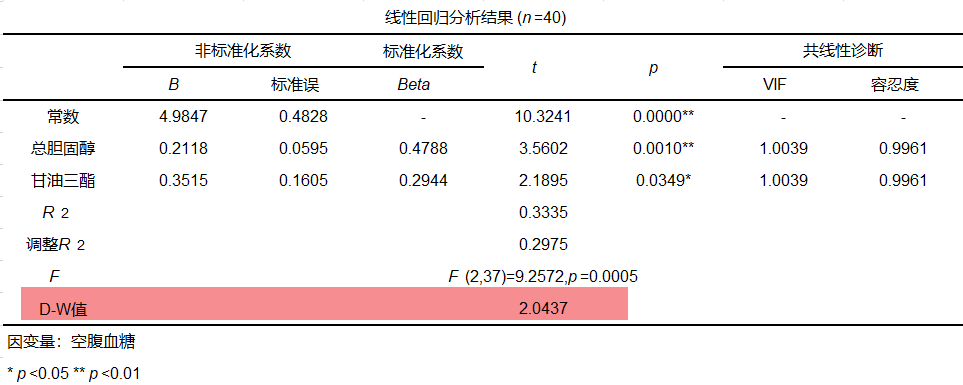
一般来说,D-W检验其值在0到4之间。如果D-W检验值接近0,说明存在正自相关,如果接近4,说明存在负自相关。一般认为,如果D-W检验值在1.5到2.5之间,就说明不存在自相关问题。从上表可知,本案例D-W值为2.0437,因此认为不存在自相关,所以数据满足假设2,即各观测值之间相关独立。
(3)检验假设3:正态性
线性回归假设中的正态性是指残差(即随机扰动项)近似服从正态分布。首先得到残差值,在使用SPSSAU进行线性回归时,勾选“保存残差和预测值”,操作如下图:
正态分布检验的方法有很多种,例如直方图、P-P图/Q-Q图、统计检验等。本案例使用P-P图进行正态性检验,得到残差P-P图如下:
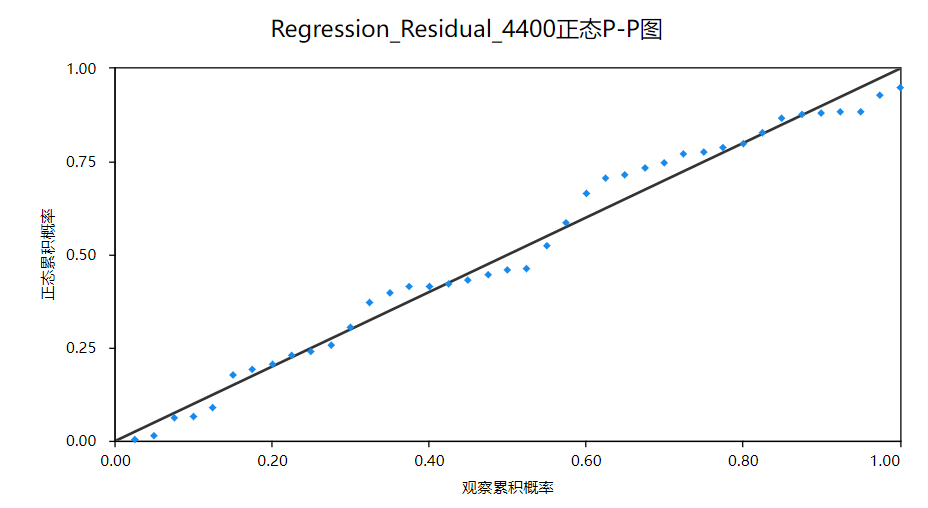
P-P图近似呈现为一条对角直线,说明数据接近正态分布。从上图可以看到,残差的P-P图近似为一条对角直线,故认为残差基本满足正态分布,满足假设3。
(4)检验假设4:方差齐
多元线性回归方差齐指的是残差项在不同自变量取值下具有相同的方差,即各组残差具有相同的离散程度。可以通过绘制标准化预测值与标准化残差的散点图来检验多元线性回归的方差齐性。以标准化预测值为横坐标,以标准化残差为纵坐标,绘制散点图。
①数据标准化处理
首先将保存的残差值和预测值进行标准化处理,在SPSSAU【数据处理】模块,选择【生成变量】,选中残差值和预测值,在“量纲处理”选择标准化处理,点击“确认处理”,操作如下图:

②散点图绘制
以标准化预测值为X轴,以标准化残差为Y轴,绘制散点图,得到散点图如下:
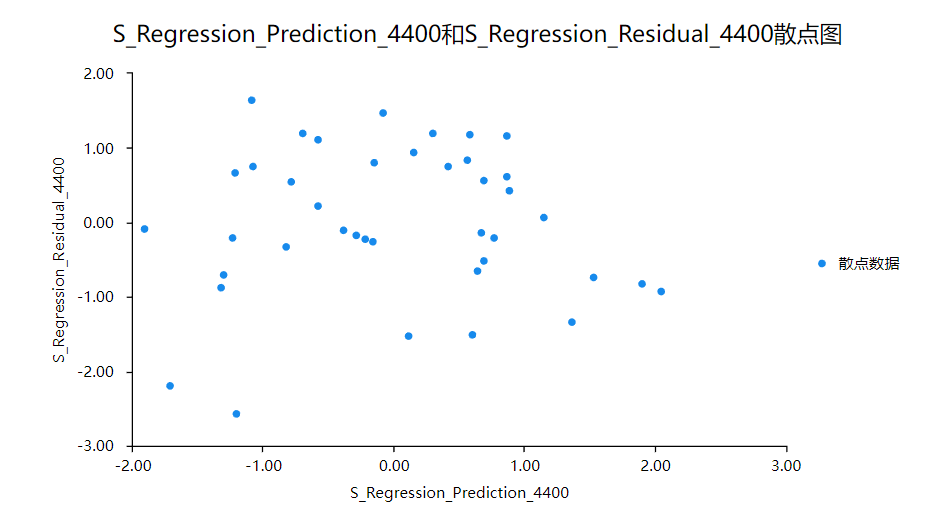
如果方差齐性假设成立,则散点图中的点应该大致均匀分布在坐标系中,散点的分布情况不会因为标准化预测值的变化而改变。从上图可以看出,散点基本均匀分布在坐标系中,无明显趋势,所以可以认为满足假设4,即残差近似满足方差齐性。
(5)检验假设5:多重共线性
自变量之间不存在多重共线性,如果存在多重共线性,那么自变量之间的线性关系会导致回归系数的估计变得不稳定,增加标准误差,从而影响预测的准确性。同时,多重共线性还会导致t检验和P值失去意义,无法准确判断自变量对因变量的影响。在多元线性回归分析中,我们通常使用方差膨胀因子(VIF值)来检测多重共线性。
SPSSAU线性回归分析结果输出共线性诊断结果如下:
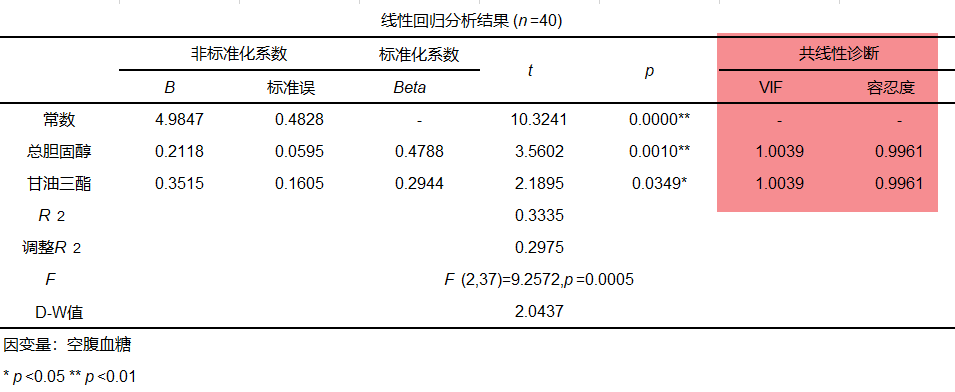
SPSSAU同时输出VIF值和容忍度值(容忍度=1/VIF,二者选其一即可,通常描述VIF值)。一般认为,当VIF值大于5时(或容忍度小于0.2),存在严重的多重共线性问题。分析上表知,VIF值均小于5,所以认为本案例自变量之间不存在多重共线性问题,满足假设5。
如果存在共线性问题,可以通过移除共线性变量、使用逐步回归、岭回归或者增加样本量等方式进行处理。
综上所述,本案例数据满足使用多元线性回归分析的假设,可以进行分析。
四、线性回归分析
本案例线性回归分析结果如下:

对于多元线性回归模型的检验可以分为两部分:①多个自变量与因变量这个整体的显著性检验(F检验);②每个自变量对因变量影响的显著性检验(t检验),二者检验目的不同。
(1)模型检验
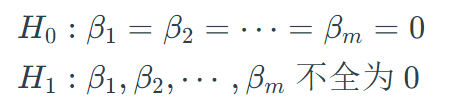
H 0 : β 1 = β 2 = ⋯ = β m = 0 H 1 : β 1 , β 2 , ⋯ , β m 不全为 0 检验统计量
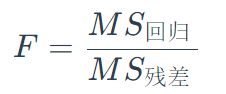
F=\frac{MS_\text{回归 }}{ M S _\text{残差 }}
当H0为真时,统计量F服从自由度为m和n-m-1的F分布,其中,n为样本量,m为回归模型中的自变量个数,加入自变量回归系数全为0,则Y与各个自变量没有任何关系,这就失去了建立回归方程的意义,故当检验结果为拒绝H0时,称该回归模型是有统计学意义的。
SPSSAU多元线性回归分析F检验输出结果如下:
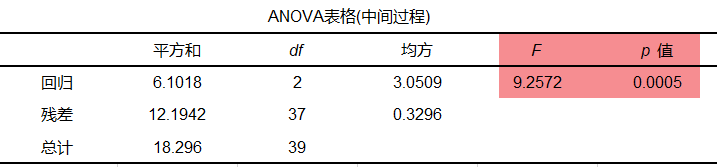
从上表回归模型方程分析结果可知,F=9.2572,p=0.0005<0.05,所以拒绝原假设H0,即回归模型有统计学意义。
(2)单个回归系数检验
回归系数显著性检验是指每个自变量对因变量影响的显著性检验,使用t检验进行。SPSSAU输出每个自变量对因变量影响的t检验结果如下:

分析上表可知,总胆固醇与甘油三酯对应t检验的p值均小于0.05,说明两变量均对空腹血糖具有显著影响。
(3)影响大小比较
自变量对因变量影响大小的比较是通过标准化回归系数进行比较的。标准化回归系数的绝对值越大,说明该自变量对因变量的影响越大。
标准化回归系数,是对自变量和因变量同时进行标准化处理后所得到的回归系数,数据经过标准化处理后消除了量纲、数量级等差异的影响,是的不同变量之间具有可比性,因此使用标准化回归系数比较不同自变量对因变量的影响大小。
分析结果可知,总胆固醇和甘油三酯的标准化回归系数分别为0.4788和0.2944,说明二者均对空腹血糖有显著正态性影响,且相对来讲总胆固醇的影响更大一些。
(4)模型公式
从分析结果可以看出,模型公式为:空腹血糖=4.985 + 0.212*总胆固醇 + 0.351*甘油三酯,模型R方值为0.334,意味着总胆固醇、甘油三酯可以解释空腹血糖的33.4%变化原因。
特别提示:构建回归模型使用非标准化回归系数,它是方程中不同自变量对应的原始回归系数,反映了在其他自变量不变的情况下,该自变量每变化一个单位对因变量作用的大小。通过非标准化回归系数构建的回归方程,才可以对因变量进行预测。
更多分析结果可登录SPSSAU查看,在此不再进行赘述。
五、结论
本案例使用多元线性回归分析研究总胆固醇和甘油三酯对空腹血糖的影响,研究发现,总胆固醇和甘油三酯均会对空腹血糖产生显著正向影响,其中总胆固醇的影响更大一点。
六、知识小贴士
(1)R方值多少合适?
R平方值表示模型拟合能力的大小,比如0.3表示自变量X对于因变量Y有30%的解释能力。这个值介于0~1之间,越大越好。但实际研究中并没有固定的标准,有的专业0.1甚至0.05这样都可以,但有的专业却常常出现0.8以上。一般情况下只需要报告此值即可,不用过多关注其大小,原因在于多数时候我们更在乎X对于Y是否有影响关系即可。
(2)回归系数非常非常小或者非常非常大?
如果说数据的单位很大,不论是自变量X还是因变量Y;此种数据会导致结果里面的回归系数出现非常非常小,也或者非常非常大。此种情况是正常现象,但一般需要对数据进行统一取对数处理,以减少单位问题带来的‘特别大或特别小的回归系数’问题。
-
相关阅读:
【数据结构】线性结构——数组、链表、栈和队列
Ajax零基础入门 Ajax零基础入门第三天 3.3 封装自己的Ajax函数 && 3.4 XMLHttpRequest Level2的新特性
内存管理篇——物理内存的管理
【BOOST C++ 18 数字处理】(4)Boost.Random
深入浅出 JavaScript 中的 this
JAVA 学习路线 学习大纲(java 进阶路线)
集合基础(ArrayList)
Android为TV端助力 完全解析模拟遥控器按键
lambda表达式
C#操作GridView控件绑定数据实例详解
- 原文地址:https://blog.csdn.net/m0_37228052/article/details/132587437