【蓝桥】数树数

一、题目

1、题目描述

给定一个层数为 $n$ 的满二叉树，每个点编号规则如下：

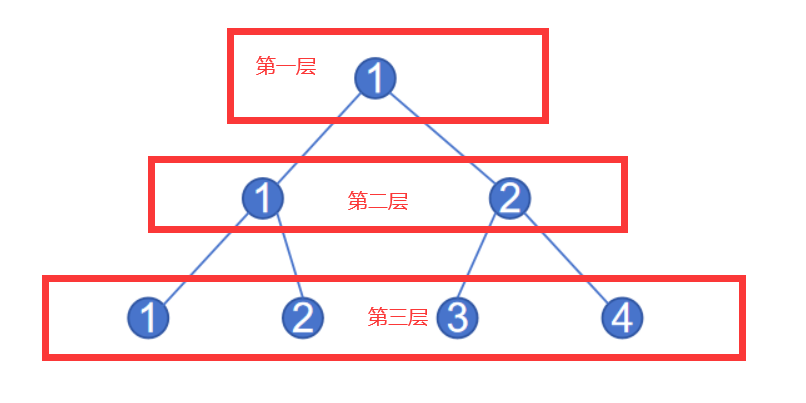
具体来说，二叉树从上往下数第 $p$ 层，从左往右编号分别为：1,2,3,4，…, 2^p-1。

给你一条从根节点开始的路径，想知道到达的节点编号是多少？

例如，路径是 $right-left$，那么到达的节点是 $1-2-3$，最后到了三号点，如下图所示：

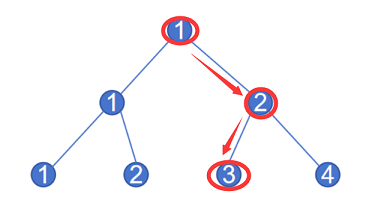
输入格式：

第一行输入两个整数 $n$，$q$，$n$ 表示完全二叉树的层数，$q$ 代表询问的路径数量。

接下来 $q$ 行，每行一个字符串 $S$，$S$ 只包含字符 { 'L','R'}，L 代表向左，R 代表向右。

输出格式：
输出 $q$ 行，每行输出一个整数，代表最后到达节点的编号。

样例输入

3 6
R
L
LL
LR
RL
RR
1
2
3
4
5
6
7

样例输出：

2
1
1
2
3
4
1
2
3
4
5
6

说明：
$2\le n\le 20,1\le q\le 10^3,1\le |S|<n$。

完全二叉树： 一个二叉树，如果每层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为 $k$，且节点总数为 $2^{k-1}$，则它就是满二叉树。

2、基础框架

#include 
using namespace std;

int main()
{   
	// 请在此输入您的代码
	return 0;
}
1
2
3
4
5
6
7
8

3、原题链接

数树数

二、解题报告

1、思路分析

解法1：暴力解

建立起一棵 $n$ 个节点的完全二叉树，然后标号，暴力走路径。

时间复杂度 $O(2^n+\sum |S|)$

解法2：计算

利用满二叉树的性质，第 $i$ 层的节点数量是 $2^{i-1}$ 个。

在一条路径上，实际上与 $n$ 并无关系，只与最后到达的层数有关，所以只与路径的长度有关，维护当前点的编号 $id$ ，初始值为 $1$ ，如果路径长度是 $p$ ，那么最后到达的层数就是 $p$ ，当前所在的层数是 $q$ ，那么当前节点的子树的叶节点总数就是 $2^{p-q}$ 。

如果向左，则到达下一层，并且 $id$ 不变；如果向右，就是跨越了 $2^{p-q-1}$ 个节点（当前节点的左树的节点全部排除）， $id$ 加上 $2^{p-q-1}$。

时间复杂度： $O(\sum |S|)$ 。

2、代码详解

• 暴力解

#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;
const int N = 2e6 + 100;
const int MOD = 998244353;

int L[N], R[N], val[N];
int depVal[N];
int op = 1;

void build(int u, int dpt) {
    val[u] = ++depVal[dpt];
    if (dpt == 20) {
        return;
    }
    L[u] = ++op;
    build(L[u], dpt + 1);
    R[u] = ++op;
    build(R[u], dpt + 1);
}
char s[40];

void dfs(int u, char *c) {
    if (*c == '\0') {
        cout << val[u] << '\n';
        return;
    }
    if (*c == 'L') {
        dfs(L[u], c + 1);
    } else {
        dfs(R[u], c + 1);
    }
}

void sol() {
    build(1, 1);
    int n, q;
    cin >> n >> q;
    while (q--) {
        cin >> s;
        dfs(1, s);
    }
}

int main() {
    // ios::sync_with_stdio(0);
    // cin.tie(0);
    // cout.tie(0);
    int T = 1;
    // cin >> T;
    while (T--) {
        sol();
    }
    exit(0);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

• 计算法

#include 
using namespace std;

int main()
{   
    int n;
    int q;
    cin >> n;
    cin >> q;

    string s;
    
    while (q--) {
        cin >> s;
        int len = s.size();
        int ans = 1;
        for (int i = 0; i < len; i++) {
            if (s[i] == 'R') {
                ans += (1 << (len - i - 1)); //左树上的节点跳过
            }   
        }
        cout << ans << endl;
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25