堆专题4 堆排序

题目：

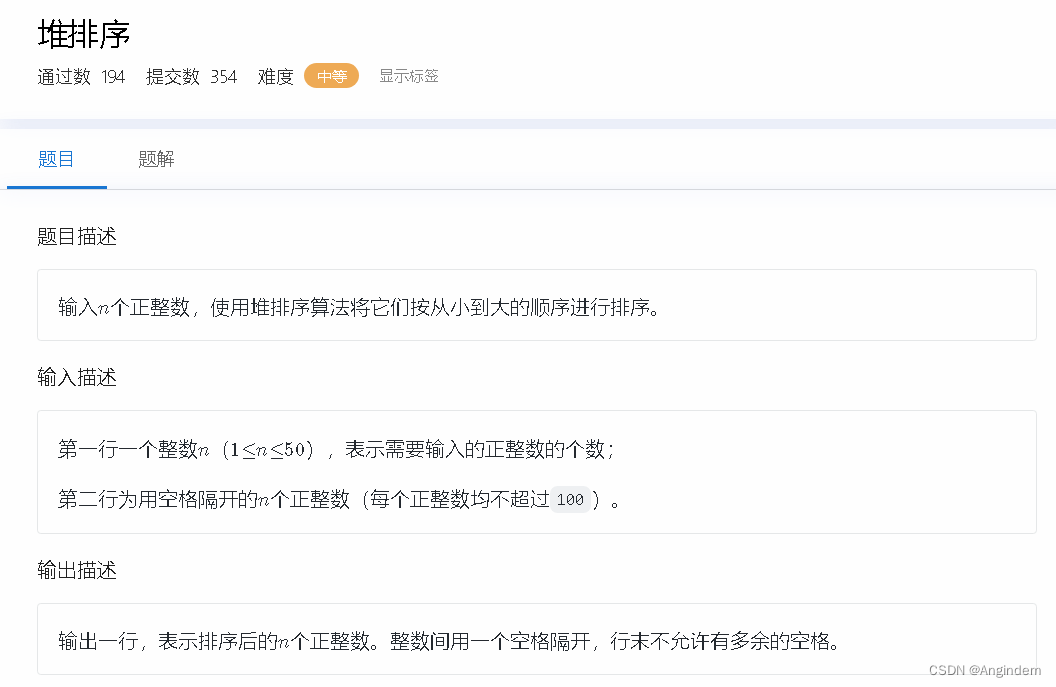
样例：

5
2 8 5 1 3

思路：

        由题意，堆的排序，就是结合向下或向上调整的方式，调整堆顺序，全部的各个部分都变为 顶堆形式。不同的是，由于我们是顶堆原理，我们取的是顶部，所以使用向下调整方式更为方便些，

此时我们将最小的堆顶放置在堆数组末尾，

即我们要倒着枚举 从 n 开始 for(int i = n;i;--i) 将 堆顶数值  放置在堆的后面swap(1,i)然后 调整我们没取得的 downAdjust(1,i - 1)。

最后根据 根部向下的调整，我们会获得一个递减或者递增的序列，

如果是小顶堆，根据向下调整，堆的排序，我们会获得一个递减序列，因为 downAdjust(1,i - 1) 使得 左右孩子的大小比较的调整，得出层序数组的 heap 是个递减序列。

如果是大顶堆，堆排序后是 递增序列。

代码详解如下：

#include 
#include 
#include 
#include 
#include 
#define endl '\n'
#define x first
#define y second
#define mk make_pair
#define int long long
#define NO puts("NO")
#define YES puts("YES")
#define umap unordered_map
#define INF 0x3f3f3f3f3f3f3f3f
#define All(x) (x).begin(),(x).end()
#pragma GCC optimize(3,"Ofast","inline")
#define ___G std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
 
using namespace std;
const int N = 2e6 + 10;
using PII = pair<int,int>;
 
int n;
umap<int,int>heap;
 
// 向下调整 大顶堆
inline void downAdjust(int low,int high)
{
	int i = low,j = i << 1;
	while(j <= high)
	{
		if(j + 1 <= high && heap[j + 1] > heap[j]) ++j;
		if(heap[j] > heap[i])
		{
			swap(heap[j] , heap[i]);
			i = j;
			j = i << 1;
		}else return ;
	}
}
 
inline void sortHeap()
{
	// 调整创建 大顶堆
	for(int i = n >> 1;i;--i) downAdjust(i,n);
	
	// 创建小顶堆后，我们每次根据大顶堆的顶部最大原理
	// 调整到 堆后面，最后 向下调整 获得递增序列
	for(int i = n;i;--i)
	{
		swap(heap[1],heap[i]);	// 顶堆元素放在 堆后面，交换 顶堆 和 尾堆
		downAdjust(1,i - 1);	// 向下调整我们 没取到的 堆, 尾堆是我们取到的，所以不能调整 ,所以是 i - 1
	}
}
 
inline void solve()
{
	cin >> n;
	// 插入对数组中
	for(int i = 1;i <= n;++i) cin >> heap[i];
	
	sortHeap();
	
	for(int i = 1;i <= n;++i)
	{
		if(i > 1) cout << ' ';
		cout << heap[i];
	}
}
signed main()
{
//	freopen("a.txt", "r", stdin);
	___G;
	int _t = 1;
//	cin >> _t;
	while (_t--)
	{
		solve();
	}
 
	return 0;
}

最后提交：