感知机模型

前言

感知机是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1 和 -1 二值。感知机对应于输入空间中（特征空间）将实例划分为正负两类的分离超平面，也就是所谓的感知机模型就是将输入空间中的点建立一个平面来将它们分离开来，属于判别模型。感知机学习旨在求出将训练数据进行线性划分的分离超平面，但根据我们的常识能知道一般可以分离的超平面是能求出好多个的，但是它的分类能力各有好坏，有的泛化能力差一些，有的泛化能力更好。为此，导入基于误分类的损失函数，利用梯度下降法对损失函数进行极小化，求得根据梯度下降来说的最好的感知机模型。感知机学习算法具有简单而易于实现的优点，分为原始形式和对偶形式。感知机预测是用学习得到的感知机模型对新的输入实例进行分类，也就是先用训练数据求得了较好的感知机模型，再用其来进行分类。感知机是神经网络与支持向量机的基础。

2.1 感知机模型

假设输入空间是   ,输出空间是  。输入  表示实例的特征向量 ，对应于输出空间（特征空间）的点；输出 表示实例的类别。由输入空间到输出空间的如下函数：

称为感知机。其中，w 和 b 为感知机模型参数，叫做权值或权值向量，叫做偏置，w.x表示w 和 x的内积。sign 是符号函数，即

 通过这个线性分类模型就将输入的所有实例分成了两类，感知机模型的假设空间是定义在特征空间中的所有线性分类模型或线性分类器，即函数集合。

感知机有如下几何解释：线性方程

w.x + b = 0

 对应于特征空间中的一个超平面 S ，其中 W 是超平面的法向量，b是超平面的截距 。这个超平面将特征空间划分为两个部分。位于两部分的点（特征向量）分别被分为正负两类。因此，超平面 S 称为分离超平面。

 感知机学习，由训练数据集（实例的特征向量及类别）

其中， ,,求得感知机模型，即求得模型参数w,b。感知机预测，通过学习得到的感知机模型，对于新的实例给出其对应的输出类别。

感知机模型，就和其它那些许多分类模型的实现思想一致，因为它本身也是SVM和神经网络的基础，先用一部分数据训练和拟合等求出模型所需要的参数，然后再用于新数据的预测和验证。 

2.2 感知机学习策略

2.2.1 数据集的线性可分性 

给定数据集之后首先要证明数据集是线性可分的，如果存在某个超平面 S  

w.x + b =0

能够将数据集的正实例点和负实例点完全正确的划分到超平面的两侧，即对所有 y = +1 的实例 i , 有  ,对所有 y = -1 的实例 i ,有  ，则成数据集T 为线性可分数据集，否则不能满足条件的话称为线性不可分数据集。在超平面的两侧代入值后分别呈现不同的结果，对于所有的值都能划分完成则表明是线性可分的。

2.2.2 感知机学习策略

 加入上一步已经证明给定的数据集是线性可分的，感知机学习的目标是求得一个能将训练集正实例点和负实例点完全正确分开的分离超平面。为了找出这样一个分离超平面，即确定感知机模型参数 w和 b ,需要确定一个学习策略，也算是评价标准，如何计算出来的超平面才是最好的超平面，这里我们选择定义经验损失函数并将损失函数极小化求出最佳超平面。

损失函数的一个自然选择是误分类点的总数，但是通过选择误分类点的总数作为损失函数，它不是参数 w 和 b 的连续可导函数，不容易进行优化。损失函数的另一个选择是误分类点到超平面S的总距离，这是感知机采用的，这种情况下容易求得模型的参数 w 和 b 。

为此，首先写出输入空间 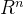 中任意一点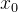到超平面S的距离

这里，||w||  是 w 的 L2 范数。

计算点到超平面和点到直线的距离如上所示.

对于误分类的数据来说，

因为正常情况下其 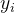  和其对应的  符号是相同的，所以在误分类情况下出现如上图所示情况。求得误分类点后，再计算所有误分类点到超平面S的距离之和，

在我们当前背景下是否考虑都对最后的模型中 w 和 b 的参数求解不构成影响，所以由此我们便可以得到感知机学习的损失函数。

 

2.3 感知机学习算法 

2.3.1 感知机学习算法的原始形式 

 此时确定一个点为误分类点之后就要开始对其更新，那如何对这个点进行更新呢，更新的原则就是其初始值加减它的学习率与其梯度的乘积。

 

根据对以上训练数据集的求解我们也可以看出，迭代过程是基于单独的一个点进行，并不是基于全体一块进行的，所以由此我们也可以得出每次选取的点的顺序不同，得出的答案的结果不同。

2.3.2 算法的收敛性 

前面我们对于已知的训练数据经过有限次计算得到了一个将训练数据集完全正确划分的分离超平面及感知机模型 ，但是对于未知数量的数据集我们如何才能证明可以在有限次计算内计算出分离超平面呢。

 2.3.3 感知机学习算法的对偶形式

感知机学习算法共有两种形式，一种形式是原始形式，一种形式是对偶形式，

 对偶形式的基本思想就是更换了输入参数的形式，改成了线性组合的形式。

 

格拉姆矩阵的计算如上所示。