量化初探: 对称量化以及非对称量化

1. 量化的定义以及好处

量化（Quantization）是指将高精度浮点数表示为低精度整数的过程，从而提高神经网络的效率和性能。在能够接受一定的精度损失的情况下，可以有以下的好处:

1. 减小内存占用

   • 模型大小减少：通过量化，我们可以将32位浮点数转换为较低位宽的数（例如8位整数）。这可以显著减少模型的大小，使其更容易在内存受限的设备上部署。
   • 减少带宽需求：模型大小的减少也意味着在下载或传输模型时需要的带宽减少。

2. 加速计算

   • 特定硬件加速：很多硬件（例如Jetson）对低位宽的操作更有优势，因此量化模型可以更好地利用这些硬件特性。
   • 并行化：低位运算可以允许更高的并行度，从而进一步加速计算。

3. 减小功耗和延迟

   • 减少计算复杂性：较低位宽的运算通常需要较少的计算资源，这意味着功耗可以降低。
   • 实时应用：在需要低延迟的场景（如自动驾驶或增强现实应用）中，量化可以帮助模型更快地做出预测。

4. 部署灵活性：由于量化模型更小、更快，它们可以更容易地部署在各种设备上，包括但不限于智能手机、IoT设备和边缘计算设备。

5. 提高能效比：在很多场景下，能效比（性能与功耗的比值）是一个关键指标。通过减少内存和计算需求，量化可以显著提高神经网络的能效比。

6. 降低部署成本：使用小型、低功耗的硬件部署量化模型可以降低整体部署成本。

需要注意的是，虽然量化带来了很多好处，但也可能导致模型精度的损失。因此，在使用量化之前，建议进行详细的评估和测试，以确保模型的效果满足特定应用的需求。

2. 从ResNet看数据类型的传递

2.1 从torch里面导出一个ResNet-50模型

import torch
import torchvision.models as models

model = models.resnet50()
input = torch.randn(1, 3, 224, 224)

torch.onnx.export(model, input, "resnet50.onnx")
1
2
3
4
5
6
7

可以看出来，没有量化的模型是直接从输出一直传递FP32的数据类型到output，如下图

3. 浮点数到整数的量化中遇到的问题

PS. -128~127: int8(signed int8) 0-255: uint8(unsigned char)

1. 原始浮点数组

[-0.61, -0.52, 1.62]

2. 计算量化尺度（scale）

公式：

$$\text{scale}=\frac{\text{float\_max}-\text{float\_min}}{\text{quant\_max}-\text{quant\_min}}$$

插入数值：
$$\text{scale}=\frac{1.62-(-0.61)}{127-(-128)}=0.00874509$$

3. 量化操作

• $$-0.61÷0.00874509\approx -69.75336354$$ 取整为 $$-70$$
• $$-0.52÷0.00874509\approx -59.46193807$$ 取整为 $$-59$$
• $$1.62÷0.00874509\approx 185.24680706$$ 取整为 $$185$$

结果：[-70, -59, 185]

4. 截断

由于最大整数值为127，因此185需要被截断：
[-70, -59, 185] → [-70, -59, 127]

5. 反量化

• (-70 \times 0.00874509 = -0.6121563)
• (-59 \times 0.00874509 = -0.5199999)
• (127 \times 0.00874509 = 1.1062843)

结果：[-0.6121563, -0.5199999, 1.1062843]

6. 非对称量化(如何解决截断问题)

1. 最大绝对值对称法
2. 偏移(下面公式)
   

[-0.61, -0.52, 1.62]

Scale = (1.62 - (-0.61)) / (127 - (-128)) = 0.00874509 (计算Sacle)

Z = 127 - (1.62/ 0.00874509) = -58.2468070655 = -58 (计算偏移量)

Q(1.62) = (1.62 / 0.00874509 + (-58)) = 127.246807065 = 127 (计算1.62对应的int8)

Q(-0.52) = (-0.52 / 0.00874509 + (-58)) = -117.46193807 = -117 (计算-0.52对应的int8)

Q(-0.61) = (-0.61 / 0.00874509 + (-58)) = -127.753427352 = -128 (计算-0.52对应的int8)

加了截距对应的[-70, -59, 185] --> [-128, -117, 127]

R(1.62) = (127 - (-58)) * 0.00874509 = 1.61784165

R(-0.52) = (-117 - (-58)) * 0.00874509 = -0.51596031

R(-0.61) = (-128 - (-58)) * 0.00874509 = -0.6121563

量化结果: [-0.61, -0.52, 1.62] -> [-0.6121563, -0.51596031, 1.61784165]

非对称量化代码

import numpy as np

# 截断操作
def saturate(x, int_max, int_min):
    return np.clip(x, int_min, int_max)

# 计算缩放和偏移量
def scale_z_cal(x, int_max, int_min):
    scale = (x.max() - x.min()) / (int_max - int_min)
    z = int_max - np.round((x.max() / scale))
    return scale, z

# 量化
def quant_float_data(x, scale, z, int_max, int_min):
    xq = saturate(np.round(x / scale + z), int_max, int_min)
    return xq

# 反量化
def dequant_data(xq, scale, z):
    x = ((xq - z) * scale).astype('float32')
    return x

if __name__ == '__main__':
    # np.random.seed(0)
    data_float32 = np.random.randn(3).astype('float32')
    # data_float32 = np.random.randn(100).astype('float32')
    # data_float32[99] = 100
    # data_float32 = np.array([-0.61, -0.52, 1.62], dtype='float32')
    print(f"input: {data_float32}")
    
    # uint8 bound
    # int_max = 255
    # int_min = 0
    
    # int8 bound
    int_max = 127
    int_min = -128
    
    scale, z = scale_z_cal(data_float32, int_max, int_min)
    print(f"scale: {scale}, z: {z}")
    data_int8 = quant_float_data(data_float32, scale, z, int_max, int_min)
    print(f"quant: {data_int8}")
    data_dequant_float = dequant_data(data_int8, scale, z)
    print(f"dequant: {data_dequant_float}")
    print(f"diff: {data_dequant_float - data_float32}")

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

4. 对称量化(没有截距)

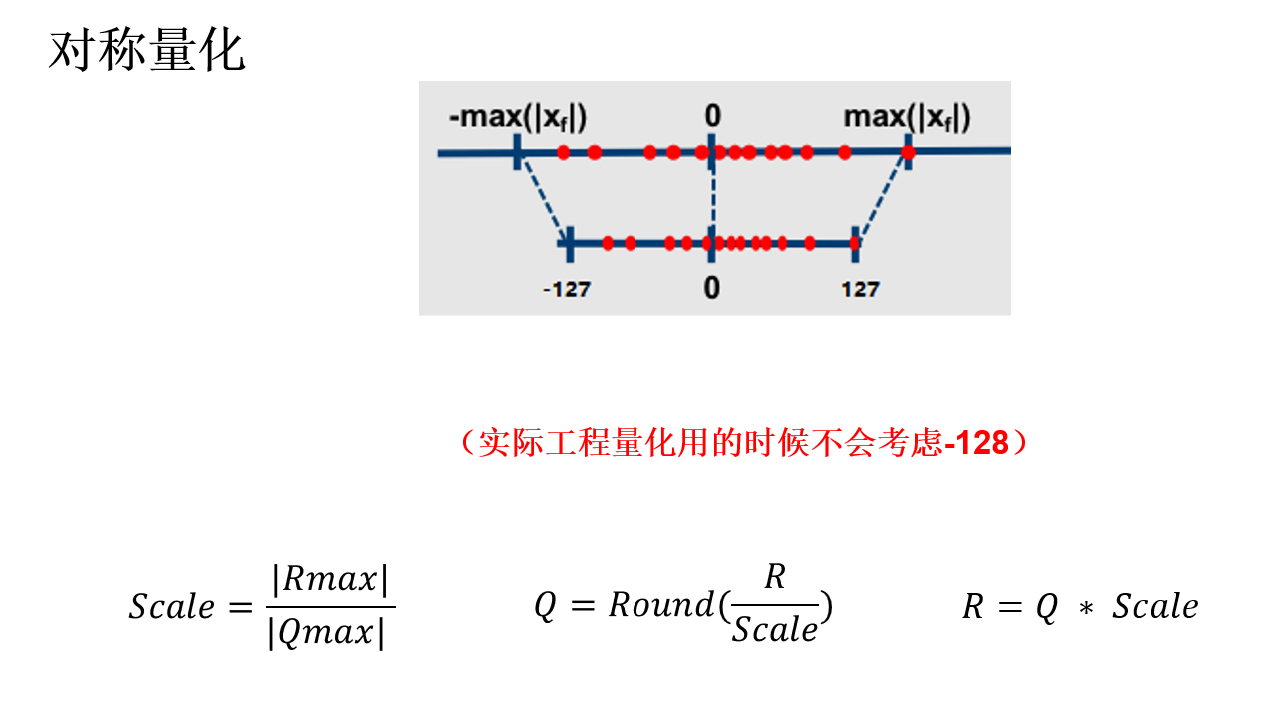
原始数组 [-1.62, -0.61, -0.52, 1.62]

scale = (1.62 / 128) = 0.01265625

Q(-1.62) = -1.62 / 0.01265625 = -128

R = -128 * 0.01265625 = -1.62

其他同理

import numpy as np

# 截断操作
def saturate(x):
    return np.clip(x, -127, 127)

# 缩放
def scale_cal(x):
    max_val = np.max(np.abs(x))
    return max_val / 127

# 量化
def quant_float_data(x, scale):
    xq = saturate(np.round(x / scale))
    return xq

# 反量化
def dequant_data(xq, scale):
    x = (xq * scale).astype('float32')
    return x

if __name__ == '__main__':
    np.random.seed(4)
    # data_float32 = np.random.randn(3).astype('float32')
    data_float32 = np.array([1.62, -1.62, 0, -0.52, 1.62], dtype='float32')
    print(f"input: {data_float32}")
    scale = scale_cal(data_float32)
    print(f"scale: {scale}")
    data_int8 = quant_float_data(data_float32, scale)
    print(f"quant: {data_int8}")
    data_dequant_float = dequant_data(data_int8, scale)
    print(f"dequant: {data_dequant_float}")
    print(f"diff: {data_dequant_float - data_float32}")

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34