线性代数中涉及到的matlab命令-第一章：行列式

目录

1，逆序数 

2，行列式定义和性质

2.1，常用特性及命令 

2.2，求行列式

2.3，行列式的性质 

2，行列式按行（列）展开 

3，范德蒙德行列式

---

 

在学习线性代数过程中，发现同步使用MATLAB进行计算验证可以加深对概念的理解，并能掌握MATLAB的命令和使用方法；

使用的线性代数教材为同济大学出版的。 

1，逆序数 

没有找到对应的Matlab命令，但可以通过简单编程来进行求解；

2，行列式定义和性质

需要注意的是，在MATLAB中运算时直接使用矩阵表示行列式；

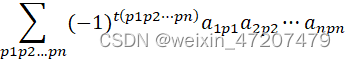
2.1，常用特性及命令 

转置 B = A'

上三角、下三角行列式：

使用的Matlab命令，tril和triu

2.2，求行列式

det(A)

2.3，行列式的性质 

以下为利用matlab的det命令对行列式的几种性质进行计算： 

上三角矩阵的行列式为对角线元素的乘积：

对角矩阵行列式为对角线元素的乘积：

性质1，行列式和它转置后的行列式相等：

性质2，交换矩阵的两行（列），行列式变号：

 推论，矩阵中存在相同的行或列，则行列式等于0（可以用上一条进行推倒）：

性质3，矩阵的一行或列所有元素乘以k，其行列式也乘以k：

性质4，行列式中如果有两行（列）元素成比例，则行列式等于0：

 

性质5，

clc;
 
A=[2 4 6 7;
   1 3 2 1;
   1 5 7 3;
   1 2 1 5];
 
B=[2 4 2 7;
   1 3 2 1;
   1 5 3 3;
   1 2 0 5];
 
C=[2 4 4 7;
   1 3 0 1;
   1 5 4 3;
   1 2 1 5];
 
D_A = det(A)
 
D_B = det(B)
 
D_C = det(C)

 运行结果：

性质6，矩阵的一行或列加上另一行或列的k倍，行列式的值不变：

行列式性质例10证明，具体的证明请查阅教材：

使用Matlab计算一个这样的实例：

clc;
a = [ 1 2;
      3 4];
b = [0 0 0;
     0 0 0];
c = [6 7;
     4 5;
     2 7];
d = [3 6 2;
     8 5 3;
     4 6 2];
 
e = [a,b];
f = [c,d];
 
A = [e;f]
 
D_A = det(A)
 
D_a = det(a)
 
D_b = det(d)

运行结果：

可见D(A) = D(a)*D(d)。 

2，行列式按行（列）展开 

余子式和代数余子式：

%求N(2,1)的余子式和代数余子式
clc;
 
N = [3 6 2 5;
     8 5 3 7;
     4 6 2 9;
     5 7 4 1];
 
N(2,:) = [];      %把第二行划去
N(:,1) = [];      %把第一列划去
 
N
 
M_21 = det(N)                  %余子式
 
A_21 = (-1)^(2+1)*det(N)       %代数余子式

运行结果：

 对上边引理计算一个对应的Matlab程序：

clc;
 
A=[2 4 6 7;
   0 3 0 0;
   1 5 7 3;
   1 0 1 0];    %A的第二行除A(2,2)外全为0
 
B = A;
 
B(2,:) = [];
B(:,2) = [];   %A的第二行第二列的余子式
 
D_A = det(A)
 
%D_B = det(B)
D_B = (-1)^(2+2) * det(B)  %A的第二行第二列的代数余子式

运行结果与引理相符：

对上边定理计算一个对应的Matlab程序： 

clc;
 
A=[2 4 6 7;
   1 3 2 1;
   1 5 7 3;
   1 0 1 0];
 
B = A;
C = A;
D = A;
E = A;
 
B(2,:) = [];
B(:,1) = [];   %A的第二行第一列的余子式
 
C(2,:) = [];
C(:,2) = [];   %A的第二行第二列的余子式
 
D(2,:) = [];
D(:,3) = [];   %A的第二行第三列的余子式
 
E(2,:) = [];
E(:,4) = [];   %A的第二行第四列的余子式
 
 
D_A = det(A)
 
D_B21 = (-1)^(2+1) * det(B) * A(2,1) %A的第二行第一列的代数余子式 * 第二行第一列元素
 
D_C22 = (-1)^(2+2) * det(C) * A(2,2) %A的第二行第二列的代数余子式 * 第二行第二列元素
 
D_D23 = (-1)^(2+3) * det(D) * A(2,3) %A的第二行第三列的代数余子式 * 第二行第三列元素
 
D_E24 = (-1)^(2+4) * det(E) * A(2,4) %A的第二行第四列的代数余子式 * 第二行第四列元素

运行结果与定理相符：

3，范德蒙德行列式

 以下程序产生一个范德蒙德行列式并分别用det和 的方式计算行列式的值：

clc;
 
v = 2:0.5:4;
 
A = vander(v);
 
A = fliplr(A);
 
A = A'
 
D_A = det(A)
 
tot =(A(2,5)-A(2,4)) * (A(2,5)-A(2,3)) * (A(2,5)-A(2,2)) * (A(2,5)-A(2,1)) * (A(2,4)-A(2,3)) * (A(2,4)-A(2,2)) * (A(2,4)-A(2,1)) *...
     (A(2,3)-A(2,2)) * (A(2,3)-A(2,1)) * (A(2,2)-A(2,1))

运行结果：

上图中第二个计算结果是通过 方式计算。