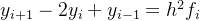二阶常微分方程的显隐求解格式

• 本文介绍的这两个格式相容性都比较低，不建议使用，写作本文的目的是提醒大家使用换元法把高阶方程转换成一阶常微分方程组求解  
• 全代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
 
 
#Second-Order Differential Equation
#y''(x) = f(x, y)
class SODE():
    def __init__(self, f, X_start=0, X_end=1, Y_start=1, dY_start=1, ddY_start=1, h=0.01):
        self.f = f
        self.h = h
        self.X = np.arange(X_start, X_end, self.h)
        self.Y = np.zeros(self.X.size)
        self.Y[0] = Y_start
        self.Y[1] = Y_start + self.h * dY_start + 0.5 * self.h**2 * ddY_start
        self.tol = 1e-6
 
    def Stormer(self, ):
        for i in range(2, self.X.size):
            self.Y[i] = self.h**2 * self.Y[i-1] + 2 * self.Y[i-1] - self.Y[i-2]
        return self.Y
    
    def Cowell(self, ):
        for i in range(2, self.X.size):
            self.Y[i] = 1/(1-self.h**2/12) * ((10*self.Y[i-1]+self.Y[i-2])*self.h**2/12 + 2*self.Y[i-1] - self.Y[i-2])
        return self.Y
    
c = SODE(f = lambda x,y:x + y)
y1 = c.Stormer()
y2 = c.Cowell()
plt.plot(c.X, y1, label="Stormer")
plt.plot(c.X, y2, label="Cowell")
f = lambda x:0.5*np.exp(-x)*(-1+3*np.exp(2*x)-2*x*np.exp(x))
y3 = f(c.X)
plt.plot(c.X, y3, label="True")
plt.legend()
plt.pause(0.01)
 

• Stormer 公式

• Cowell 公式

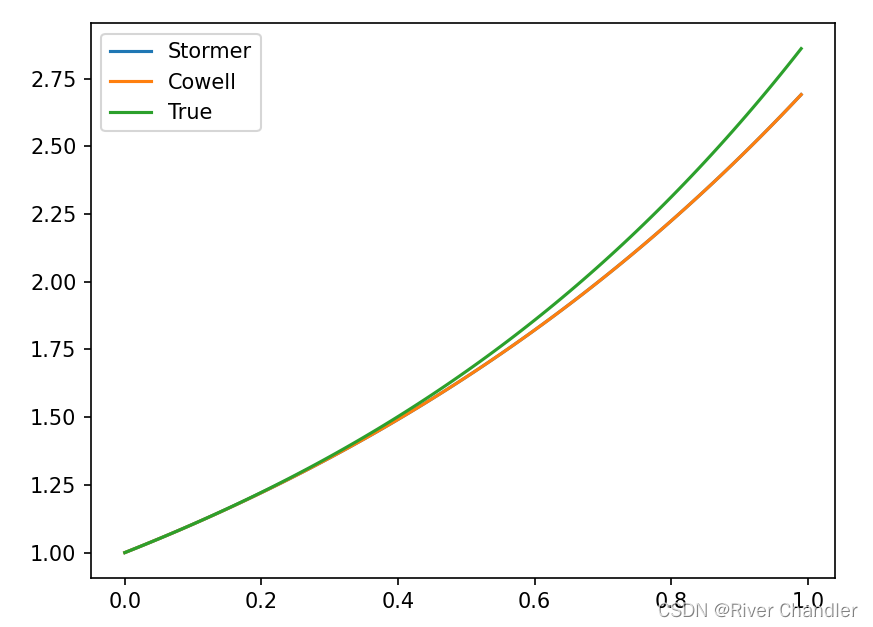
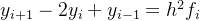
• 当然我们也可以自己微操，比如Stormer 公式就是二阶导数的近似公式，只要取得点足够多，初始猜测的点足够多，就能自己创造公式，不过用处不大了！