数据结构--排序（2）

前言

排序（1）链接入口
快速排序 链接入口

归并排序

思想：将数组利用递归形式一直对半平分，将一组完整的数组分成若干份，

接着将它们相邻两个分为一组，进行排序，排序之后组合成一组，一直往复，最终将它们合起来，完成排序。

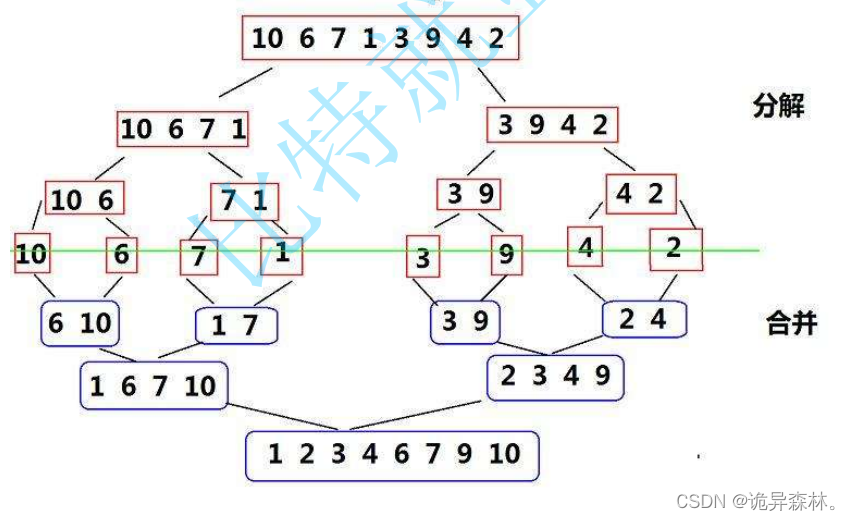
代码思路：我们可以分为两部分，分解和合并；
这种方法我们采用递归的方法来实现最为合适；分解到一个元素一个单位，再将它们两两合一；
在合并过程中，需要一个中间数组来暂存已经排好的数据，否则排好是数据无法保存；

void _MergeSort(int* a, int* tmp, int begin, int end)
{
	//先将它们分开
	//终止条件
	if (begin >= end)
	{
		return;
	}
	int mid = (begin + end) / 2;
	
	_MergeSort(a, tmp, begin, mid);//不能取mid-1
	_MergeSort(a, tmp, mid+1, end);//不能取mid

	//归并排序
	int begin1 = begin, end1 = mid;
	int begin2 = mid+1, end2 = end;
	int index = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[index++] = a[begin1++];
		}
		else
		{
			tmp[index++] = a[begin2++];
		}
	}
	//会有一组先排完，另一组接着放入tmp
	while (begin1 <= end1)
	{
		tmp[index++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[index++] = a[begin2++];
	}
	//将排好的数返回a数组中
	memcpy(a+begin, tmp+begin, (end - begin + 1) * sizeof(int));
	
}
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(n * sizeof(int));
	if (tmp == NULL)
	{
		perror("MergeSort tmp malloc fail");
		exit(-1);
	}

	_MergeSort(a, tmp, 0, n - 1);

	free(tmp);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

tmp就是中间数组，begin和end都表示下标；
这里需要注意，mid所取的数是偏左的，如对于两个元素和三个元素，由于符号/，算出来的mid均为1，如果对于函数_MergeSort()的参数begin也取mid，就有可能陷入死循环，

接着就是归并排序了，用memcpy函数将中间函数的值转过来；

非递归方法

我们也可以利用循环的方式实现对数组进行分组，用一个变量gap将它们进行分段；然后再加上一个循环，在每个段内进行排序；最终进行合并。

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("MerSort malloc fail");
		exit(-1);
	}
	int gap = 1;
	//gap分段，gap会变大
	while (gap < n)
	{
	//在被gap分段的数组中进行排序
		for (int i = 0; i < n; i += gap * 2)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = gap + i, end2 = i + gap * 2 - 1;
			
			
			int index = i;
			//判断边界是否越界
			
			if (begin2 >= n)
			{
				break;
			}
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}
			//会有一组先排完，另一组接着放入tmp
			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}
			//将排好的数返回a数组中
			memcpy(a + i, tmp + i, (end2-i+1 ) * sizeof(int));
		}
		gap*=2;
	}
	free(tmp);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

对于分段所处下标，end1，begin2，end2均有可能会超过n，所以需要进行判断；

对于end1越界和begin2越界，两种都不需要进行排序，且end1越界被包含在begin2越界，所以直接判断begin2越界break；
end2越界需要进行排序；

验证：

void TestMergeSort()
{
	int a[] = { 9,1,2,5,7,4,8 ,6,3,5,1,2,3,5,1,8,3 };
	MergeSort(a,  sizeof(a) / sizeof(a[0]));
	PrintfArray(a, sizeof(a) / sizeof(a[0]));
	
}

void TestMergeSort2()
{
	int a[] = { 9,1,2,5,7,4,8,6,3,5,1,2,3,5,1,8,3 };
	
	MergeSortNonR(a, sizeof(a) / sizeof(a[0]));
	PrintfArray(a, sizeof(a) / sizeof(a[0]));

}
int main()
{
	

	TestMergeSort();
	TestMergeSort2();
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

时间复杂度：O(N*logN)
空间复杂度：O(N)

计数排序

思想：通过对数组元素的大小，将它们记录在对应的另一组数组中，将它们从小到大有序的统计在另一个数组中；一个数字对应一个下标；

然后将它们加上最小值填回原数组中，即可完成排序。

void CountSort(int* a, int n)
{
	
	//找出最大数和最小数
	int max = a[0], min = a[0];
	for (int i = 0; i < n; i++)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}

	int* Range = malloc(sizeof(int) * (max-min+1));
	if (Range == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	//初始化
	memset(Range, 0, sizeof(int) * (max-min+1));
	//先将数据录入
	for (int i = 0; i < n; i++)
	{
		Range[a[i] - min]++;
	}
	//排序
	int index = 0;
	for (int i = 0; i < max-min+1; i++)
	{
		int j = Range[i];
		while (j--)
		{
			a[index++] = i + min;
		}
			
	}
		
	
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

这种排序适合一些小众的场景中；
如相对集中的整数数组，像0，99999这样的话就开辟数组有点大，浪费空间；
初特征就有对应数字了（ASCII码值，整数数字）。

时间复杂度：O(MAX(N,范围))
空间复杂度：O(范围)