【1++的刷题系列】之双指针

👍作者主页：进击的1++
🤩 专栏链接：【1++的刷题系列】

一，什么是双指针

常见的双指针有两种形式：一种是对撞指针（也称为左右指针）；另一种是快慢指针。

对撞指针从两指针向中间移动，一个指针在最左端，一个在最右端，逐渐向中间移动。
其终止条件一般是两指针相遇或错开，或是得到结果，直接跳出内部循环。

快慢指针的基本原理就是两个速度不同的指针在数组或链表上移动。
这种方法处理环形链表或数组是非常有用的。不单单是环形链表或数组，处理循环往复的情况时我们都可以用快慢指针来解决。
最常用的一种快慢指针就是快指针走两步，慢指针走一步。

二，相关例题

例一

题解：
我们通过题目可以知道，这道题涉及到了数组内部元素的移动，因此我们想到用双指针的解法。
再仔细分析题目我们可以看到，题目中是要将0元素全部放在最后，并且非0 元素的相对位置不能改变，因此我们想到用快慢指针的方法来解决。
下面我们展示两种快慢指针的思路。

解法一：

lass Solution {
public:
    void moveZeroes(vector<int>& nums) 
    {
        //快慢指针
        if(nums.size()==1 || nums.empty())
            return ;

            int right=1;
            int left=0;
            while(right<nums.size()&&left<nums.size())
            {
                while(right<nums.size() && nums[right]==0)
                {
                    right++;
                }
                if(right>=nums.size())//对没有0时的处理
                    break;

                while(nums[left]!=0 && left<right)
                {
                    left++;
                }

                swap(nums[right],nums[left]);
                right++;

            }

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

我们可以将数组分为三部分：非0区—0区–待处理区。
接着我们定义left,right指针。分别为一慢，一快。0-left是非0区；left-right是0区；right–结束 是待处理区。
通俗点就是left指针找0，right指针找非0 。然后两指针所指向内容进行交换。（要注意的是while循环条件的写法，防止数组越界）
最终该解法时间复杂度为O(n),空间复杂度为O(1)。

解法二：

class Solution {
public:
    void moveZeroes(vector<int>& nums) 
    {
        int left=-1;
        int right=0;
        for(;right<nums.size();right++)
        {
            if(nums[right])
            {
                swap(nums[++left],nums[right]);
            }
        }

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

在这种解法中也是将数组划分为了上述的三个区域。left指向的是非0区的最后一个元素，而right则是向前找非0元素。然后与left的前一个元素（即0）进行交换。时间复杂度与空间复杂度与解法一相同，就是该方法更为简洁，不需要考虑特殊情况。

例二

本题也是对数组内部的元素进行移动，因此我们想到能够用双指针的写法来解决。
本题的暴力解法就是：再创建出一个数组，遍历原来的数组进行复写。但显然这种方法空间复杂度过高。
因此我们想如何能够在本数组内进行操作。若是从前往后我们用快慢指针来进行复写，则会将数组中原来的值遮盖。所以不行！因此我们考虑从后往前的可行性。我们发现后面的一些元素是再进行复写后将要被舍弃掉的。因此我们只需要找到需要复写后数组的最后一个元素，将复写要数组的最后一个元素移到数组最后。。。。这样就可以实现双指针了。

class Solution {
public:
    void duplicateZeros(vector<int>& arr) 
    {
      //找最后一个位置
      int right=-1;
      int cur=0;
      int n=arr.size();
      while(cur<n)
      {
          if(arr[cur]) right++;
          else
            right+=2;
        if(right>=n-1)
            break;
         
         cur++;

      }

      //调整
      if(right==n)
      {
          arr[n-1]=0;
          cur--;
          right-=2;
      }


      while(cur>=0)
      {
          if(arr[cur])
          {
              arr[right--]=arr[cur--];
          }
          else{
              arr[right--]=0;
              arr[right--]=0;
              cur--;
          }
      }


    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

本题中要注意的是两点：一是如何去找复写后最后一个元素；二是对于特殊情况的处理。
找最后一个元素我们通过模拟复写的过程的寻找，定义一个指向最后复写数的指针cur,模拟复写位置的指针right。则cur遇到0，right走两步，否则走一步，知道right超过数组大小。
对于特殊情况：出现这种情况的原因是，当复写的最后一个元素是0时，其可能由于数组已经到最后的原因不会写两次，但是我们在模拟找复写元素位置的时候却没有去考虑这种情况，因此此时的right会超过数组的大小。因此在中间步骤我们进行了纠正。

例三

我们分析题目，发现结果只有两种：变为1和无限循环但变不到1 。
对于循环的情况，我们就可以想到用快慢指针，一个追一个，若是在循环圈里快的追上慢的，则跳出，进行判断终止的数字是否为1 。

class Solution {
public:
 
    //求和
    long long bitsum(int n)
    {
        long long sum=0;
        while(n)
        {
            int x=n%10;
            sum+=x*x;
            n/=10;
        }
        return sum;
    }

    bool isHappy(int n) 
    {
        long long slow=n;
        long long fast=bitsum(n);
        while(slow!=fast)
        {
            slow=bitsum(slow);
            fast=bitsum(bitsum(fast));
        }

        if(slow==1)
        return true;
        else
        return false;
        
    }  

    
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

例四

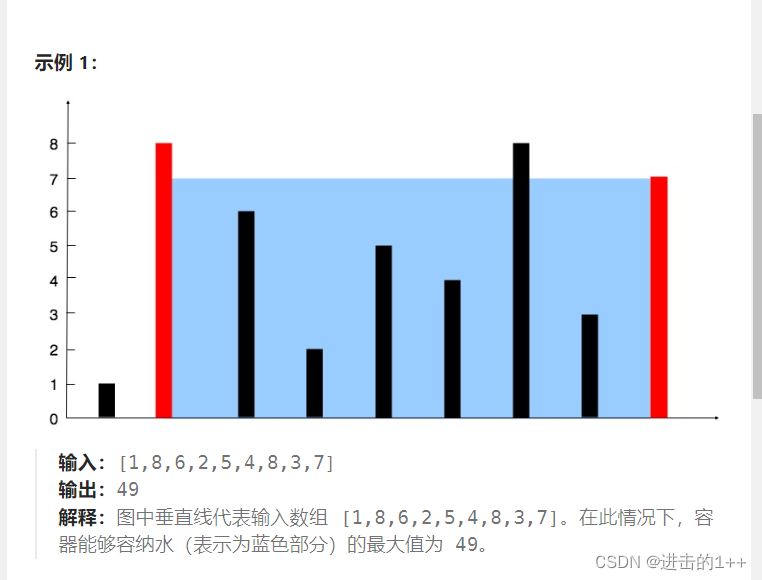
我们来分析题目：
求容器的体积，无非就是求长，宽，高。这里宽是固定的，所以我们只需要考虑长和高。其高是有数组的长度决定的，高则是由数组两端的最小值决定的。
首先是暴力解法：
固定一端然后遍历一遍数组，直到所有情况被枚举出来。该方法时间复杂度为O(n^2),因此我们不采用。我们再进行观察：若是我们设数组的长依次降低，那么只有当其高度比现在的高度要高时，该体积才可能会增大。并且高由最短的一端决定，因此我们在数组的两端设两个指针，每次让指向最小值的那个指针进行遍历。我们就能够得出最大值了。

class Solution {
public:
    int maxArea(vector<int>& height) 
    {
        int left=0;
        int right=height.size()-1;
        long long ret=0;
        while(left<right)
        {
           long long Min=min(height[left],height[right]);
            long long v=Min*(right-left);
            ret=max(ret,v);
            if(height[right]>height[left])
            {
                left++;
            }
            else
            right--;
        }

        return ret;

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

例五

对于三角形来说，两条较短边的和若是大于第三边，则构成三角行。
若此题使用暴力解法，则需要从小到达列举所有的三元组，统计满足条件的三元组，这种方法的时间复杂度过高。达到了O(n^3) 。因此不可取。接下来我们进行优化。
**两条较短边的和若是大于第三边，则构成三角行。**涉及到最大的边的问题我们不妨将数组进行升序的排序。我们先固定一个最大的边，再在左右两端定义两个指向较短边的指针。若左右两端指针所指元素之和大于固定的第三遍，则这两个指针的区间内所有的元素均可以构成。再将右指针向左移，继续统计；若不大于，则做指针想右移。。。
直到固定的这个最大的边都匹配完，则指向最大的边的指针左移，继续上述操作。
这样我们的时间复杂度就降为了O(n^2) 。

class Solution {
public:
    int triangleNumber(vector<int>& nums) 
    {
        if(nums.size()<3) return 0;
        sort(nums.begin(),nums.end());
        //固定最大的一端
        int ret=0;
        for(int i=nums.size()-1;i>=2;i--)
        {
            int right=i-1;
            int left=0;
            while(right>left)
            {
                if(nums[left]+nums[right]>nums[i])
                {
                    ret+=right-left;
                    right--;
                }
                else
                {
                    left++;
                }
            }
        }

        return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29