-
AB试验(四)基于规范流程的一个案例分析
AB试验(四)基于规范流程的一个案例分析
确定目标和假设
- 业务场景:某音乐APP,通过历史数据发现一些便利功能往往有着较高的留存和续订。但是这些便利功能的使用率并不高。调研发现,由于APP崇尚简洁设计,因此这些功能会放在每首歌曲的功能列表中,用户发现或使用都不容易。
- 目标:通过以上业务现状,团队需要增加用户对产品功能的使用率
- 脑暴解决方案:
- 将每个功能直接显示出来,这样用户就会一目了然,但是过多的功能铺成使得界面看起来极其糟糕,用户体验较差
- 新用户注册登录时进行功能引导,但是新用户刚使用时并不会使用所有和功能,大多会选择快速跳过
- 在用户有需求的时候,通过弹窗形式告知用户使用相关功能。
- 假设:只在用户有需求的时候弹窗引导用户使用相关功能,可以提高相关功能的使用率
确定指标
- 定义场景:团队准备以“把喜欢的音乐加入收藏夹”这个功能做一个A/B测试
- 定义触发条件:用户从未使用过这个功能,且播放同一首歌到达x次时,进行弹窗提醒
- 数据分析优化场景
- 历史数据分析确定x的最优值为4。即用户从未使用过这个功能,且播放同一首歌到达4次时,在播放第5次进行弹窗提醒可以把喜欢的音乐加入收藏夹
- 由于弹窗仅是对用户的提醒,因此不做重复弹窗,所以每个符合条件的用户最多只能收到一次弹窗
- 定义评价指标
- 评价指标:【把喜欢的音乐加入收藏夹】功能的使用率=使用了【把喜欢的音乐加入收藏夹】的用户总数/实验中的用户总数
- 定义实验用户:所有符合触发条件的用户,并将该用户随机分配至实验/对照组
- 定义时间窗口:用户收到弹窗到最终使用功能的时间分布可能较分散(例如1天,2天甚至1个星期),由于实验周期可能超过一天,因此需要规定好统一的时间窗口,如弹窗后x天内使用率。由于该业务场景关注的是及时性,因此可以设为弹窗后1天内使用率。
- 优化评价指标:【把喜欢的音乐加入收藏夹】功能的使用率=弹窗后1天内使用了【把喜欢的音乐加入收藏夹】的用户总数/实验中的用户总数,且用户符合触发条件。
- 通过历史数据的回溯分析,得到用户在符合触发条件后一天内使用把喜欢的音乐加入收藏夹】功能的概率为2%,通过统计公式计算得到置信区间为[1.82%,2.18%]。
确定实验单位
由于弹窗对用户是易于感知的变化,因此为了保证用户体验的连贯性,这里选择用户为最小的实验单位,具体的为用户ID
样本量估算
-
设置 α = 5 % \alpha=5\% α=5%, p o w e r = 80 % power=80\% power=80%,所以 n ≈ 8 σ p o o l e d 2 δ 2 n \approx \frac{8\sigma_{pooled}^2}{\delta^2} n≈δ28σpooled2
-
δ = 2.18 % − 2 % = 0.18 % ≈ 0.2 % \delta = 2.18\%-2\% = 0.18\% \approx 0.2\% δ=2.18%−2%=0.18%≈0.2%
-

-
计算 n = 80000 n=80000 n=80000,实验为50%-50%,所以需要的总体用户约为16万
随机分组
-
采取CR算法对用户随机分组
-
由于同类型的实验有多个,避免实验间的干扰,申请B-1层的流量进行此次【把喜欢的音乐加入收藏夹】的A/B测试
-
设计实验过程
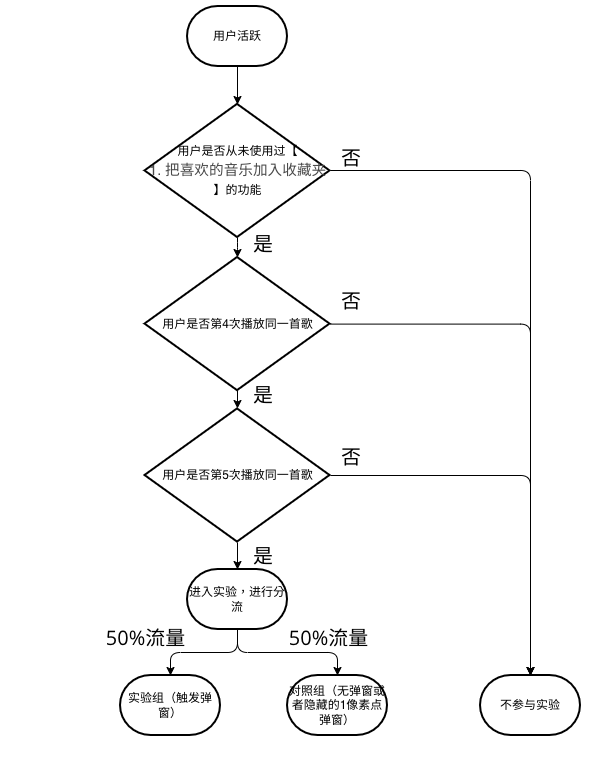
测算时间的估算
- n = 16.4 w n=16.4w n=16.4w,每天符合触发条件的用户约1.7w。因此本实验大约需要10天
- 考虑到周末和工作日用户活跃的差异,因此需要至少包括一整个周。由于上述计算的最小周期为10天包含了一周,所以本次实验的周期定为10天
实施测试
- 实验伊始,给予该层1%的流量进行观察,运行过程产品端,数据埋点,用户反馈均无明显异常
- 逐渐增大至全部流量,整个实验进行顺利
分析测试结果
-
收集数据:在10天后,收集到实验组样本80723,符合触发条件一天内使用该功能的用户3124;对照组样本80689,符合触发条件一天内使用该功能的用户1598。达到最小样本量。
-
分析统计层面的护栏指标
- 实验对照组样本比例:实验组样本是80723,对照组样本是80689。由于等流量分组,因此样本进入实验组的概率 p = 0.5 p=0.5 p=0.5,则 S E = 0.5 ( 1 − 0.5 ) 80723 + 80689 = 0.12 % SE=\sqrt{\frac{{0.5}(1-{0.5})}{80723+80689}}=0.12\% SE=80723+806890.5(1−0.5)=0.12%。则进入实验组的置信区间为 [ 0.5 − 1.96 ∗ 0.12 % , 0.5 + 1.96 ∗ 0.12 % ] = [ 49.76 % , 50.24 % ] [0.5-1.96*0.12\%, 0.5+1.96*0.12\%]=[49.76\%,50.24\%] [0.5−1.96∗0.12%,0.5+1.96∗0.12%]=[49.76%,50.24%]。实验组/对照组的实际占比分别为50.01%、49.99%。符合样本比例合理检验。
-
实验对照组主要特征分布是否相似:通过ks检验,两组的分布基本一致(假设进行了此操作)
-
通过z检验,得到p值接近于零,远小于5%。同时计算评价指标差值(1.89%) δ \delta δ的95%置信区间为[1.72%,2.05%],不包括0。事实证明在用户需要的时候进行弹窗提醒确实有效
-
后续将陆续推广其他相关功能的推广
总结
当你熟练的时候,一次A/B试验是很简单的~
共勉~
-
相关阅读:
2023-11-18 mysql-sysbench压测TPS/QPS-记录
【数据库】实验五 数据库综合查询|多表查询、聚集函数、orderby、groupby
呼叫中心系统解决方案有哪些
【数据结构与算法】03 队列(顺序队列--循环队列--优先级队列--链队列)
Leetcode力扣 MySQL数据库 1841 联赛信息统计
js添加 删除 替换 插入节点所用的方法。js常用的几种事件。
UMA 2 - 创建自己的UMA模型⭐一.配置Blender环境
jQuery中显示与隐藏
【国标语音对讲】EasyCVR视频汇聚平台海康/大华/宇视摄像头GB28181语音对讲配置
你要了解,哪些财产不属于夫妻共同财产
- 原文地址:https://blog.csdn.net/weixin_39293132/article/details/133275447