[python 刷题] 853 Car Fleet

[python 刷题] 853 Car Fleet

哎……周赛第三题解应该用 monotonic stack 做优化的，没写出来，所以多刷两题 monotonic stack 的题目找找感觉……

题目：

There are n cars going to the same destination along a one-lane road. The destination is target miles away.

You are given two integer array position and speed, both of length n, where position[i] is the position of the ith car and speed[i] is the speed of the ith car (in miles per hour).

A car can never pass another car ahead of it, but it can catch up to it and drive bumper to bumper at the same speed. The faster car will slow down to match the slower car’s speed. The distance between these two cars is ignored (i.e., they are assumed to have the same position).

A car fleet is some non-empty set of cars driving at the same position and same speed. Note that a single car is also a car fleet.

If a car catches up to a car fleet right at the destination point, it will still be considered as one car fleet.

Return the number of car fleets that will arrive at the destination.

如果车碰撞在一起的话，就会融合成一个 cluster，这题问的是到了终点后会有几个 cluster

几个核心重点是：

• 所有车共用一条道
• 永远不可能超车
• 后车撞到前车，后车速会降到前车的速度
• 两车之间没有间距

以第一个例子 target = 12, position = [10,8,0,5,3], speed = [2,4,1,1,3] 来说，图解大概是这个样子的：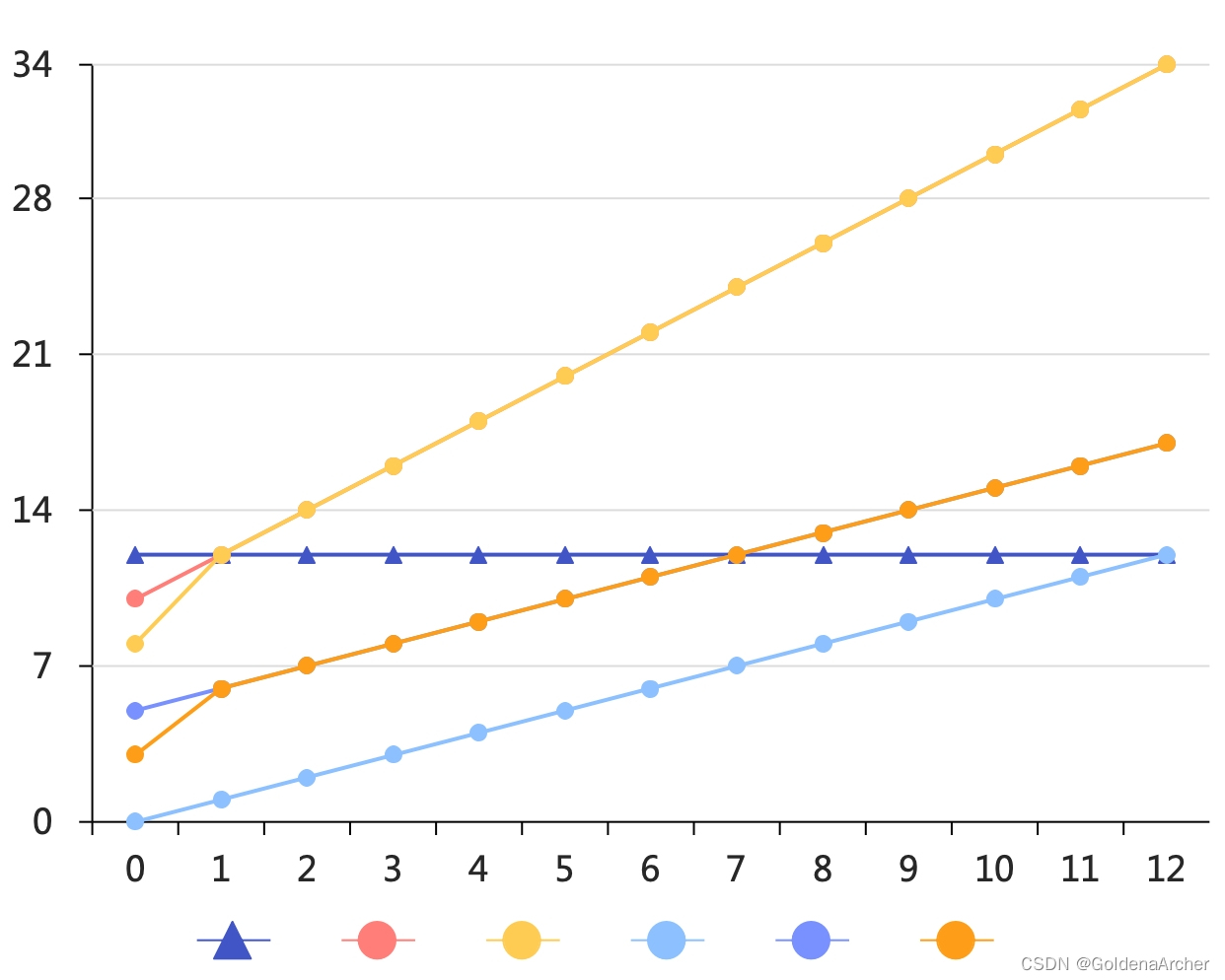

图解其实能够比较明显的看出有几个 cluster

这道题的一个解法是使用 monotonic stack 去做，思路大致如下：

1. 构成 [position, time] 的配对

2. 对 position 使用降序排序

   因为有一个 target 的限制，所以这道题会出现这两种情况：

   1. 两辆车会在抵达 target 之前/之时相遇

      这也就意味着初始位置较小的那一条在 $0<=t<=target$ 这个时间段之间会遇到初始位置较大的那一条

      这个时候，初始位置较大的那辆车相当于作为距离和速度的上限，两辆车相遇后即可合并为一个 cluster，并且依旧以初始位置较大且速度较慢的那辆车作为上限

      其原因就在于 后车撞到前车，后车速会降到前车的速度 这条限制，换言之，一旦相遇后，两辆车其实就可以视为一辆车

   2. 两条线不会在抵达 target 之前/之时相遇

      这种情况到下一步处理

3. 完成了之后就可以对抵达速度使用 monotonic stack 进行追溯，这个时候只需要保留抵达时间耗时较久（速度较慢）的那条即可

   依旧以上面的案例进行解释，将其进行排序后的结果为：[(10, 2), (8, 4), (5, 1), (3, 3), (0, 1)]

   • 第一辆车抵达终点的时间为 1.0

   • 第二辆车抵达终点的时间也为 1.0

     这时候可以讲两辆车的抵达时间合并，并且取第一辆的抵达时间

     主要原因也是因为在初始距离较大，初始速度较慢，在抵达最终距离前/时被追上，一定意味着后车抵达最终距离的耗时 $<=$ 前车

   • 第三辆抵达终点位置的时间为 7.0

     这时候它与前车不相交，因此自成一个 cluster

   • 重复当前操作一直到遍历完所有车

使用 LC 上提供的第三个案例相对而言会更直接一些：

target = 100, position = [0,2,4], speed = [4,2,1]

代码如下：

class Solution:
    def carFleet(self, target: int, position: List[int], speed: List[int]) -> int:
        # store (speed, pos) pair
        pair = [(p, s) for p, s in zip(position, speed)]
        stack = []
        pair.sort(reverse = True)

        for p, s in pair:
            stack.append((target - p) / s)
            print((target - p) / s)
            if len(stack) >= 2 and stack[-1] <= stack[-2]:
                stack.pop()

        return len(stack)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

更新于 2023-09-30

复习这道题的时候用了一个简化版的 monotonic stack，即直接对比了一下当前耗时与 stack[-1] 的耗时，如果当前耗时 <= stack[-1]，同样也可以代表着两个数字可以合并在一个 cluster 中，因此可以舍弃当当前这个用时较快的时间，代码如下：

class Solution:
    def carFleet(self, target: int, position: List[int], speed: List[int]) -> int:
        # use res to save all the time, and thus the result
        res, cars = [], []

        # group cars by their [pos, s]
        pair = [(p, s) for p, s in zip(position, speed)]

        # sort the array by position
        cars.sort(key=lambda x: x[0], reverse=True)

        # the if faster car catches up to a slower car, it's speed is going to be reduced
        #   thus if 2 cars eventyally will meet each other, just take the slower car's speed as
        #   the time for this cluster
        for pos, s in cars:
            # calculate time used to cross finish line
            time_used = (target - pos) / s
            # slower catches faster car before/at finish line
            if res and time_used <= res[-1]:
                continue
            res.append(time_used)

        return len(res)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

本质上来说大 O 没什么区别，不过少了一些进出栈的操作，相对而言会快这么一丢丢