-
一些数学公式的几何意义
三角函数平方和公式:
三角函数中的平方和公式有三个形式:
第一种:
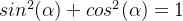 ;
;接着两边同时除以
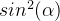 可以得到第二种:
可以得到第二种: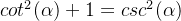 ;
;或第一种同时除以
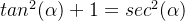 可以得到第三种:
可以得到第三种: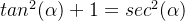 。
。
首先我们做一个单位圆,我们学三角函数的时候应该都是从单位圆开始的吧~
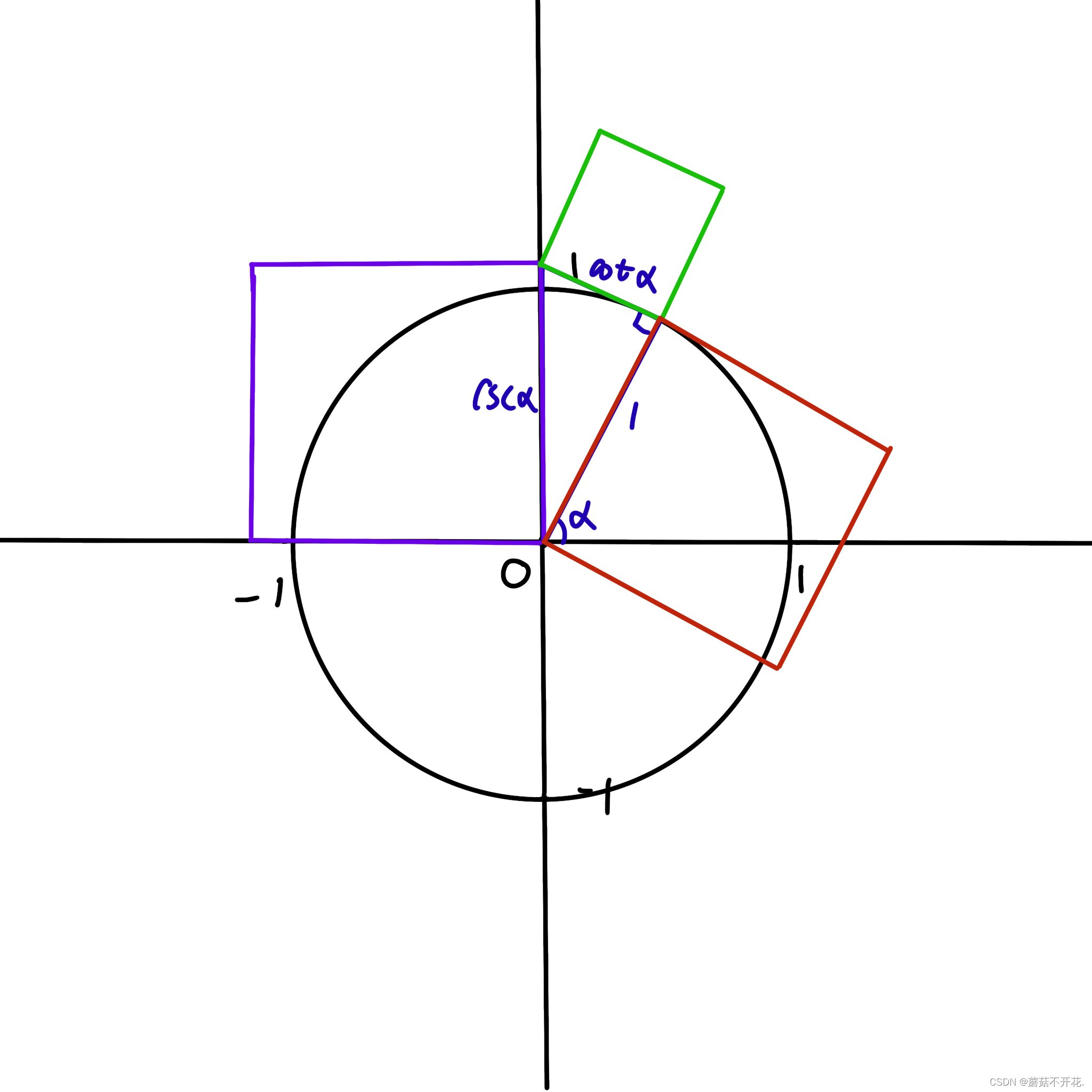
将x轴的单位“1”逆时针旋转α°,再从顶点向x轴作垂线,就可以构造一个三角形,这个三角形的三条边分别是1,sinα,cosα。
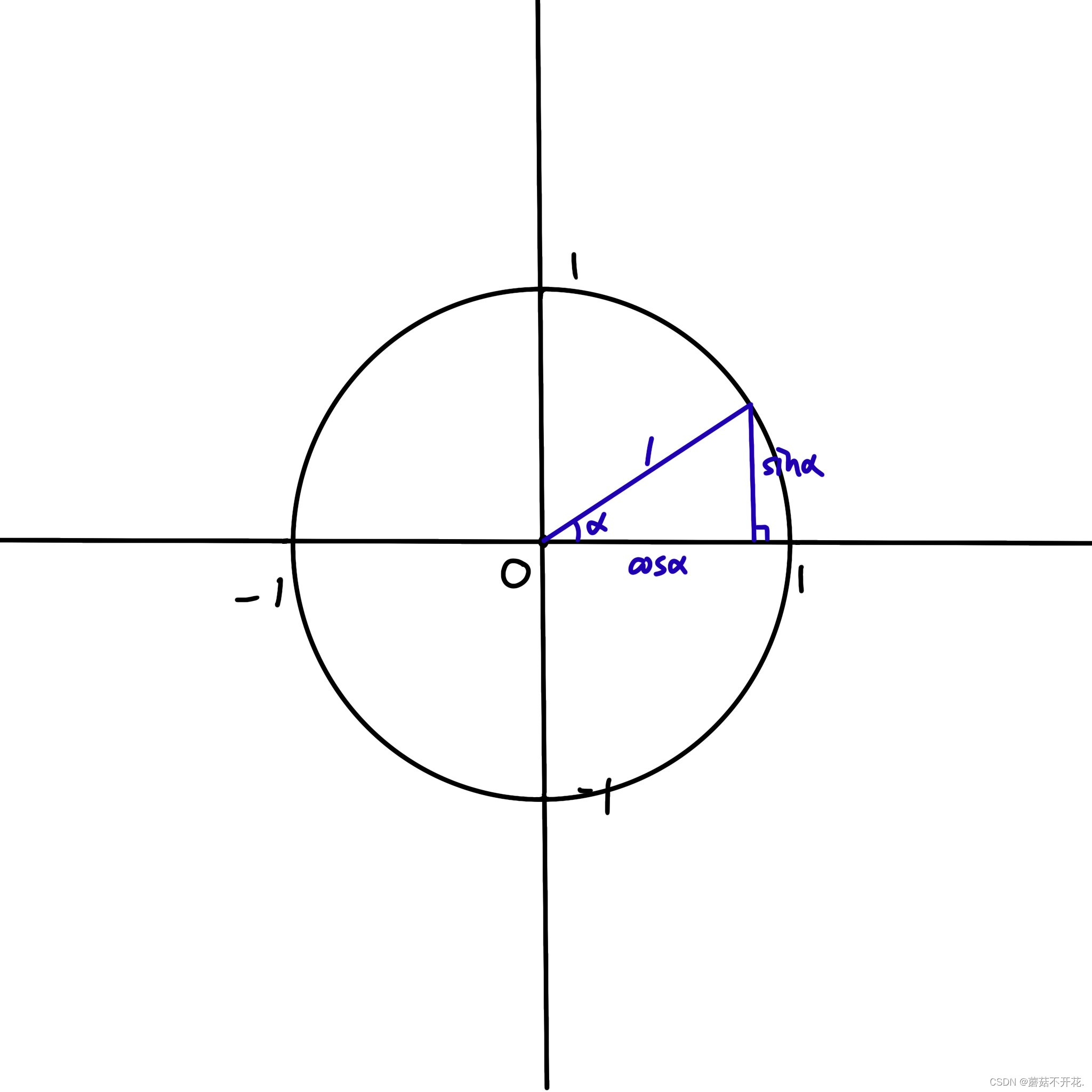
以这三条边为边长向外延伸出三个正方形。我们都学过勾股定理,易得sin²α+cos²α=1,这是第一种形式的几何意义,无论α为多少都成立。
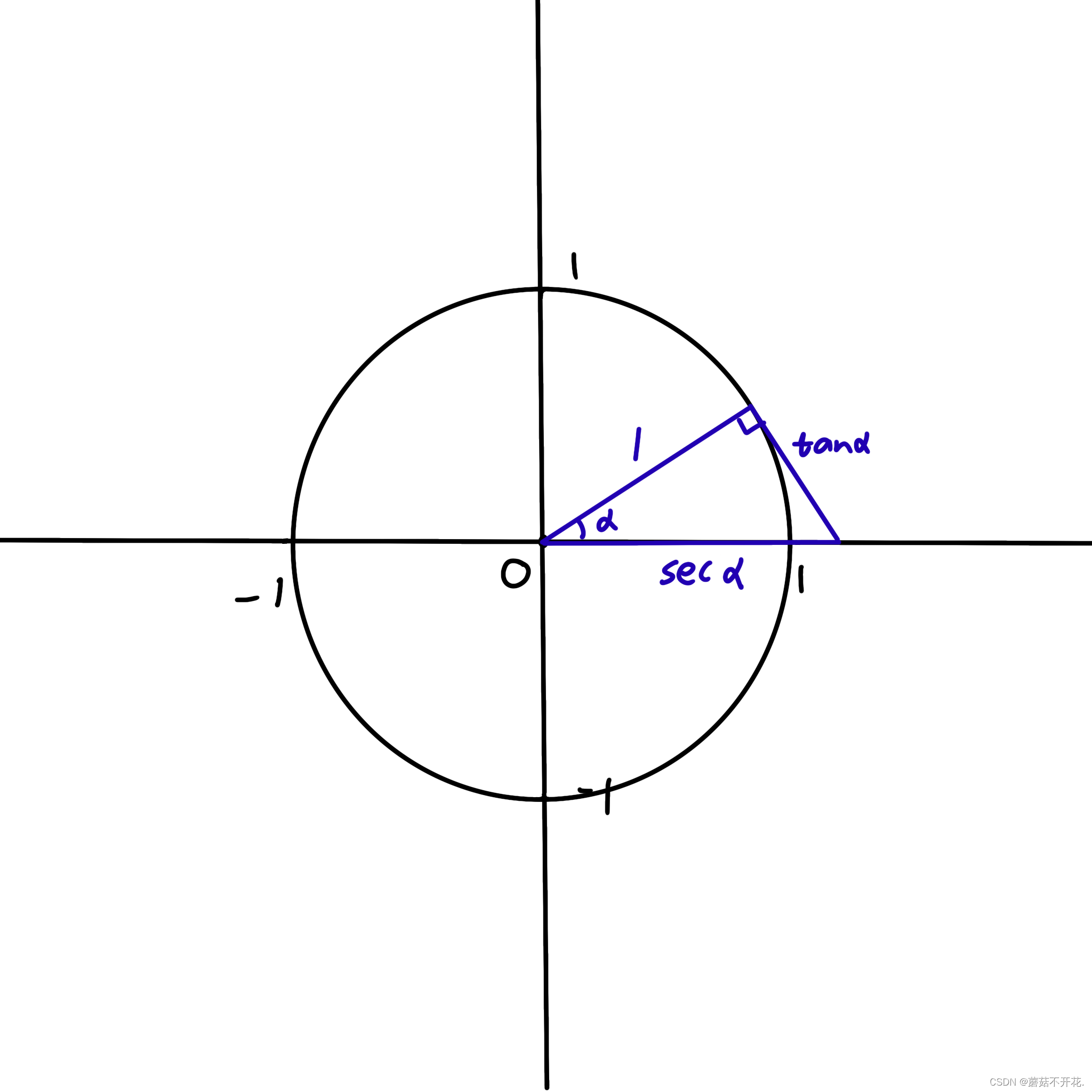
将x轴的单位“1”逆时针旋转α°,再从顶点向x轴作该线的垂线,就可以构造一个三角形,这个三角形的三条边分别是1,tanα,secα。
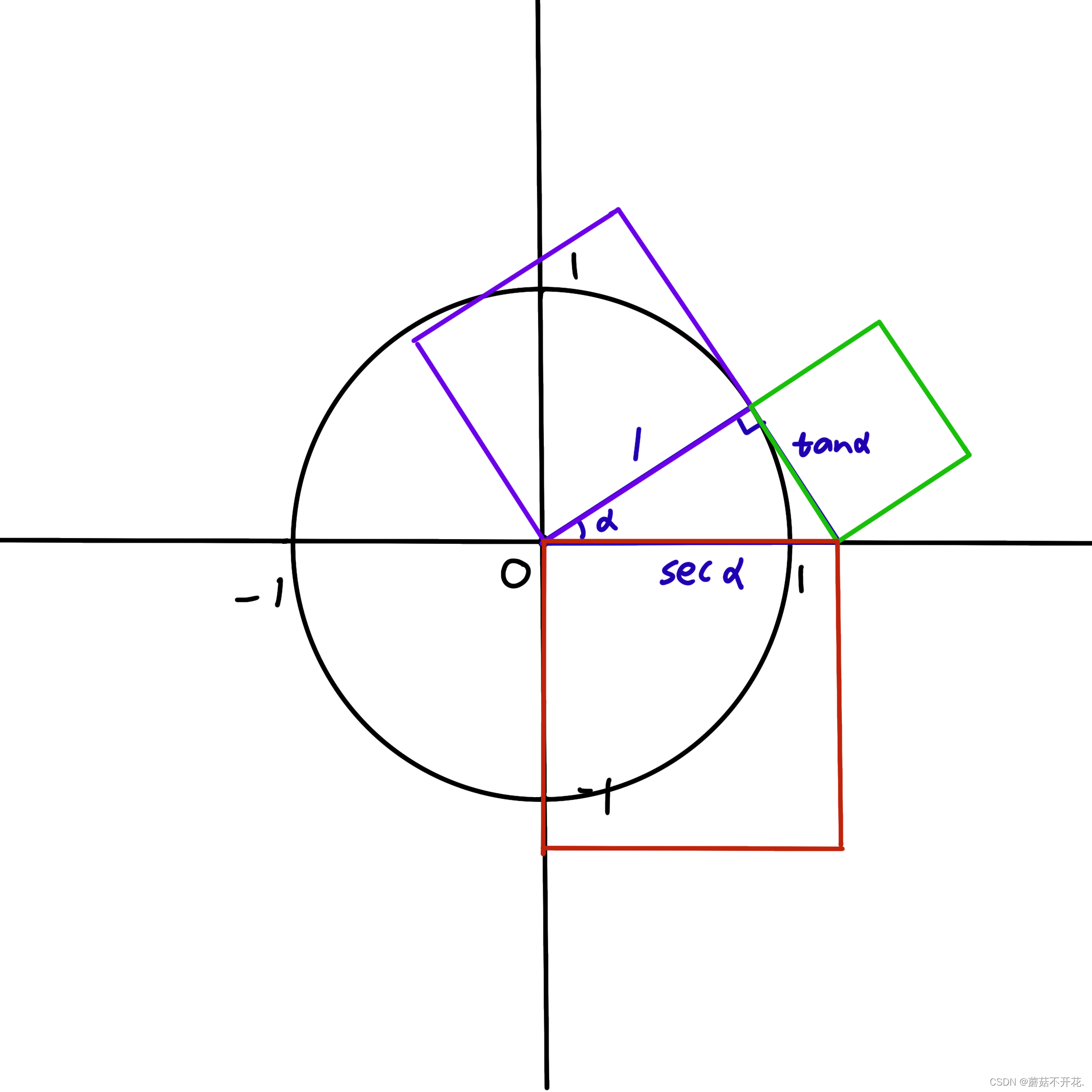
同理可得:tan²α+1=sec²α。
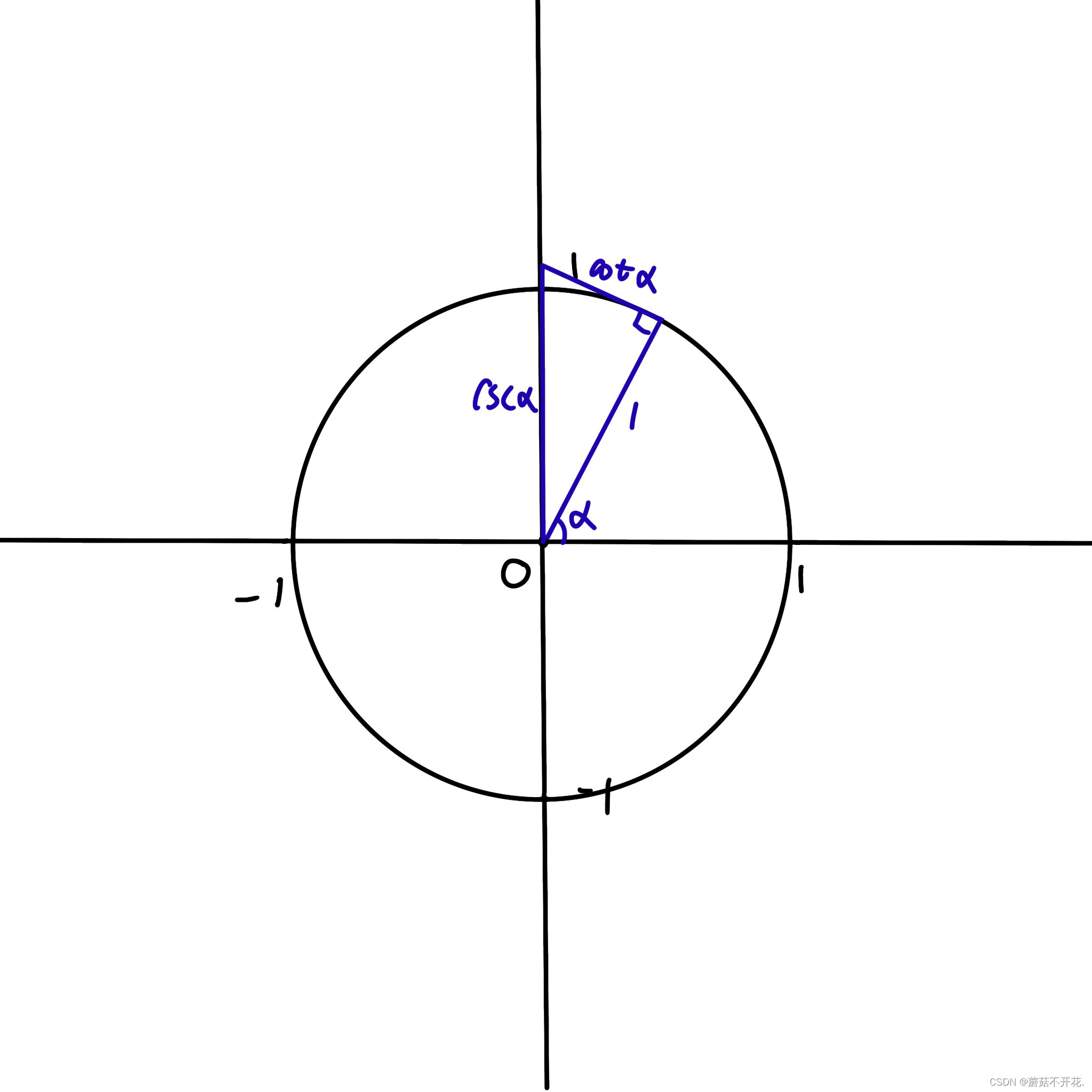
将x轴的单位“1”逆时针旋转α°,再从顶点向y轴作该线的垂线,就可以构造一个三角形,这个三角形的三条边分别是1,cotα,cscα。
同理可得:cot²α+1=csc²α。
立方数求和:
公式为
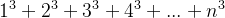
要求这个公式的解,我们可以先把立方数的图像画出来:
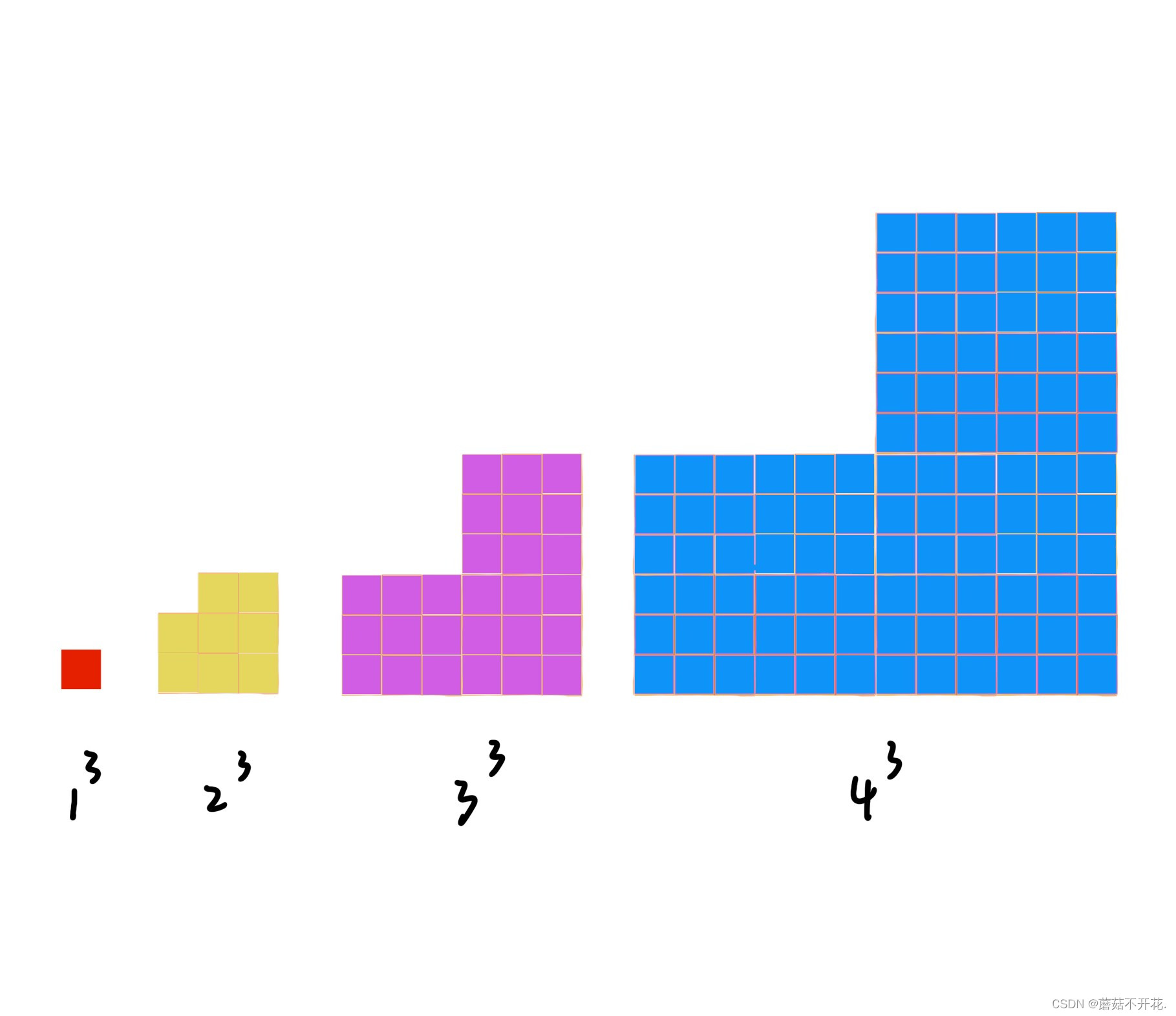
上图中分别是1,2,3,4的三次方,相信你们已经联想到这四个图形可以做什么了。
没错,让我们把它们拼起来~
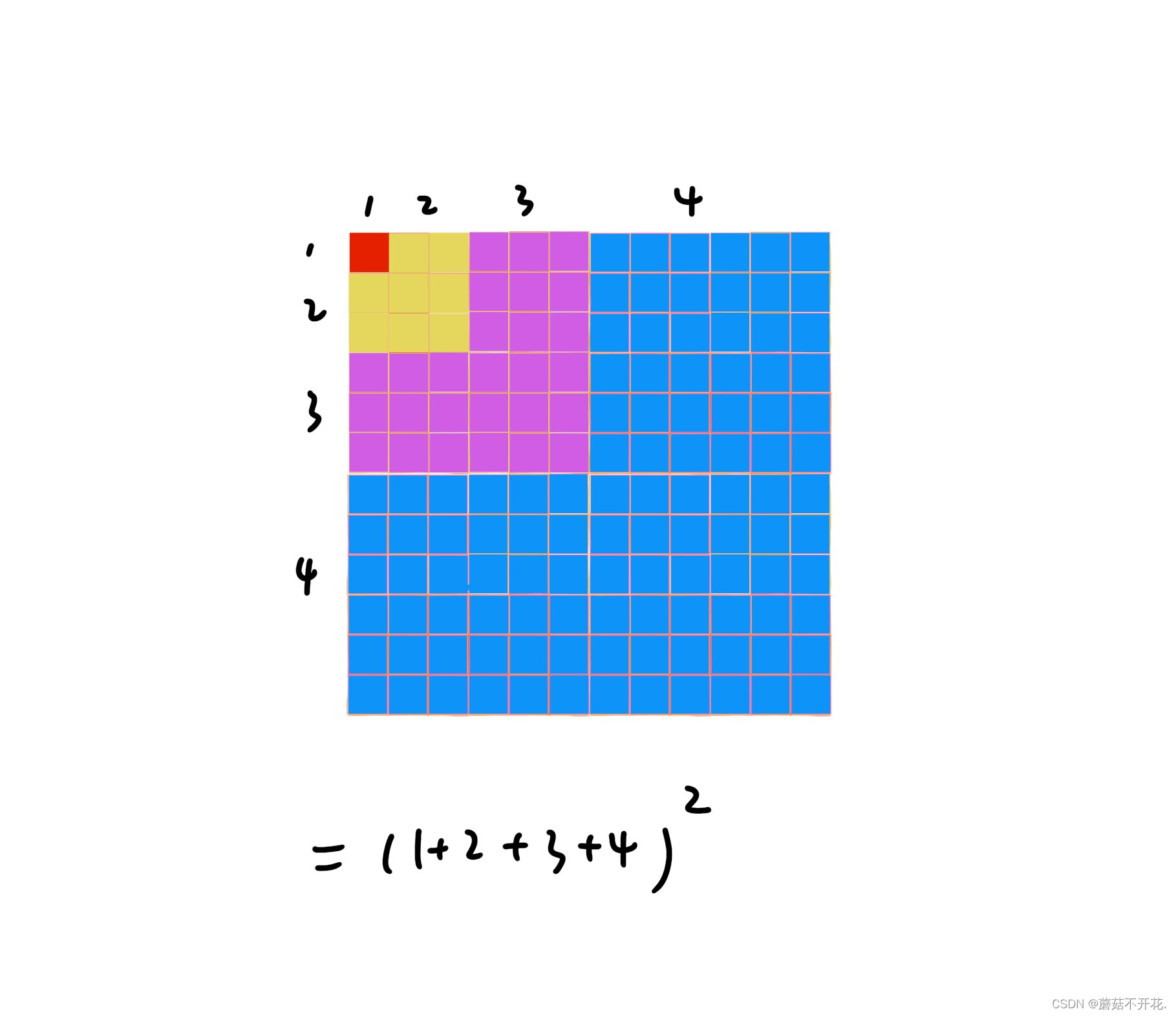
这四个数字的立方和竟然等于四个数字和的平方!
那么由这个规律 ,我们可以推出第一个公式的答案了:
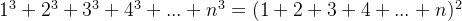
(a-b)²以及a²-b²的几何验证:
我们以前学习完全平方公式时,只知道公式的写法,但不知道它的几何意义,所以这次让我们用正方形的面积来研究一下:
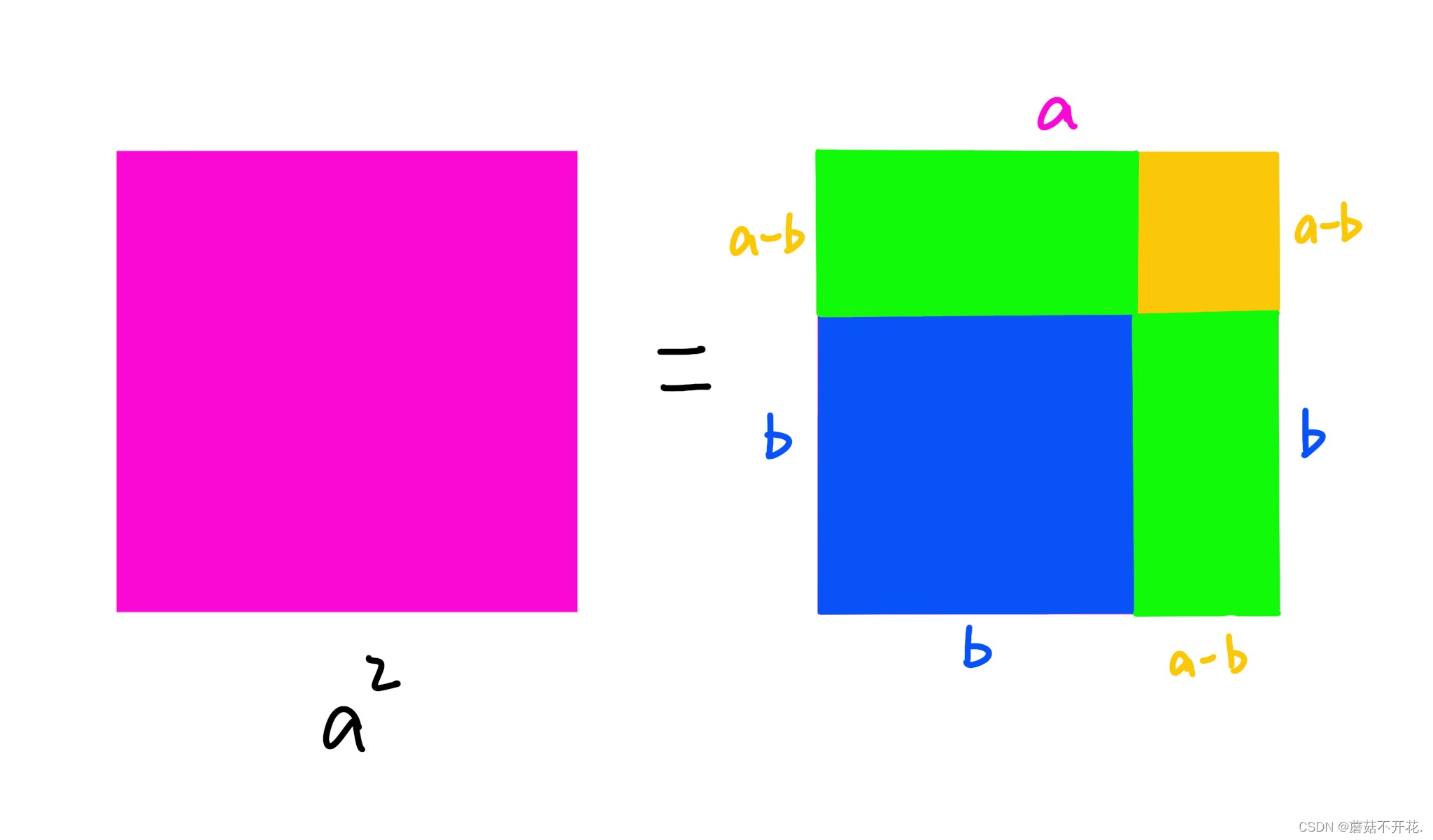
左图粉色的为面积为a²的正方形,接着我们在这个正方形中裁剪出一个蓝色的面积为b²的小正方形,再把剩下的部分用一条直线分成两部分,这样我们就可以得到一个公式:
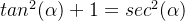 ;
;然后把(a-b)²单独移到一边,就可以推导出它的公式了:
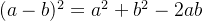 ;
;同理,a²-b²只需要将黄色和绿色块代表的面积相加:
奇数求和公式:
若要求1+3+5+7+9+...+2n-1的值,我们第一想到的应该是等差公式,然后可以求出它的答案,但若要根据它的几何意义来求值,可以怎么做?
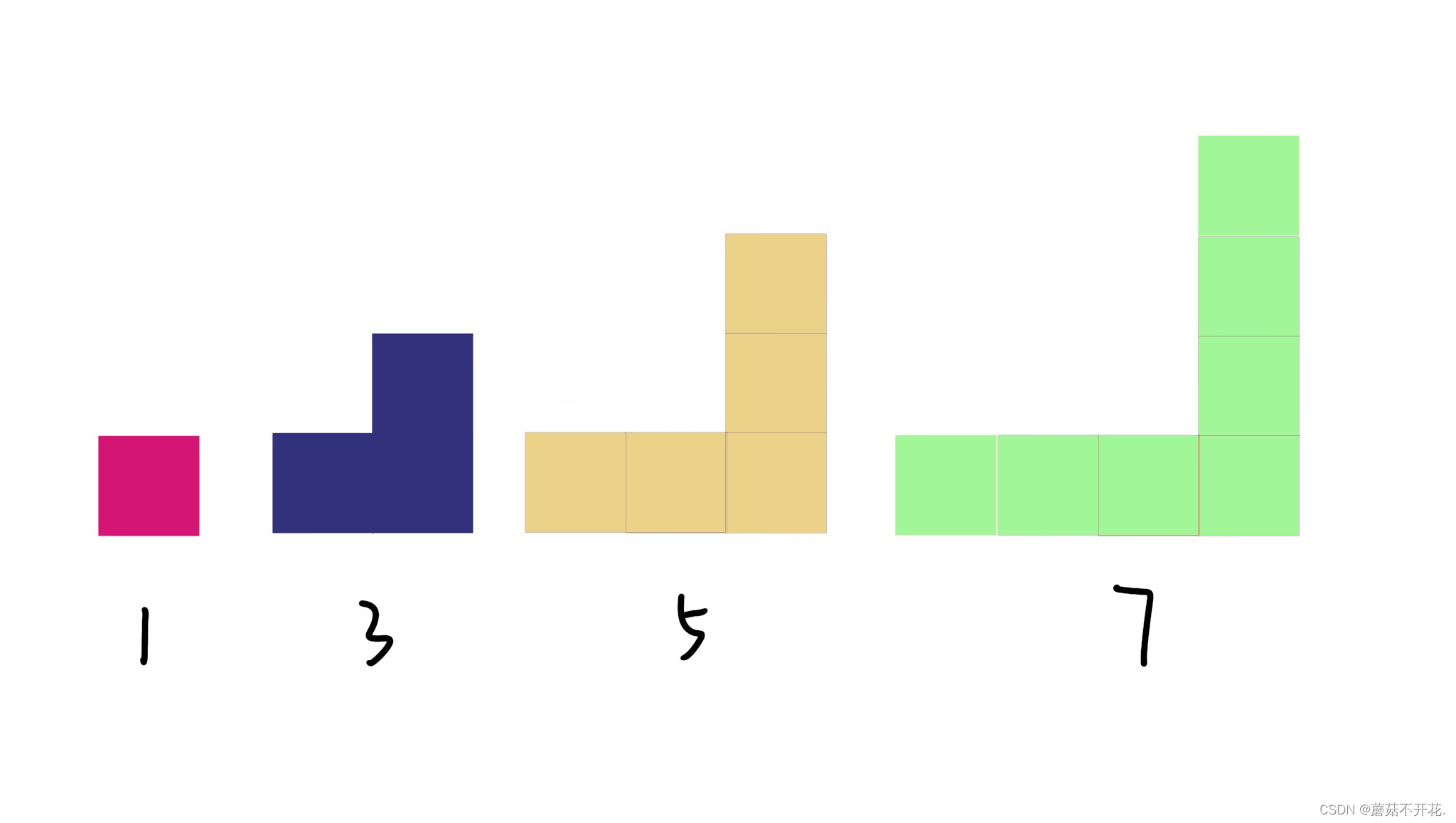
我们将公式中的各个奇数用方块的形式表示出来,摆出上图的形状,接着顺势将它们叠放起来:

观察一下它的边长,这是一个边长为4的正方形,也就是说 ,它包含了4²个方块。
根据这个规律,我们如果要求奇数的和,只需要知道式子里是几个奇数的和即可,若是n个,答案就是n²。(注:该式子必须为1开始,相邻奇数的和)
所以原式的值就是:
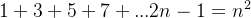
-
相关阅读:
指定端口被system程序占用解决方法
C语言 | Leetcode C语言题解之第141题环形链表
java基于springboot游乐场员工管理系统
C 语言获取文件绝对路径
SQL命令及MariaDB(一)
【毕业设计】基于stm32的智能扫地机器人设计与实现 - 单片机 物联网
nn.functional.sigmoid
java的入门学习
【UniApp】-uni-app-处理项目输入数据(苹果计算器)
单片机-控制按键点亮LED灯
- 原文地址:https://blog.csdn.net/weixin_72718640/article/details/133205967