【数据结构与算法】一文带你学透——算法分析

前言

  本期我们主要学习的是数据结构与算法中的如何分析代码的运行效率，以及对算法复杂度的定义。

目录

---

一、函数的渐进增长

   函数的渐近增长：给定两个函数 f(n)和 g(n)，如果存在一个整数 N，使得对于所

有的 n>N，f(n)总是比 g(n)大，那么，我们说 f(n)的增长渐近快于 g(n)。

  下面我们通过四个测试来说明函数的渐近增长

测试一

可以这样理解：

测试二 

 由函数图像我们可以得出与最高次相乘的常数不重要。当x无限大时,算法B1和算法B2几乎是重合的状态。

测试三

通过上述的函数图样，可以得出：最高次项的指数越大，函数的增长速度就越快。 

测试四

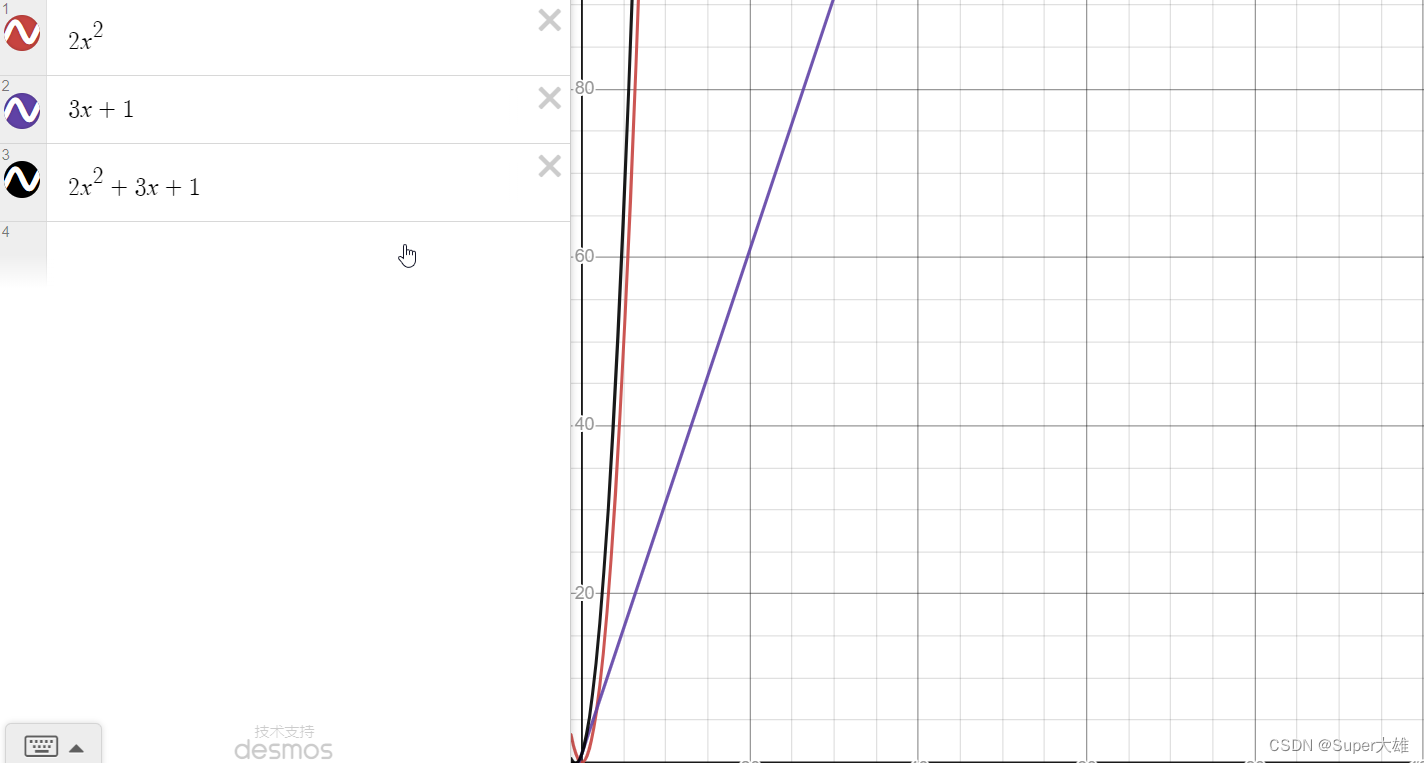
通过上述的函数图样，可以得出：判断一个算法的效率时，函数中的常数和其他次要项常常可以忽略，而更应该关注主项（最高项）的阶数。 

二 算法时间复杂度的定义

  大O记法定义 ：在进行算法分析时，语句总的执行次数 T(n) 是关于问题规模 n

的函数，算法的时间复杂度，就是算法的时间量度，记作 :T(n)=O(f(n)) ，其中 f(n)

是问题规模 n 的某个函数。用大写 O() 来体现算法时间复杂度的记法，我们称之

为 大O记法 。

2.1 大O阶的使用

如果T(n)=4n^3+3n^2+2n+1

(1)用常数1取代所有运行时间中的加法常数

T(n)=4n^3+3n^2+2n+1

(2)只保留最高阶

T(n)=4n^3

(3)如果最高阶存在且常数因子不为1则去除这个项相乘的常数

T(n)=n^3

2.2 常见的大O阶

2.2.1 线性阶

 一般含有非嵌套循环涉及线性阶，线性阶就是随着输入规模的扩大，对应计算次

数呈直线增长。

#include 
main(){
	int sum=0,n=100,i;
	for(i=1;i<=n;i++){
		sum+=i;
	}
}

2.2.2 平方阶

一般嵌套循环属于这种时间复杂度

#include 
main(){
	int sum=0,i,j,n=100;
	for(i=1;i<=n;i++){
		for(j=1;j<=n;j++){
			sum+=i*j;
		}
	}
}

2.2.3 立方阶

一般三层嵌套循环属于这种时间复杂度

#include 
main(){
	int sum=0,i,j,n=100,k;
	for(i=1;i<=n;i++){
		for(j=1;j<=n;j++){
			for(k=1;k<=n;k++)
			sum+=i*j;
		}
	}
}

2.2.4 对数阶

#include 
main(){
	int i=1;n=20;
	while(i
	i*=2;
}

    上面这段代码执行了2^x<=n次,大O阶为O(log2(n)); 

2.2.5 常数阶

一般不涉及循环操作的都是常数阶，因为它不会随着 n 的增长而增加操作次数。 

#include 
main(){
	int i=1;n=20;
	i+=n;
}

  上端代码不考虑n的规模，运行只执行两次，故使用O(1)来表示。

 2.3 常见的时间复杂度

 

2.4 最坏情况 

    从心理学角度讲，每个人对发生的事情都会有一个预期，比如打工人今天赚500money，有人会觉得赚了500money觉得开心，而有人会觉得才赚了500money。一般人在预期的时候趋向做最坏的打算，这样即使最糟糕的结果出现，当事人也有了心理准备，比较容易接受结果。假如最糟糕的结果并没有出现，当事人会很快乐。算法分析也是类似。

例如：我们从数组中找到一个指定的数值A

最好情况：开始遍历的时候第一个数就是数值A

最坏情况：表里到最后才找到数组中的数值A

平均情况：任何数字查询的平均成本是O(n/2)

      最坏情况是一种保证，在应用中，这是一种最基本的保障，即使在最坏情况下，

也能够正常提供服务，所以， 除非特别指定，我们提到的运行时间都指的是最坏

情况下的运行时间。

 三 函数的空间复杂度

      计算机的软硬件都经历了一个比较漫长的演变史，作为为运算提供环境的内存， 更是如此，从早些时候的 512k, 经历了 1M ， 2M ， 4M... 等，发展到现在的 8G ，甚至 16G 和 32G 。早期，算法在运行过程中对内存的占用情况也是一个经常需要考虑的问题，可以用算法的 空间复杂度 来描述算法对内存的占用。

     由于现在的计算机设备内存一般都比较大，基本上个人计算机都是 8G 起步，大的可以达到 128G，所以内存占用一般情况下并不是我们算法的瓶颈，普通情况下直接说复杂度，默认为算法的时间复杂度。

总结

  本期主要学习了函数的渐进式增长和时间复杂度大O阶的表示，大O阶是考试中特别容易出题的地方，希望大家好好看看！

---