-
支持向量机(SVM)案例分析
支持向量机(support vector machines, SVM)是一种二分类模型,所谓二分类模型是指比如有很多特征(自变量X)对另外一个标签项(因变量Y)的分类作用关系,比如当前有很多特征,包括身高、年龄、学历、收入、教育年限等共5项,因变量为‘是否吸烟’,‘是否吸烟’仅包括两项,吸烟和不吸烟。那么该5个特征项对于‘是否吸烟’的分类情况的作用关系研究,则称为‘二分类模型’,但事实上很多时候标签项(因变量Y)有很多个类别,比如某个标签项Y为‘菜系偏好’,中国菜系有很多,包括川菜、鲁菜、粤菜、闽菜、苏菜、浙菜、湘菜和徽菜共计8类,此时则需要进行‘多分类决策函数’转化,简单理解为两两类别(8个中任意选择2)分别建立SVM模型,然后进行组合使用。
机器学习算法常见算法中包括决策树、随机森林、贝叶斯等,上述均有良好的可解释性,比如决策树是将特征按分割点不停地划分出类别,随机森林是多个决策树模型,贝叶斯模型是利用贝叶斯概率原理进行计算。与上述不同,支持向量机模型是利用运筹规划约束求最优解,而此最优解是一个空间平面,此空间平面可以结合特征项,将‘吸烟’和‘不吸烟’两类完全地分开,寻找该空间平面即是支持向量机的核心算法原理。
支持向量机的计算原理复杂,但对其通俗地理解并不复杂,只需要知道其需要求解出‘空间平面’,该‘空间平面’可以把不同的标签项(因变量Y)类别特别明显的划分开即可。类似其它机器学习算法,支持向量机的构建步骤上,一般也需要先对数据进行量纲化处理、设置训练数据和测试数据比例、设置相关参数调优,最终实现在训练数据上有着良好表现,并且测试数据上也有着良好表现即可。
支持向量机模型案例
1 背景
本部分支持向量机使用的‘鸢尾花分类数据集’进行案例演示,其共为150个样本,包括4个特征属性(4个自变量X),以及标签(因变量Y)为鸢尾花卉类别,共包括3个类别分别是刚毛鸢尾花、变色鸢尾花和弗吉尼亚鸢尾花(下称A、B、C三类)。
2 理论
支持向量机模型的原理上,其可见下图。
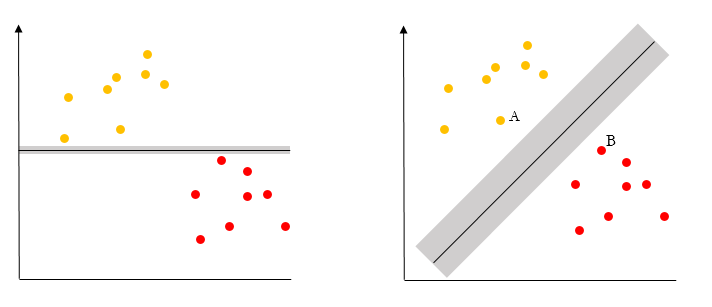
比如红色表示“吸烟”,黄色表示“不吸烟”,那么如何找到一个平面最大化的将两类群体分开,如上图所示,分开有很多种方式,左侧也可以分开,右侧也能分开。但明显的,右侧会“分的更开”,因而如何寻找到这样的一个空间平面,让标签项各类别最为明显的分开,此算法过程即为支持向量机。将点分开时,离平面最近的点要尽可能的远,比如右侧时A点和B点离平面最近,那么算法需要想办法让该类点尽可能地远离平面,这样就称为“分的更好”。左侧时挨着平面最近的两个点离平面太近,所以右侧的分类更好。
与此同时,理论上可以找到‘空间平面’,将点彻底完全地分开,但此种情况并没有用,因为它只是数学上彻底地分开,但对真实数据业务并没有帮助,与此同时,数学计算上如果尽可能地让点分开,那么很容易出现‘过拟合’现象,即训练数据时模型构建完美,但测试数据上的表现糟糕,因而通过可对此类情况进行惩罚,即设置‘误差项惩罚系数值’。另外,为构建出空间平面,还需要使用到非线性函数,SVM模型时称‘核函数’,其用用于将特征从低维(比如二维XY轴平面)向高维空间转换,并且对其进行一定参数设置,以寻找较优模型。
结合支持向量机的原理情况,其涉及以下参数,如下:

上述参数中,误差项惩罚系数是一个惩罚值,该值越大时训练数据越容易表现良好,但越容易产生‘过拟合’现象。参数调整时,如果发现有‘过拟合’情况,建议将该值往下设置,SPSSAU默认该值为1(已经较小)。核函数是SVM算法时,将低维向高维转化的‘助手’,建议设置方式如下:

核函数系数值(也称Gamma值),其意义相对较小,通常使用默认值即可;
核函数最高次幂:如果使用多项式核函数时,最高次幂越大,模型效果越好,但更容易带来‘过拟合’问题,建议设置为2、3或者4进行对比比(默认该值为3);
多分类决策函数:基础的的SVM只处理二分类问题,如果标签项(因变量Y)有多个类别,比如8大菜系共8个类别时,那么算法上有两种方式,第1种是每个类别与余下类别(作为反例)建立1个SVM然后整合(共计建立8个SVM),即ovr法(1对其余法),还有一种方式是两两配对法即ovo法,8个类别形成8*(8-1)/2=28个配对组合,即进行28次SVM然后整合,该项默认值为ovr法。
最后:模型收敛参数值和最大迭代次数这两项,其为算法内部迭代求最优解的参数值,正常情况下不用设置。
3 操作
本例子操作如下:

训练集比例默认选择为:0.8即80%(150*0.8=120个样本)进行训练支持向量机模型,余下20%即30个样本(测试数据)用于模型的验证。需要注意的是SVM时涉及距离计算,因而需要对特征进行量纲处理,通常量纲处理方式为正态标准化,此处理目的是让数据保持一致性量纲。当然也可使用其它的量纲方式,比如区间化,归一化等。
接着对参数设置如下:

误差项惩罚系数值为1,如果希望训练集数据有着更好的表现,则可将其设置更高,但一定需要注意此时测试集的效果情况,否则就会出现‘过拟合’现象。本案例数据仅4个特征X,训练数据量为120个,因而使用高斯核较为适合,核函数系数值默认。多分类决策函数上使用ovr(即一对多余法),这样会减少运行时间加快运行速度。模型收敛参数和最大迭代次数保持默认值。
4 SPSSAU输出结果
SPSSAU共输出5项结果,依次为基本信息汇总,训练集或测试集模型评估结果,测试集结果混淆矩阵,模型汇总表和模型代码,如下说明:

上述表格中,基本信息汇总展示出因变量Y(标签项)的分类分布情况,模型评估结果(包括训练集或测试集)用于模型的拟合效果判断,尤其是测试集的拟合效果,以及提供测试集数据的混淆矩阵结果;模型汇总表格将各类参数值进行汇总,并且在最后附录SVM模型构建的核心代码。
5文字分析
接下来针对最重要的模型拟合情况进行说明,如下表格:

上表格中分别针对训练集和测试集,提供四个评估指标,分别是精确率、召回率、f1-scrore、准确率,以及平均指标和样本量指标等,如下表格说明:

具体上述具体指标的解读,可见决策树模型帮助手册,通常使用F1-score值进行评估即可,训练数据时f1-score值为0.96,并且测试集数据也保持着0.94高分,二者比较接近,因而意味着应该不存在‘过拟合’现象,而且模型良好。
接着进一步查看测试数据的‘混淆矩阵’,即模型预测和事实情况的交叉集合,如下图:

‘混淆矩阵’时,右下三角对角线的值越大越好,其表示预测值和真实值完全一致。上图中仅B类中2个样本被判断成C类,其余全部正确,意味着本次支持向量机模型在测试数据上表现良好。最后SPSSAU输出模型参数信息值,如下表格:

上述参数信息仅为再次输出汇总,并无其它目的,最后SPSSAU输出使用python中slearn包构建本次支持向量机模型的核心代码如下:
model = svm.SVC(C=1.0, kernel=rbf, gamma=scale, tol = 0.001, max_iter=2000, decision_function_shape=ovr)
model.fit(x_train, y_train)
6 剖析
涉及以下几个关键点,分别如下:
- 支持向量机模型时是否需要标准化处理?
一般建议是进行标准化处理,因为SVM模型时涉及距离计算,需要量纲化数据处理,通常使用正态标准化处理方式即可。 - 保存预测值
保存预测值时,SPSSAU会新生成一个标题用于存储模型预测的类别信息,其数字的意义与模型中标签项(因变量Y)的数字保持一致意义。 - SPSSAU进行支持向量机模型构建时,自变量X(特征项)中包括定类数据如何处理?
支持向量机模型时本身并不单独针对定类数据处理,如果有定类数据,建议对其哑变量处理后放入,关于哑变量可点击查看。
http://spssau.com/front/spssau/helps/otherdocuments/dummy.html - SPSSAU中随机模型合格的判断标准是什么?
机器学习模型中,通常均为先使用训练数据训练模型,然后使用测试数据测试模型效果。通常判断标准为训练模型具有良好的拟合效果,同时测试模型也有良好的拟合效果。机器学习模型中很容易出现‘过拟合’现象即假的好结果,因而一定需要重点关注测试数据的拟合效果。针对单一模型,可通过变换参数调优,与此同时,可使用多种机器学习模型,比如使用决策树、随机森林、神经网络等,综合对比选择最优模型。 - 支持向量机SVM更多参考资料?
更多关于SVM的资料,可通过sklearn官方手册查看,点击查看。
https://scikit-learn.org/stable/modules/svm.html#svm-classification - SPSSAU进行SVM支持向量机时提示数据质量异常?
当前SVM支持分类任务,需要确保标签项(因变量Y)为定类数据,如果为定量连续数据,也或者样本量较少(或者非会员仅分析前100个样本)时可能出现无法计算因而提示数据质量异常。
- 支持向量机模型时是否需要标准化处理?
-
相关阅读:
python如何不生成pyc文件(三种方式)
【The design pattern of Attribute-Based Dynamic Routing Pattern (ADRP)】
.NET 7 发布的最后一个预览版Preview 7, 下个月发布RC
【OpenCV • c++】图像噪音 | 椒盐噪音 | 高斯噪音
Day18_VueComponent
Android 开源一个USB读写demo,从多个USB设备中选择一个实现外设控制的通信
Day20 | 每天五道题
Java 设计模式 — 抽象工厂模式(2)
Python程序龟速过载怎么办,asyncio并发教程来解决
看了我的mybatis-plus用法,同事也开始悄悄模仿了
- 原文地址:https://blog.csdn.net/m0_37228052/article/details/132986762