E. Round Dance

Problem - 1833E - Codeforces

题意：n个点，每个顶点有两条边使其全是环。现在只知道一个顶点相邻的一个顶点，求可以形成的最少的环和形成最多的环数量。

思路：可以知道最多环数量就是连通块数，因为题目给的就一定保证了存在不会有单点。最少的一定是将链连成一个环。怎么找环呢，最开始是写了个基环树，发现两个点的环需要特判，可能还有其他情况。

1连2，2连1。这种情况可以发现它既可以是环也可以是链。因为1的一个相邻点被连了，2的一个相邻点被连了，但是1和2都还有另一个点没有被连上。这个时候用基环树判断是环后还要根据环内点数进行再次判断。

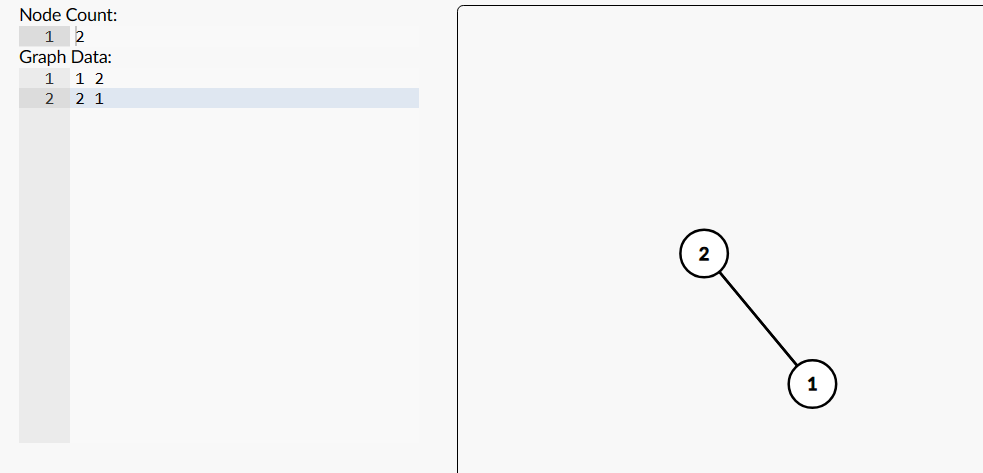
在用基环树没过样例发现了上面那个特殊环之后，又仔细读了读这题题面。发现它除了2个点的环特殊外，其他的一定要么是环要么是链，不会有其他的。

像下面这个图，题目要求一定是成环的且没有其他杂边，但是这个有一个咋边，经过手推发现这个是不合法的。

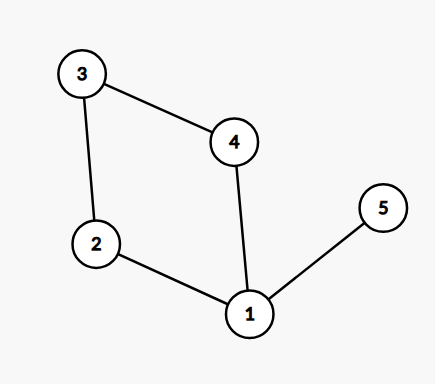
这个也是不合法的。

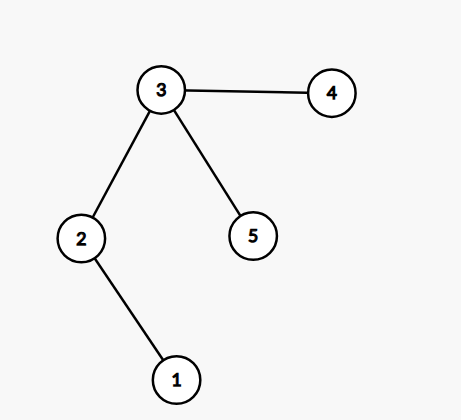
进一步发现，似乎不用基环树找环这么麻烦。建双边，对边去重，度为1的一定可以是链，度为2的一定是环。并且不会出现一个环内既有度为1的，也有度为2的这种情况。

综上：用并查集找连通块个数，之后找到链的个数即可。

void solve() {
    int n; cin>>n;
    vector<int> p(n + 1), ins(n + 1);
    // 因为建树，又不遍历，还要去重，不如用set存储。
    vector<set<int>> g(n + 1);
    iota(all(p), 0);
    auto find = [&](auto &&self, int x) -> int {
        return p[x] == x ? x : p[x] = self(self,p[x]);
    };
    auto merge = [&](int u, int v) -> void {
        int fu = find(find,u), fv = find(find,v);
        if(fu != fv) {
            p[fu] = fv;
        }
    };
    for(int i = 1; i <= n; ++i) {
        int t; cin>>t;
        merge(t,i);
        g[i].insert(t);
        g[t].insert(i);
    }
    for(int i = 1; i <= n; ++i) {
        // 度为1的一定是可以是链（**可以**，环内点数为的特殊，既是环，又是链
        ins[find(find,i)] |= g[i].size() == 1;
    }
    int cnt = 0, chain = 0;
    for(int i = 1; i <= n; ++i) {
        if(find(find,i) == i) {
            cnt++;
            chain += ins[i];
        }
    }
    // 取最小的，可能没有链，就多加了一个了
    cout<<min(cnt, cnt - chain + 1)<<" "<<cnt<<endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

用基环树写的也调出来了。

找到环后，再判断是否是长度为2的环就行，长度为2的环可以当作链。

Codeforces Round 874 (Div. 3) A~G - 知乎 (zhihu.com)

Graph Editor (csacademy.com)