并查集 size 的优化

我们把如下图所示的并查集，进行 union(4,9) 操作。

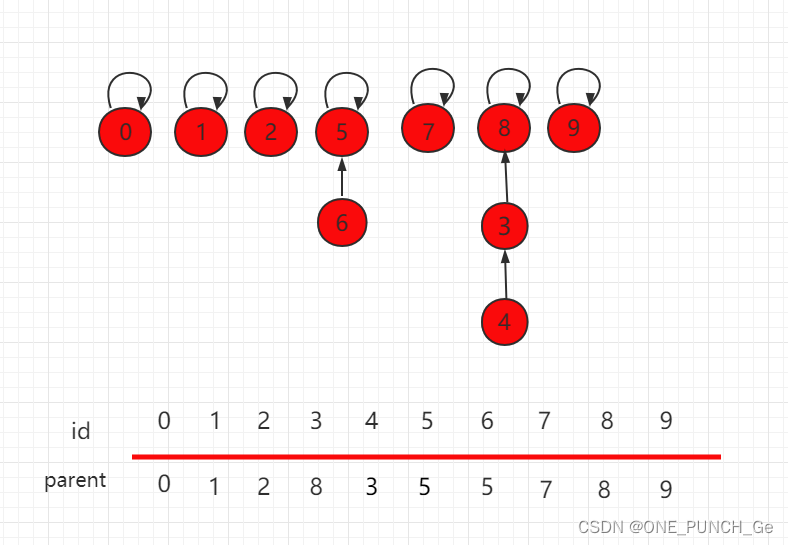
合并操作后的结构为：

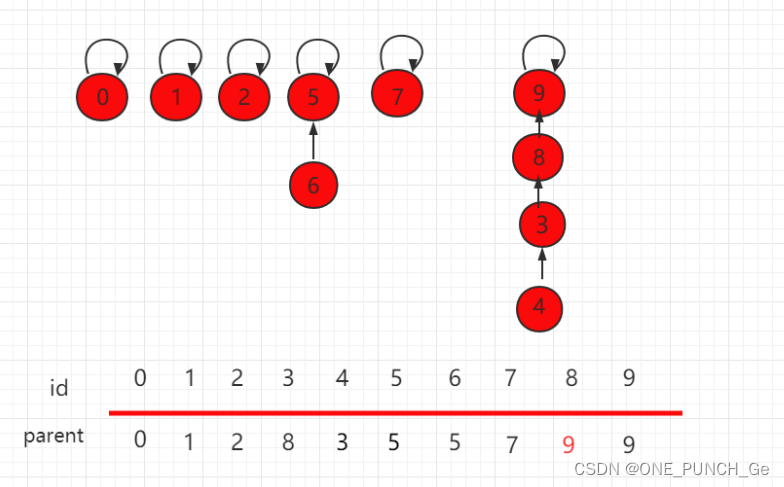
可以发现，这个结构的树的层相对较高，若此时元素数量增多，这样产生的消耗就会相对较大。解决这个问题其实很简单，在进行具体指向操作的时候先进行判断，把元素少的集合根节点指向元素多的根节点，能更高概率的生成一个层数比较低的树。

构造并查集的时候需要多一个参数，sz 数组，sz[i] 表示以 i 为根的集合中元素个数。

// 构造函数
public UnionFind3(int count){
    parent = new int[count];
    sz = new int[count];
    this.count = count;
    // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
    for( int i = 0 ; i < count ; i ++ ){
        parent[i] = i;
        sz[i] = 1;
    }
}

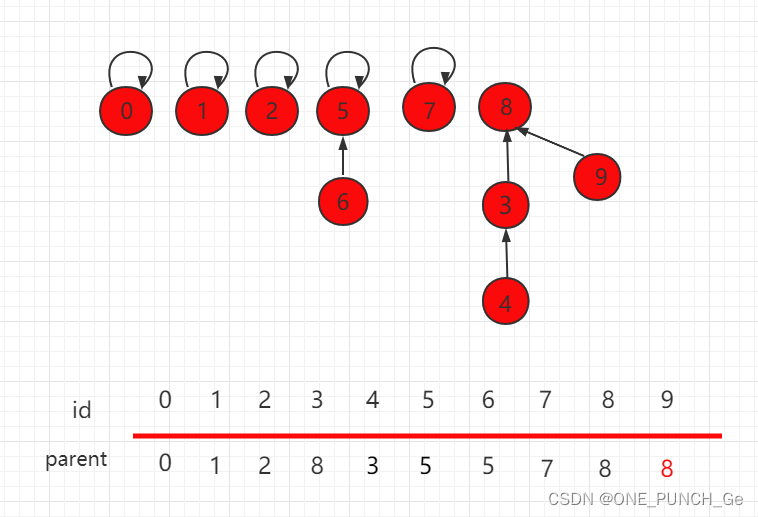
在进行合并操作时候，根据两个元素所在树的元素个数不同判断合并方向。

public void unionElements(int p, int q){
    int pRoot = find(p);
    int qRoot = find(q);
    if( pRoot == qRoot )
        return;
    if( sz[pRoot] < sz[qRoot] ){
        parent[pRoot] = qRoot;
        sz[qRoot] += sz[pRoot];
    }
    else{
        parent[qRoot] = pRoot;
        sz[pRoot] += sz[qRoot];
    }
}

优化后，合并结果如下，9 指向父节点 8。

Java 实例代码

UnionFind3.java 文件代码：

package runoob.union;
 
/**
 * 并查集size的优化
 */
public class UnionFind3 {
    // parent[i]表示第一个元素所指向的父节点
    private int[] parent;
    // sz[i]表示以i为根的集合中元素个数
    private int[] sz;
    // 数据个数
    private int count;
 
    // 构造函数
    public UnionFind3(int count){
        parent = new int[count];
        sz = new int[count];
        this.count = count;
        // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
        for( int i = 0 ; i < count ; i ++ ){
            parent[i] = i;
            sz[i] = 1;
        }
    }
 
    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    private int find(int p){
        assert( p >= 0 && p < count );
        // 不断去查询自己的父亲节点, 直到到达根节点
        // 根节点的特点: parent[p] == p
        while( p != parent[p] )
            p = parent[p];
        return p;
    }
 
    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    public boolean isConnected( int p , int q ){
        return find(p) == find(q);
    }
 
    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    public void unionElements(int p, int q){
        int pRoot = find(p);
        int qRoot = find(q);
        if( pRoot == qRoot )
            return;
        // 根据两个元素所在树的元素个数不同判断合并方向
        // 将元素个数少的集合合并到元素个数多的集合上
        if( sz[pRoot] < sz[qRoot] ){
            parent[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        }
        else{
            parent[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }
    }
}