基础算法---离散化

概念

离散化，把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。

通俗的说，离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小。

也就是说当数据空间跨越太大,但是数据的个数却不多,我们可以使用离散化将许多无意义的操作去掉

例如 数组的长度是10^9 但是只有100000个下标上的值不为0 ,当我们需要求某个区间[l,r]内的和 ,如果不离散化,就要从l开始遍历到r,才可以求出区间和,如果l和r相差很大,就会浪费很多时间,其中很多值为0,所以我们加了很多无意义的数

离散化

有一组数据 {1,5000,60,99999,88,88}存到一个数组里后 ,先排序 ---> {1,60,88,88,5000,99999} 去重 --->{1,60,88,5000,99999} ,二分查找得到下标 {1,2,3,4,5}

为什么要排序? 为了等下查找数据的时候可以使用二分查找,例如查找60这个数字

为什么要去重? 要确保相同元素离散化的结果相同

看个题目

假定有一个无限长的数轴，数轴上每个坐标上的数都是 0 。

现在，我们首先进行 n 次操作，每次操作将某一位置 x 上的数加 c 。

接下来，进行 m 次询问，每个询问包含两个整数 l 和 r，你需要求出在区间 [l,r] 之间的所有数的和。

输入格式

第一行包含两个整数 n 和 m。

接下来 n 行，每行包含两个整数 x 和 c。

再接下来 m 行，每行包含两个整数 l 和 r 。

输出格式

共 m 行，每行输出一个询问中所求的区间内数字和。

数据范围

−10 ^9 ≤x≤ 10 ^9,

1≤n,m≤10^5,

−10^ 9 ≤l≤r≤ 10 ^9,

−10000≤c≤10000

输入样例：

3 3
1 2
3 6
7 5
1 3
4 6
7 8

输出样例：

8
0
5

#include <iostream>
#include <vector>
 
#include <algorithm> //sort函数的头文件
using namespace std;
 
const int N = 300010;
int a[N], s[N];
 
typedef pair<int, int>  PII;
 
vector <int> alls; // 存储着 x l r
vector <PII> insert; // 存储操作坐标x和增量c
vector <PII> inquiry; // 存储着询问区间 l 和 r
 
int find(int x) //二分查找: 找x l r 离散后的坐标
{
	int l = 0, r = alls.size() - 1;
	while (l < r)
	{
		int mid = l + r >> 1;
		if (alls[mid] >= x)
		{
			r = mid;
		}
		else
		{
			l = mid + 1;
		}
	}
	return r + 1; // 坐标是从1开始的
}
int main(void)
{
	int n, m;
	cin >> n >> m;
	while (n--)
	{
		int x, c;
		cin >> x >> c;
		alls.push_back(x);
		insert.push_back({ x,c });
	}
 
	while (m--)
	{
		int l, r;
		cin >> l >> r;
		alls.push_back(l);
		alls.push_back(r);
		inquiry.push_back({ l,r });
	}
 
	//排序alls数组排的是l、r、x的顺序，再去重，去的也是l、r、x的重复数字
	sort(alls.begin(), alls.end()); 
	// unique函数是将重复的元素放到数组的后边(并未删去) 
	// 返回值是第一个重复元素的下标
	//erase函数删除区间的元素
	alls.erase(unique(alls.begin(), alls.end()), alls.end());
 
	/*for (auto item:vec)不改变迭代对象的值,效果是利用item遍历并获得vec容器中的每一个值*/
	for (auto item : insert)
	{
		int x = find(item.first);
		a[x] += item.second;
	}
	
	for (int i = 1; i <= alls.size(); i++)
	{
		s[i] = s[i - 1] + a[i]; //求a[i]前缀和
	}
 
	for (auto item : inquiry)
	{
		int l = find(item.first), r =find( item.second);
		printf("%d\n", s[r] - s[l - 1]);
	}
 
	return 0;
}

讲解

根据输入样例,原数据应该是这样的

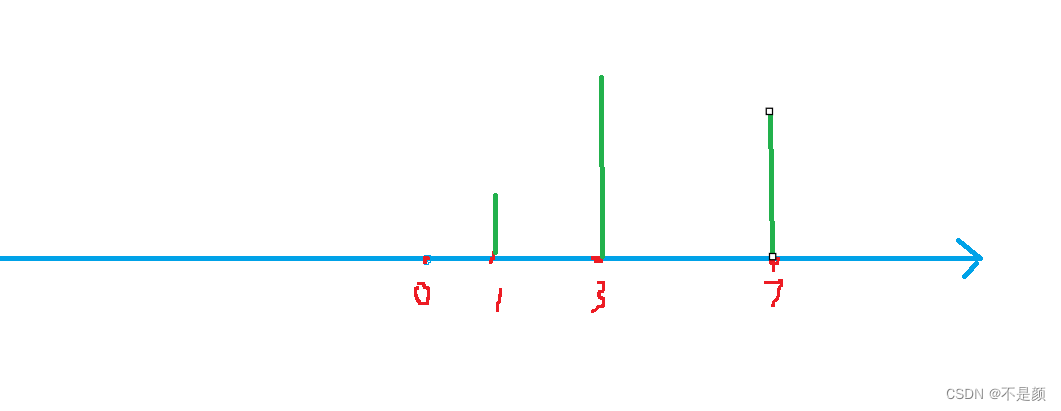
将x l r 存入alls--->alls  1 3 7 1 3 4 6 7 8

排序去重 --> alls  1 3 4 6 7 8

--------------------------------------------------------------------------------------

然后intsert 数组存储着操作下标和加数    { 1 , 2 } { 3 , 6 } { 7, 5 }

inquiry数组存储着询问区间     { 1, 3 }  { 4 , 6 }  { 7 , 8 }

--------------------------------------------------------------------------------------

然后我们有一个a数组,我们利用二分查找找得 1   3   7 对应的下标为  1 2 5 ,在这些位置增加 2 6 5 ,那么就得到了a数组 

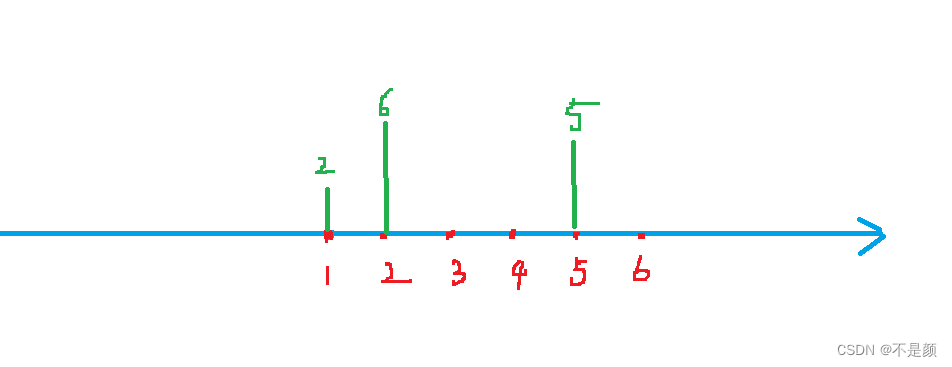
再把 区间 1 3 4 6 7 8利用二分得到离散化的坐标为  1 2 3 4 5 6

也就是说求[ 1 , 3 ]区间的和 就是求a数组 [ 1 ,  2 ] 区间的和 ... ...

到此得到答案