AVL树的实现

1.概念：

高度平衡二叉搜索树

这就是对应AVL树

其实现实在搜索二叉树的基础之上的：

主要步骤是通过平衡因子来确定是否满足AVL树的条件：

代码主要实现如下：

1.插入元素：

这里的插入元素与搜索二叉树的插入完全相同的。

2.通过平衡因子进行修改二叉搜索树，使其成为平衡二叉搜索树

具体分为6种情况：

1.新增的节点在左边，对应parent的平衡因子--

2.新增的节点在右边，对应parent的平衡因子++

3.更新后平衡因子==0，说明parent所在的子树高度不变，不会影响祖先，所以不用沿着root路径继续向上更新了，直接跳出循环并结束

4.更新后平衡因子==1 or -1，说明parent所在的子树高度变化，会影响祖先，所以需要沿着root1路径继续向上更新，循环继续

5.更新后平衡因子==2 or -2，说明parent所在的子树高度变化且不平衡，对parent所在的子树进行旋转，使其平衡，平衡之后自然退出循环。

6.如果一直更新到了根节点，也要直接跳出循环。

对应的代码如下：

对应旋转的代码分为左旋和右旋

左旋：说明parent的右子树和左子树的高度差等于2

所以要右子树的一部分子树向左旋转，即左旋：

图示如下：

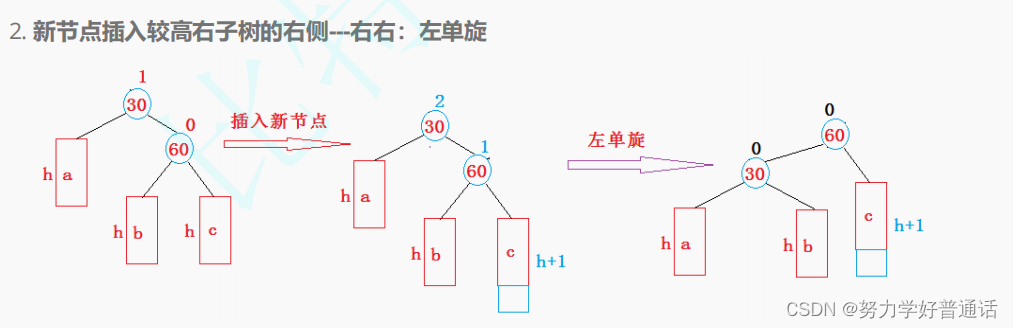
左旋的核心步骤有两个：

1.parent->_right= cur->_left

2.cur->left = parent

这是主要的核心步骤，但还有很多的细节需要大量代码完成

例如更新节点的父亲等等

代码如下：

右旋：

说明parent的左子树和右子树的高度差等于2

所以要左子树的一部分子树向右旋转，即右旋：

图示如下：

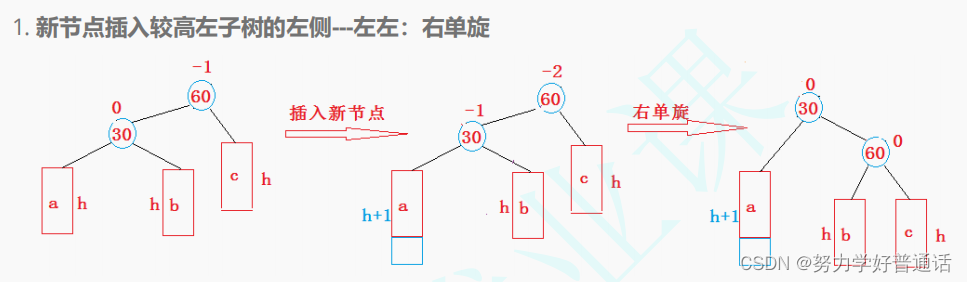
右旋的核心步骤有两个：

1.parent->_left = cur->_right

2.cur->_right = parent;

代码如下：

除了上述的两种情况外，还有两种更复杂的情况：

图示如下：

1.第一种情况：

对应的parent == 2,cur == -1

这种情况需要两次旋转：

第一次以90为parent进行一次右旋，第二次以30位parent进行一次左旋

可以理解为第一次只是预处理，将其变成parent == 2,cur == 1的情况

然后再用左旋即可。

对应的代码如下：

2.第二种情况：

图示：

对应的parent == -2,cur == 1

这种情况需要两次旋转：

第一次以30为parent进行一次左旋，第二次以90位parent进行一次右旋

可以理解为第一次只是预处理，将其变成parent == -2,cur == -1的情况

然后再用右旋即可。

代码如下：