数据结构算法-分而治之算法

引言

在茫茫人海中找寻那个特定的身影，犹如在浩瀚的星海中寻找那一颗独特的星辰。小森，一个平凡而真实的男孩，此时正在人群中寻找他的朋友，温迪。

小森运用了一种“分而治之”的算法策略，将周围的人群分成两组，一组在左边，一组在右边。他选择了一个方向，开始在他的部分寻找。

他按照人群的身高、发型、服装等特征将他们进行分类。他一边走，一边观察，一边思考。他的心跳在不断地提醒他，时间在流逝。

具体来说，小森的算法步骤如下：

将人群分为两组，分别在左右两边进行搜索。
对每一组人群，根据他们的身高、发型、服装等特征进行分类。
在每一类人群中，再次运用“分而治之”的策略，将他们分为更小的组别。
继续对每一类组别进行分类，直到找到温迪或排除该类人群。
他不断缩小搜索范围，将注意力集中在那些与温迪相似的人群上。他观察他们的行为、语言和姿态，试图从中发现温迪的影子。

他的心跳加速，他的手心出汗，他的眼睛在人群中焦急地扫视着。每一次的失望都像是一把尖锐的刀，刺入他的心中。

然而，他并没有放弃。他坚信，只有通过这种细致的搜索和耐心的等待，才能找到他想找的人。

突然，他看到了一个熟悉的身影。那个熟悉的笑容，那个熟悉的眼神，是温迪！他的心中充满了激动，他跑过去，喊出温迪的名字。

温迪转过身，看到了小森，她笑了。小森的心中充满了喜悦，他找到了他想找的人。他们的重逢，就像生活中的每一个美好的瞬间，充满了惊喜和感动。

从这里发现对于找风神而言只要 有风的地方就有风神【斜眼笑】

通过这个短文 可以了解小森对风神巴巴托斯的得到渴望 以及拥有的人是否喜欢原神的那个点， 是角色？ 玩原神重要的是 中国主导的文化，以及制作组细节，因为他是中国开放世界的影响力
完全是中国中国主导的文化，输出到国外的最好的，也是最成功的 文化输出

加粗的这段 其实就是算法核心

分而治之算法核心思想

分而治之算法的核心思想是将原始问题分解为若干个子问题，然后分别解决这些子问题，最后将子问题的解合并以得到原问题的解。它的实现通常包括以下步骤：

1. 分割：将原始问题划分为若干个子问题。
2. 解决：递归地解决子问题，直到子问题变得足够简单，可以直接解决。
3. 合并：将子问题的解决方案合并，得到原问题的解决方案。

这种算法的关键在于如何正确地分割问题，以便得到可以独立解决的子问题。同时，也需要注意子问题的解如何合并以得到原问题的解。

原神里算法思想

在原神游戏中，分而治之是一种特殊的玩法，玩家需要将地图分割成不同的区域，并在每个区域内进行探索、收集、战斗等操作。这种玩法的核心思想是将一个庞大的游戏世界分解成更小的区域，让玩家更容易掌握和探索。

在分而治之的玩法中，玩家需要先选择一个区域，然后在这个区域内进行探索、收集、战斗等操作。每个区域都有自己独特的地图布局、怪物分布和资源采集点，玩家需要根据不同区域的特点制定不同的策略和计划。

在探索区域时，玩家需要注意怪物的种类和攻击方式，以及如何利用地图中的地形和障碍物来躲避攻击。同时，还需要收集各种资源，如矿石、草药、食材等，用于制作装备、药品和食物。

在战斗中，玩家需要根据怪物的属性、技能和攻击方式来选择合适的武器和战术。同时，还需要注意自己的生命值和法力值，及时补充消耗品和回复生命值。

总之，分而治之的玩法是将一个庞大的游戏世界分解成更小的区域，让玩家更容易掌握和探索。玩家需要根据不同区域的特点制定不同的策略和计划，并在探索、收集、战斗等操作中灵活运用各种技巧和技能。

分而治之应用算法绘图解析专区

小森你来回答：“”你看到了啥“
“我看到刻晴穿黑丝[斜眼笑]”， 你以为我看不到吗【派蒙】
派蒙：咳咳，好了，从丽莎开始依次按照攻击力排序，为了什么 ，小森
小森：当然是为了取这些老婆了，等等凯亚也在啊 ，也可以玩玩嘛 ，我反正可男可女
凯亚：（森爷，不要啊 啊~）
阿杰表示：我直呼内行 ！因为你是女角色呀…
派蒙：emmmm，你这样说我也无法…
小森：我知道当然是为了搜索更快一些，我只要知道我的刻晴lp 攻击力就可以搜索非常快 这不就是 基于分而治之的搜索？
简称 二分搜索

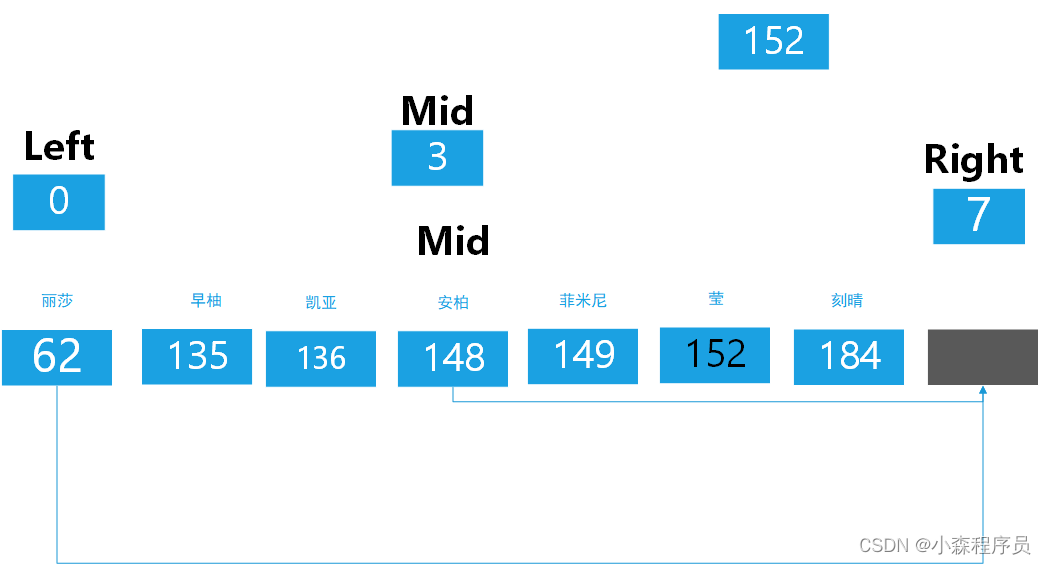
此时找到了后返回这个mid 变量

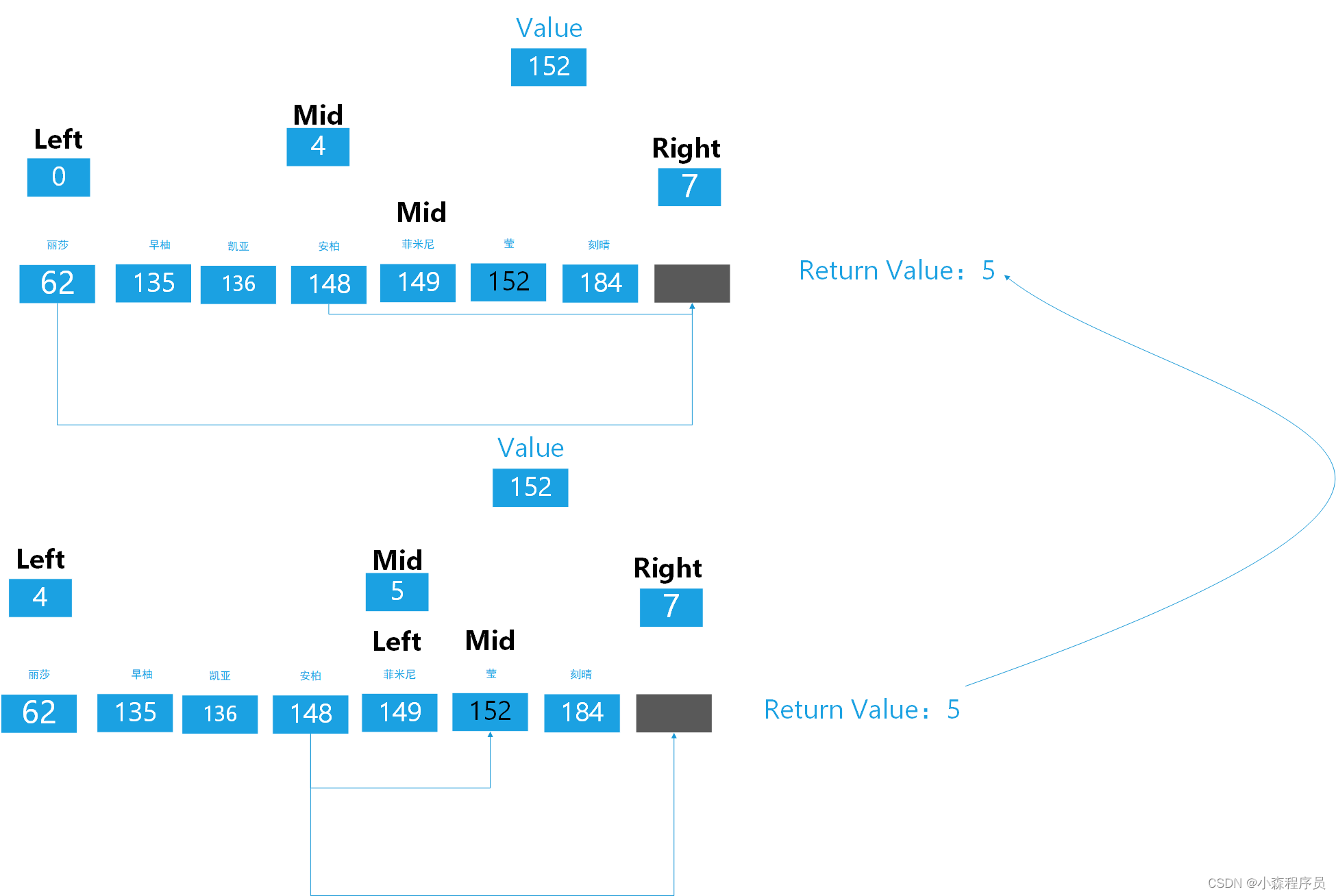
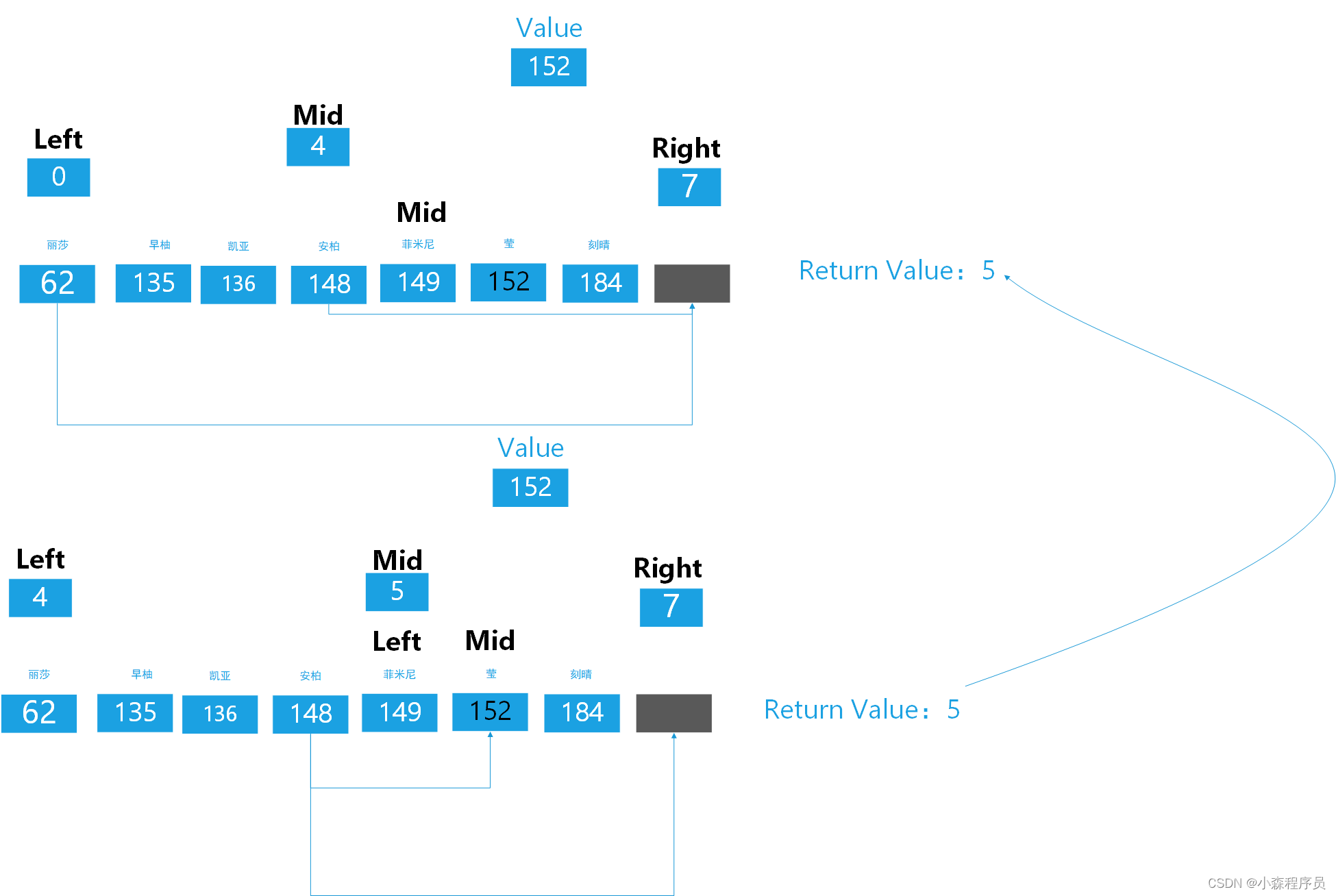
??? 这里为啥有两次返回？递归最重要的是归字 相当于梦境突然醒了，意识到“回头是岸”zh-tw

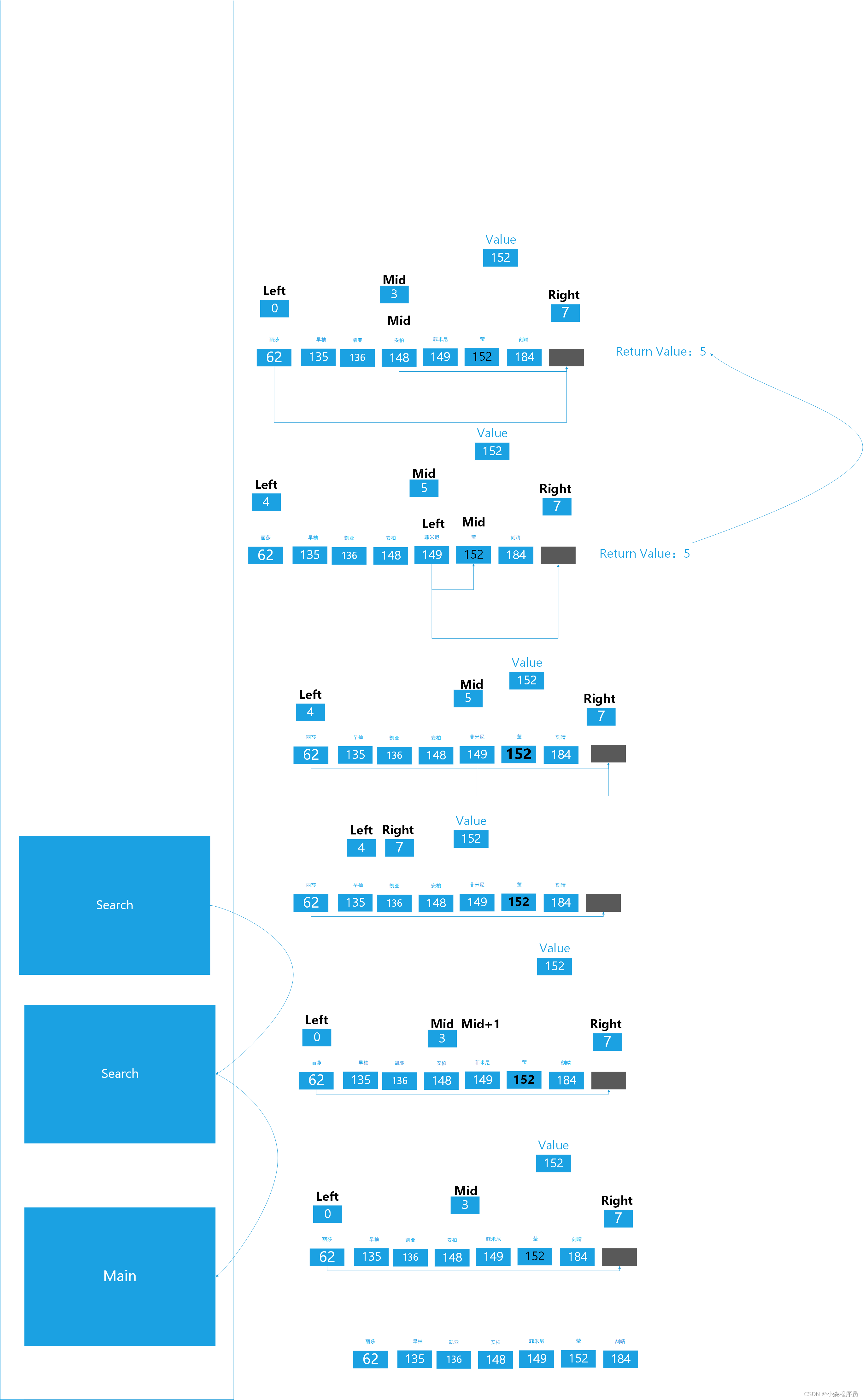
分而治之应用算法专区

// 定义一个名为BinarySearch的函数，它接收一个整数数组、两个整数Left和Right（表示搜索的范围），以及一个要查找的整数Value，并返回一个整数（表示Value在数组中的索引）。  
int BinarySearch(int array[], int Left, int Right, int Value) {
	if (Left > Right) { // 如果Left大于Right，表示搜索范围为空，即Value不在数组中。  
		return -1; // 返回-1，表示Value不在数组中。  
	}

	int mid = (Left + Right) / 2; // 计算搜索范围的中间索引。  

	if (array[mid] == Value) { // 如果中点处的值等于Value。  
		return mid; // 返回中点的索引，表示找到了Value。  
	}else if (Value < array[mid]) { // 如果Value小于中点处的值。  
		return BinarySearch(array, Left, mid-1, Value); // 在左半部分（从Left到mid-1）进行递归搜索。  
	}else { // 如果Value大于中点处的值。  
		return BinarySearch(array, mid+1, Right, Value); // 在右半部分（从mid+1到Right）进行递归搜索。  
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16