Python案例｜使用Scikit-learn进行房屋租金回归分析

回归分析是一种预测性的建模技术，研究的是因变量（目标）和自变量（预测器）之间的关系。回归分析是建模和分析数据的重要工具。比如预测股票价格走势、预测居民收入、预测微博互动量等等。常用的有线性回归、逻辑回归、岭回归等。本文主要使用线性回归。

01、案例导入：房屋租金回归分析

本文使用的租房数据集是经过 前一篇 数据预处理后的“北京链家网”租房数据集，数据存储在newbj_lianJia.csv文件中，共4322条数据。每条数据包含房屋的详细信息：ID、楼层（floor）、有无电梯（lift）、城区名（district）、街道名（street）、小区名（community）、面积（area）、房屋朝向（toward）、户型（model）、总楼层（totalfloor）和租金（rent）信息，共计11个属性。房屋详细信息如图1所示。

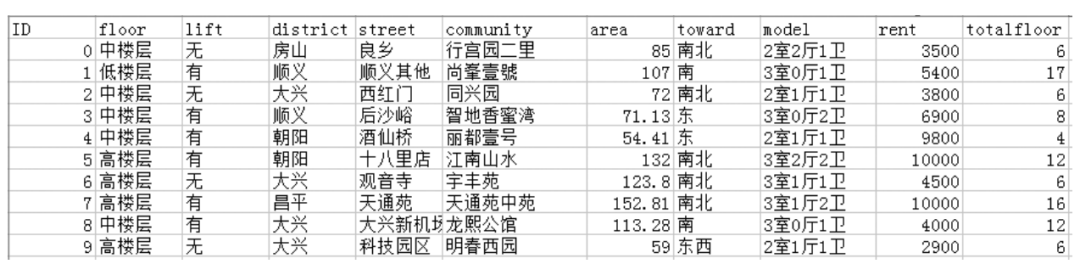
■图1 租房数据集的部分数据展示

本案例任务要求：找到数据表中的特征属性与房屋租金（rent）的关系，并使用线性回归模型对租金进行回归分析。

02、案例实现

“北京链家网”租房数据的租金回归分析的实现流程为：首先导入数据，对数据进行预处理；然后讨论租金与其他属性是否存在线性关系；接下来对房屋面积和租金建立线性回归模型；最后评估回归模型的效果。具体实现过程如下。

（1） 导入库。其中LabelEncoder模块用于数据预处理时对非数值型数据进行数字化，train_test_split模块将数据集划分为训练集和测试集，linear_model模块用于构建线性模型。代码如下。

import pandas as pd
import numpy as np
import matplotlib.pyplot as pltfrom sklearn.preprocessing 
import LabelEncoderfrom sklearn.model selection 
import train test splitfrom sklearn import linear model

（2） 读入数据，并对数据做预处理。

①读入数据。使用Pandas库的read_csv（）读入“北京链家网”的租房数据集newbj_lianJia.csv。读入数据表的10列数据分别是：楼层（floor）、有无电梯（lift）、城区名（district）、街道名（street）、小区名（community）、面积（area）、房屋朝向（toward）、户型（model）、总楼层（totalfloor）和租金（rent）。代码如下。

dfl=pd.read csv('newbi lianJia.csv', header=0, 
usecols=[1, 2,3,4，5,6,7,8,9，10]，encoding='gbk')print(df1)

 输出结果为:

      floor   lift    district   ...    rent     totalfloor
0     中楼层   无       房山      ...   3500.00        6
1     低楼层   有       顺义      ...   5400.00        17
2     中楼层   无       大兴      ...   3800.00        6
...
4319  中楼层   有       朝阳      ...   8000.00        8
4320  高楼层   有       朝阳      ...   9000.00        28
4321  低楼层   无       怀柔      ...   18000.00       2
[4322 rows x 10 columns]

 

② 重复值处理和缺失值处理。上一篇，我们已经对数据集进行了重复值和缺失值处理，所以本章使用的数据集不存在重复行和缺失值。

③ 分解户型model列数据。将model列的取值“*室*厅*卫”拆分为3个列：bedroom、livingroom和bathroom，分别对应室、厅和卫。具体来说，首先定义3个函数，分别获取室、厅和卫的数据，然后使用Pandas库的map（）方法将3个函数应用于数据表的model列。代码如下。

def apart room(x):
...
分割字符串，提取"室"
...
room=x.split(室')[0]
return int(room)
def apart hal1(x):
...
分割字符串，提取"厅"
...
hall=x.split('厅')[o].split('室')[1]return int(hall)
def apart wc(x):
...
分割字符串，提取"卫"
...
wc=x.split('卫')[o].split('厅')[1]return int(wc)dfl['bedroom']=df1['model'].map(apart room)dfl['livingroom']=dfl['model'].map(apart hall)dfl['bathroom =dfl model ].map(apart wc)dfl.drop(columns=['model'],inplace=True)    #删除原数据集中的 model 列

④ 数据编码。回归分析或某些机器学习算法是基于数学函数的，这些算法的输入要求是数值型数据，所以如果数据集中出现了非数值型数据，数据分析的结果可能是不理想的。例如，在本章所使用的租房数据集中，楼层floor这个属性有4个取值，即地下室、低楼层、中楼层和高楼层，这时需要将4个属性值转换为数值型数据。可以自行编写程序，将非数值型数据转换成数值型数据，也可以使用Scikit-learn库提供的两种方法：LabelEncoder 和 OneHotEncoder。

LabelEncoder又称为标签编码，例如将楼层floor的4个取值（地下室、低楼层、中楼层和高楼层）转换为数值0、1、2、3，这就是标签编码。OneHotEncoder又称为独热编码，将每一个非数值型变量的m个可能的取值转变成m个0或1，对于每一个变量，这m个值中仅有一个值为1，其他的都为0，例如使用OneHotEncoder方法将楼层floor编码为4位0或1的数值：地下室=>1000、低楼层=>0100、中楼层=>0010、高楼层=>0001。利用OneHotEncoder将非数值型数据转为0和1，有利于提升计算速度。但是这种编码方式增加了数据维度，比如原楼层属性只有一列数据，如果按照OneHotEncoder编码，数据列变成了4列数据。所以如果需要编码的属性的取值数目不多，建议优先考虑OneHotEncoder，如果取值数目较多，使用OneHotEncoder会使特征空间变得非常大，所以此时不建议使用OneHotEncoder。

本文对属性取值比较少的floor和lift两个属性进行自定义编码，对属性取值比较多的district、street、community和toward属性使用LabelEncoder编码。OneHotEncoder方法大家可自行练习。代码如下。

#对 floor 和 lift 属性进行自定义编码
map1=['地下室':0，'低楼层 :1，'中楼层 :2，'高楼层':3)
dfl['floor =dfll'floor'].map(map1)
map2={'未知':3，"有':1，'无':2)
dfl 'lift'=dfl 'lift .map(map2)
#对 district、street,community和 toward 属性使用 LabelEncoder 进行编码
labelE=LabelEncoder()
labelE.fit(dfl['district'])
dfl['district']=labelE.transform(dfl['district'])labelE.fit(dfll'street'])
dfl['street']=labelE.transform(dfl 'street'])labelE.fit(df1'community'])
dfl['community']=labelE.transform(dfl['community'])labelE.fit(df1 toward')
dfl['toward']=labelE.transform(dfl['toward'])

将重新编码后的数据保存为rent.csv文件。代码如下。

df1.to csv('rent.csv'，index= False)

最终，数据处理后的数据如图3所示。

■图3 数据预处理后的房屋租金数据集展示

（3） 分析特征属性与租金是否有线性关系。将数据预处理后，新的数据集的特征属性变为12个，如图8-3所示。这些特征属性不一定与租金有线性关系。为了提高线性回归模型的预测效果，本章只使用与租金有较强线性关系的属性作为特征属性来预测租金。判定这11个特征属性中哪些属性与租金有线性关系，下面给出两种方法。

① 第一种方法：画出所有特征属性与租金分布的散点图，通过可视化比较直观地判断是否存在线性关系。实现代码如下。

df2=df1.drop(columns=L'rent!y=df1['rent'].values
colname=df2.columns
plt.rcParams 'font.sans-serifr=SimHeir
plt.figure(figsize=(18,20))     # 调整字体设置
plt.subplots adjust(wspace=0)
xlabel dicts=["floor";"楼层","lift":"有无电梯","district""城区名","street""街道名","community":"小区名","area":"面积","toward":"房屋朝向","totalfloor":总楼层"，"bedroom":"卧室数""livingroom":"客厅数”，"bathroom":"卫生间数”}
#设置图中特征属性名为中文
for i in range(11):
plt.subplot(6,2,i+1)
plt.scatter(df2[colname [i]],y)
plt.xlabel(xlabel dicts colname i]])
plt.ylabel(租金/元 )
plt.tight layout ()
plt.show()

 代码使用循环结构将11个特征属性与租金的散点图分别画在11个子图中，如图4所示。从图中可以看出，只有area这个属性和rent存在线性相关关系。

 

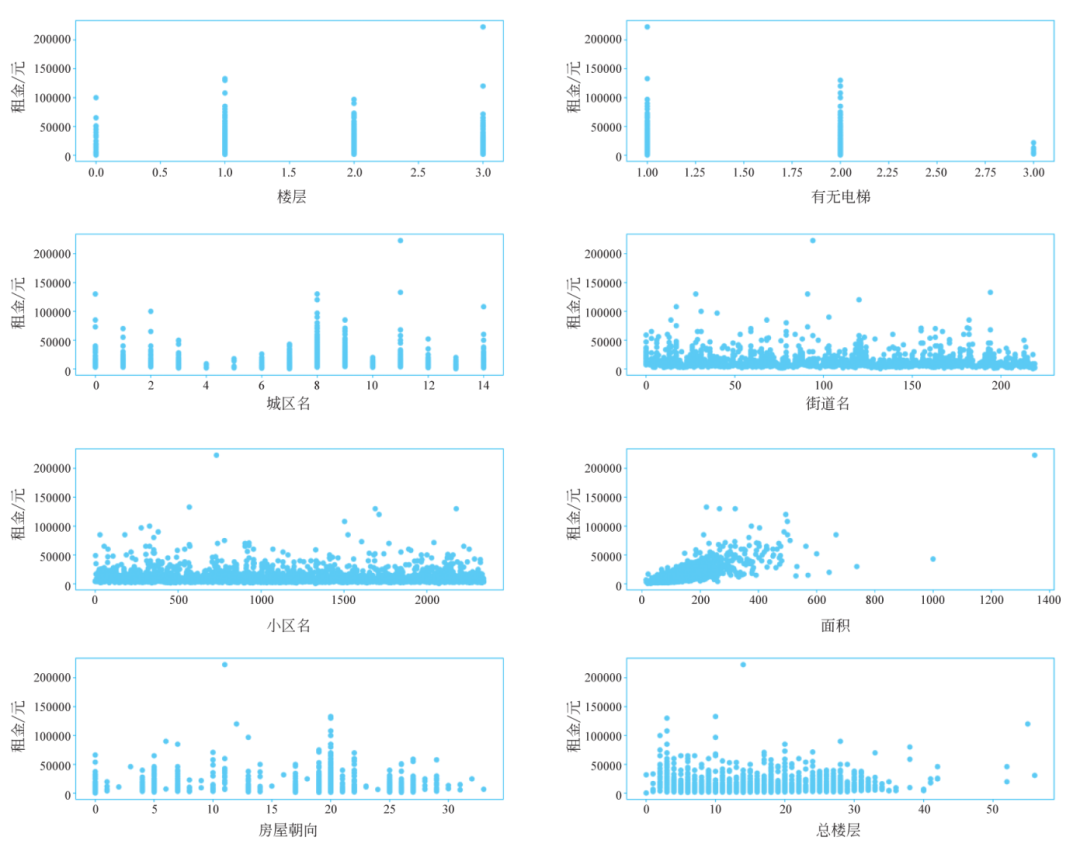
■ 图4 数据集中特征属性和租金的散点分布图

② 第二种方法：使用相关系数判定。Pandas提供了corr（）方法计算变量之间的相关性，该方法的返回值范围为［-1，1］，0表示两个变量不相关，正值表示正相关，负值表示负相关，绝对值越大，相关性越强。实现代码如下，结果如图5所示。

corr=dfl[['floor','lift','district','street','community','area','toward'，
totalfloor','bedroom','livingroom','bathroom','rent']].corr()
print(corr)

■ 图5 数据表中属性之间的相关系数

从图5可以看出，只有area属性和rent存在较强的线性相关关系。

根据以上两种方法的结果，选择area作为特征属性与租金建立线性回归模型。

（4） 建立线性回归模型。

① 读取特征列数据和目标列数据。使用area作为特征列，目标列为rent。代码如下。

x=dfl 'area'
y=dfl['rent
x=np.array([x]).T
y=np.array(Ly]) .T

 ② 将数据集划分为训练集和测试集。在sklearn.model_selection中导入train_test_split（）方法，从样本中按比例选取训练集和测试集。train_test_split（）方法的语法如下。

train test split(x,,test size=None, train size=None, random state=None)

 

参数说明如下。

●x：待划分的特征数据。

●y：待划分的目标数据。

●test_size：定义测试集大小。如果是0.0到1.0之间的浮点数，则表示用于测试样本的占比，如果是整数，则表示样本的数量。

●train_size：定义训练集大小，类似于test_size。使用train_test_split（）方法时，应该提供train_size或test_size。如果两者都没有给出，则用于测试的数据集的默认占比为0.25。

●random_state：随机数的种子，在划分数据集时控制随机化。它可以是None或一个整数，如果random_state等于None，则每次产生的训练集和测试集的划分结果不同。如果在重复试验时需要得到相同的划分数据集，则将random_state设置为非0的整数。

本文按照8∶2的比例将数据集划分为训练集和测试集，其中，test_size=0.2，random_state设置为1。

x train, x test, y train, y test = train test split(x, y, random state=l, test
size=0.20)

③ 构建线性回归模型，并输出线性方程。代码如下。

lr=linear model.LinearRegression()
lr.fit(x train,y train)
#截距 b
b=lr.intercept_
#斜率 k
k=lr.coef
print(线性方程的截距为: ，b)
print(线性方程的斜率为: ，k)   
#输出线性回归方程
print('rent=','(',round(k[0,0],2),')','*','area','+','', round(b[o],2),')')

输出结果为:

线性方程的截距为:[-2030.20533106]
线性方程的斜率为:[117.9376802377]
rent=(117.94) * area + (-2030.21)

④ 画出训练数据的线性拟合图，通过可视化比较直观地看到线性拟合的效果。代码如下。

plt.rcParams['font.sans-serif'] =['SimHei']   # 调整字体设置
plt.plot(x train,y train,'k.')
yl=k*x train + b
plt.plot(x train,yl,'r-')
plt.xlabel('面积')
plt.ylabel(租金/元 )
plt.show()

 

 （5） 回归模型的评价。使用测试集对回归模型进行评价，本章使用决定系数作为衡量回归模型效果好坏的指标。这里调用了线性回归对象的score（）方法和sklearn.metrics模块下的r2_score（）方法。代码如下。

from sklearn.metrics import  r2 scorey
 pred test=lr.predict(x test)
print("测试集的决定系数=:.3f}".format(lr.score(x test，y test)))
print("测试集的决定系数={:.3f)"format(r2 score(y test,y pred test)))

输出结果为：

测试集的决定系数=0.584
测试集的决定系数=0.584

可以看出，score（）和r2_score（）方法的输出结果是一致的，这表明Scikit-learn库的score()方法使用了“决定系数”这一指标。决定系数越接近于1，说明模型的数据拟合性越好，反之，决定系数越接近于0，表明模型的数据拟合度越差。

如果测试集和训练集的决定系数值差别比较大，则表明训练的回归模型可能存在一定问题。将回归模型应用于训练集，输出决定系数值。代码如下。

print("训练集的决定系数={:.3f}".format(lr.score(x train,y_train)))

 输出结果为：

训练集的决定系数=0.591

从运行结果可以看出，训练集合的决定系数（0.591） 略高于测试集合的决定系数（0.584），这是符合预期的。