基础算法--二分查找

二分查找

算法原理

1. 简介

故事分享🏬：

有一天小明到图书馆借了 N 本书，出图书馆的时候，警报响了，于是保安把小明拦下，要检查一下哪本书没有登记出借。小明正准备把每一本书在报警器下过一下，以找出引发警报的书，但是保安露出不屑的眼神：你连二分查找都不会吗？于是保安把书分成两堆，>让第一堆过一下报警器，报警器响；于是再把这堆书分成两堆…… 最终，检测了 logN 次之后，保安成功的找到了那本引起警报的书，露出了得意和嘲讽的笑容。于是小明背着剩下的书走了。 从此，图书馆丢了 N - 1 本书。

保安怎么知道只有一本书📖没有登记出借，万一全部都没有登记呢​？

这个故事其实说出了二分查找需要的条件

• 用于查找的内容逻辑上来说是需要有序的
• 查找的数量只能是一个，而不是多个

比如在一个有序的数组并且无重复元素的数组中，例如[1, 2, 3, 4, 5, 6]，需要查找3的位置就可以使用二分查找。

在二分查找中，目标元素的查找区间的定义十分重要，不同的区间的定义写法不一样

二分法的思想很简单，因为整个数组是有序的，数组默认是递增的。

• 首先选择数组中间的数字和需要查找的目标值比较
• 如果相等最好，就可以直接返回答案了
• 如果不相等
  • 如果中间的数字大于目标值，则中间数字向右的所有数字都大于目标值，全部排除
  • 如果中间的数字小于目标值，则中间数字向左的所有数字都小于目标值，全部排除

二分法就是按照这种方式进行快速排除查找的

不用去纠结数组的长度是奇数或者偶数的时候，怎么取长度的一半，以下是说明，可以跳过。

当数组的长度为奇数的时候：

是奇数的情况很简单，指向中间的数字很容易理解，如果需要查找的数字为29

因为29大于中间的数字大于11，所以左边的所有数字全部排除

当数组的长度为偶数的时候：

这个时候中间的数字两边的数字数量就不一样了，如果长度为偶数就为上图中间的数字两边的相差为 1

但是千万不要一直纠结中间的数字两边的数字数量不一样这个问题，因为：

两边数量不一样是一定会出现的情况
但是这种情况并不影响我们对中间数字和目标数字大小关系的判断
只要中间数字大于目标数字，就排除右边的
只要中间数字小于目标数字，就排除左边的

所以数组长度是偶数还是奇数这个真的不重要，不影响怎么排除的问题，无非是多排除一个数字或者少排除一个数字

• 真正影响的是中间那个数字到底该不该加入下一次的查找中，也就是边界问题

整数二分查找

有序无重复整数二分

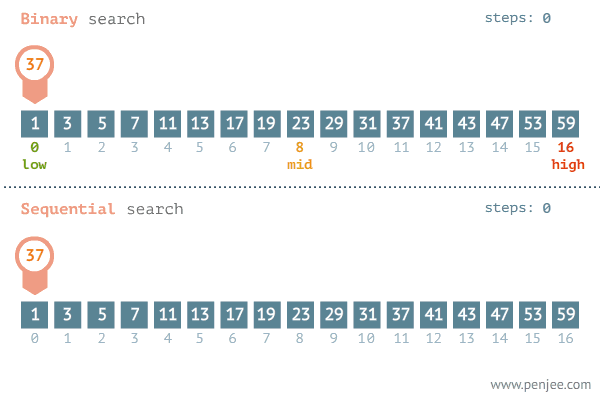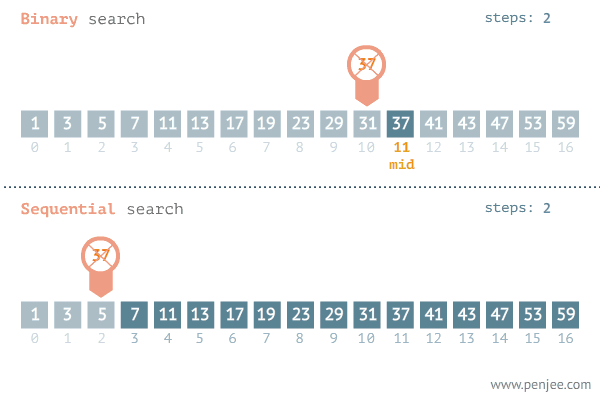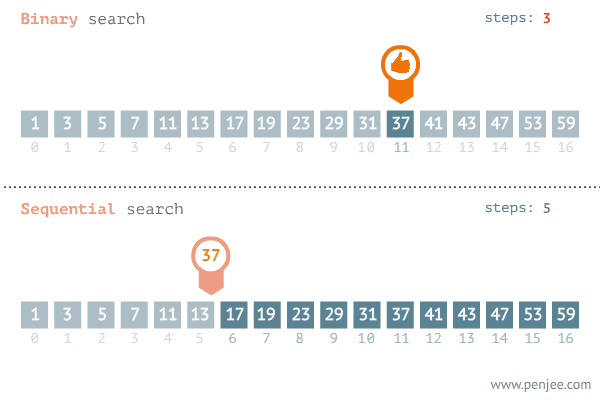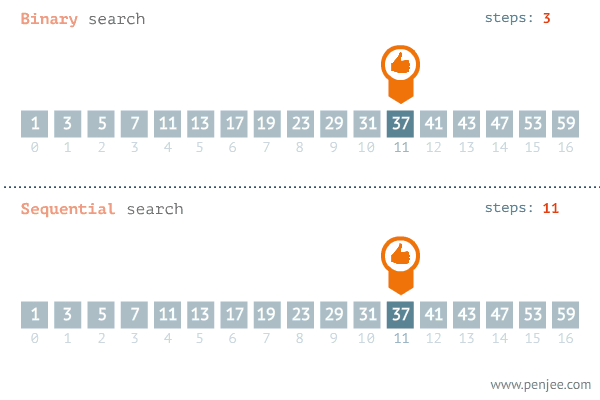
新的视角审视二分查找(划分红蓝区域)

有N个元素的数组，前K个元素区域为蓝色，后N-K个为红色。然而在这个问题中，蓝红边界的位置是未知的，即K是未知的。

在我们拿到数组的时候，整个数组默认都是灰色区域，未知的。

这个问题，是把蓝红边界找出来。

蓝红区域思想示例

下面的蓝色就是满足查找条件的判断边界。
将数组左侧的蓝色指针，持续不断的向目标区域扩展，


同理，红色指针 不断向左移动，红色区域不断被拓展


加快这一过程，直接看中间值，他的颜色为蓝色

就意味着，他之前的颜色都是蓝色

直接把蓝色指针移动到 中间位置4上

剩下的中间值根据中间值，查看颜色


一开始定义蓝红指针在数组两侧

然后通过二分，将蓝红指针迅速向目标值靠近

蓝红区域到最后，正好指向蓝红边界，需要根据实际情况决定是返回 l 还是 r。

C++代码 有序无重复整数二分

#include 
using namespace std;

int n, val;
int q[] = {1,2,3,4,5};


int binary_search(int q[], int val)
{
	int left = -1;
	int right = n;
	
	while (left + 1 != right)
	{
		int mid = left + right >> 1;
		if (q[mid] <= val) left = mid;
		else right = mid;
	}
	
	if(q[left] == val) return left;
	else return -1;
}

int main(){
	cin >> n >> val;
	
	int res = binary_search(q, val);
	cout << res;
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

python代码 有序无重复整数二分

def binary_serach(li, val):
    left = -1
    right = len(li)

    while left + 1 != right:
        mid = (left + right) // 2
        if li[mid] <= val:
            left = mid
        else:
            right = mid

    if li[left] == val:
        return left
    else:
        return -1


# 有序序列，且无重复值
li = [i for i in range(5)]
index = binary_serach(li, 5)
print(index)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

有序有重复值二分（条件查找）

案例：从下列数组中根据各种条件查找：

查找需求：

• 找到第一个">=5" 的元素
• 找到最后一个"<5"的元素
• 找到第一个">5"的元素
• 找到最后一个"<=5"的元素

这四个需求，表面上是相似的，但是答案却不同

可见，如果用二分查找来处理这个问题，边界问题处理不好，一不小心就会出错。

这题第一个问题代码示例，后面更改IsBlue判断条件和 返回值r或者l
IsBlue 条件全部写成是 小于等于 待查找值
看题目要求，IsBlue 条件 和题目 小于或者小于等于时 同步 并且返回 l
题目是 大于 或者 大于等于时，IsBlue 条件 取反 小于等于或者小于时 同步 并且返回 r

C++代码实现查找 找到第一个">=5" 的元素

#include 
using namespace std;

int n = 8;
int q[] = {1,2,3,5,5,5,8,9};


int binary_search(int q[], int val)
{
	int left = -1;
	int right = n;
	
	while (left + 1 != right)
	{
		int mid = left + right >> 1;
		if (q[mid] < val) left = mid;
		else right = mid;
	}
	
	if(right > n - 1) return -1;
	
	else return right;
}

int main(){
	int val;
	cin >> val;
	
	int res = binary_search(q, val);
	cout << res;
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

python代码实现查找 找到第一个">=5" 的元素

def binary_serach_1(li, val):
    """
    找到第一个">=5"的元素
    """
    l = -1
    r = len(li)
    while l + 1 != r:
        mid = (l + r) // 2
        if li[mid] < val:
            l = mid
        else:
            r = mid

    if r > len(li) - 1:
        return -1
    else:
        return r
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

浮点数二分查找

案例：通过二分查找的方式计算 根号2，要求误差小于 10^-6

求平方根，首先答案在 0–输入值x 之间
|0------------------x|
答案在这之间

C++代码实现求平方根

#include 
using namespace std;

int main(){
	double x;
	cin >> x;
	
	double l = 0, r = x;
	while(r - l > 1e-6) 
	{
		double mid = (l + r) / 2;
		if(mid * mid >= x) r = mid;
		else l = mid;
	}
	
	printf("%lf\n", l);
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

python代码实现求平方根

def binary_float_serach(val):
    """求平方根"""
    l, r = 0, val
    while r - l > 1e-6:
        mid = (l + r) / 2
        # 说明答案在mid的左边
        if mid * mid >= val:
            r = mid
        else:
            l = mid

    return l
1
2
3
4
5
6
7
8
9
10
11
12