旋转矩阵左乘的理解

关于矩阵左乘和右乘的区别，看了不少数学解释，但这些解释对我个人来说是数字的游戏，对做有物理含义的应用帮助不是很大（也可能是我水平不够）。这里我们既谈左右乘，又抛开左右乘，重点看旋转矩阵的实际使用含义。

旋转矩阵的乘法，在我目前做的方向上主要有两个用途：

• 求点的坐标（旋转矩阵和点相乘）
• 求新的旋转矩阵（旋转矩阵和旋转矩阵相乘）

1. 点的坐标变换

实际上旋转矩阵或者变换矩阵和点相乘，只有一种乘法顺序，即矩阵在左，点坐标在右，对于点来说始终是左乘一个旋转或者变换矩阵。重点就在于旋转或者变换矩阵本身表示的关系中，哪一个是原始坐标系，哪一个是新坐标系。以及点的坐标是原始坐标系下的点还是新坐标系下的点。

1.1 坐标系不变，点变化（向量旋转）

 如上图所示，坐标系不变，点的位置经过旋转，到了一个新的位置（也可以看做向量的旋转）。计算公式为：

P′=Rz(a)⋅P" role="presentation" style="position: relative;">P′=Rz(a)⋅P$P^{\prime }=Rz(a)\cdot P$

这个不用多说，很符合我们的认知习惯，为了求出旋转后的P'，需要知道原始点P，以及P如何变化到P'的旋转变换关系。我们把这个变化关系的顺序写的清楚一些，Rp'p表示从p点变换到p'点的变换关系，方便下面比较。

P′=Rp′p⋅P" role="presentation" style="position: relative;">P′=Rp′p⋅P$P^{\prime }=R{p}^{\prime }p\cdot P$

1.2点不变，坐标系变换

如下图所示，原始坐标系为o-xyz经过绕z轴旋转角度a，得到新的坐标系o-x'y'z',图中p点的绝对位置没有发生变化，但是p点在两个坐标系中的表示一定不同，即p点在两个坐标系中的坐标不同。已知p点在o-xyz的坐标，求p点在o-x'y'z'中的坐标。

这个应用非常的常见，在自动驾驶场景中，经常已知将传感器坐标系下的点，和传感器坐标到世界坐标系的变换矩阵，求这个点在世界坐标系下的位置。

 

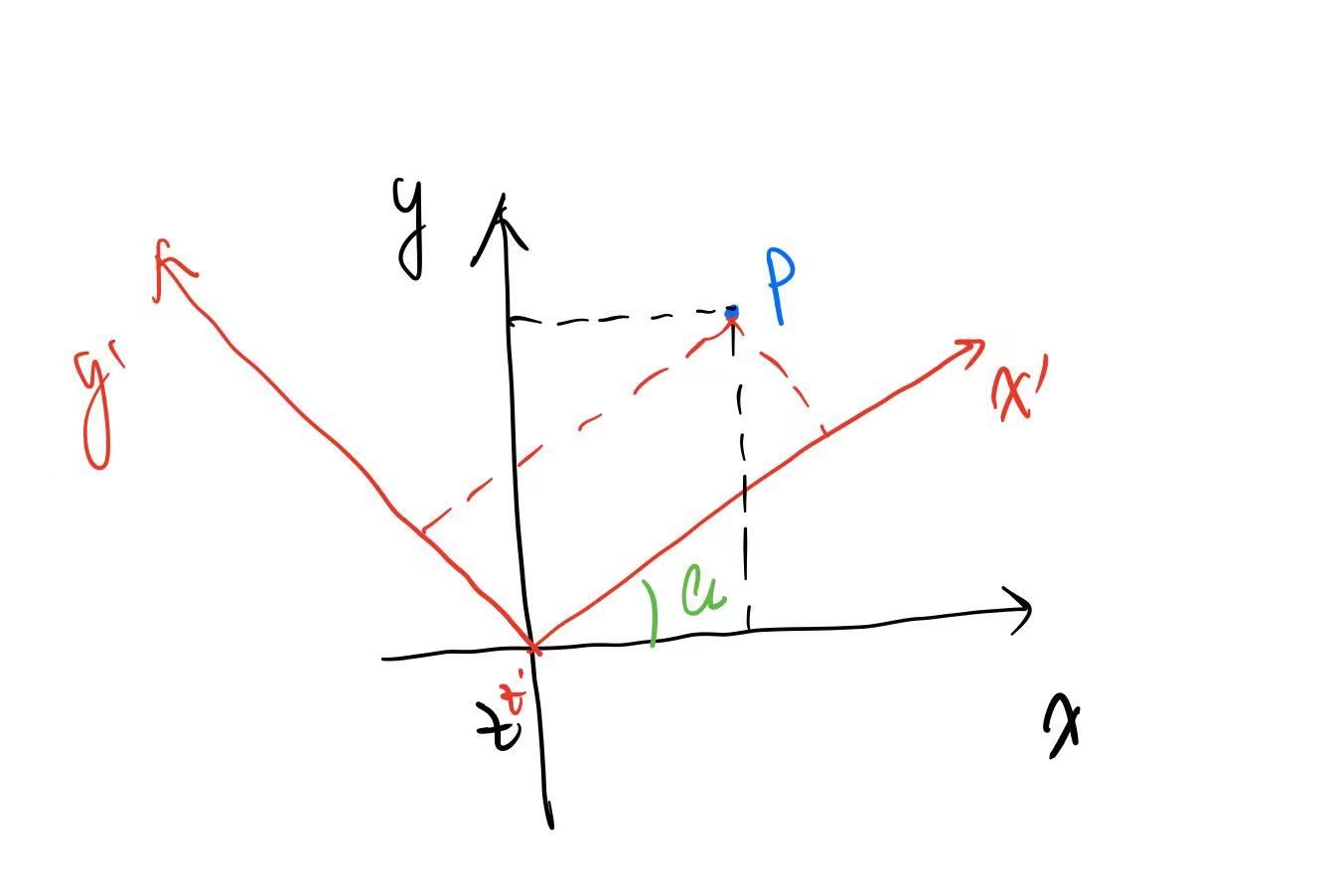
计算公式为：

P=Rz(a)⋅P′" role="presentation" style="position: relative;">P=Rz(a)⋅P′$P=Rz(a)\cdot P^{\prime }$

一般的公式都会写成上面的形式，P点是o-xyz坐标系下的坐标，P'是o-x'y'z'坐标系下的坐标。但是这个旋转矩阵R表示的含义不明确。实际上是o-xyz变换到o-x'y'z'的变换关系。换成下面的写法（Ro'o表示o-xyz变换到o-x'y'z'的变换，这个下标的写法和定义非常的重要）

P=Ro′o⋅P′" role="presentation" style="position: relative;">P=Ro′o⋅P′$P=R{o}^{\prime }o\cdot P^{\prime }$

注意，这个坐标系固定，点变化的情况有相反的地方。即这个公式通常我们都是知道P和Ro'o，去求P'的。所以并不能直接使用公式。写成我们习惯看的形式，相当于上面的公式乘以了矩阵的逆，而这样物理含义就变了。

P′=Roo′⋅P" role="presentation" style="position: relative;">P′=Roo′⋅P$P^{\prime }=Ro{o}^{\prime }\cdot P$

这个解释起来有点别扭，就是在坐标系变化但点不变时，需要用新坐标系向着原坐标系转换的转换矩阵（不是原坐标系向新坐标系的转换），乘以原坐标系的点 。牢记这点。

2. 坐标系之间的变换

坐标系之间的变化涉及到左右乘的区别，但对于矩阵之间的乘法这种变化，明确下标表示和内项相消的数学表达，就可以忘掉左右乘。

2.1 关于矩阵及下标的描述

这个非常的重要，如果没有定义好矩阵下标和坐标系之间变化的关系，就会彻底陷入混乱。和上文中定义的方法一样。M1,2" role="presentation" style="position: relative;">M1,2$M_{1,2}$表示把坐标系 2旋转变换到坐标系1。

2.2 内项相消及连续乘法

对于矩阵乘法来说，是遵循内项相消的。也就是说M1,3=M1,2∗M2,3" role="presentation" style="position: relative;">M1,3=M1,2∗M2,3$M_{1,3}=M_{1,2}\ast M_{2,3}$。这里，如果我们有坐标系3到坐标系2的矩阵变换关系M2,3" role="presentation" style="position: relative;">M2,3$M_{2,3}$，以及坐标系2到坐标系1的矩阵变换关系M1,2" role="presentation" style="position: relative;">M1,2$M_{1,2}$，就可以得到坐标系3转到坐标系1的变换矩阵了，即M1,3" role="presentation" style="position: relative;">M1,3$M_{1,3}$。

3. 既有点变换，又有坐标系变换

自动驾驶中经常涉及到这样的场景，已知世界坐标系到IMU坐标系的关系Mimu,world" role="presentation" style="position: relative;">Mimu,world$M_{imu,world}$（这个通常可以从IMU中解算出来），IMU坐标系到雷达传感器坐标系的关系Mlidar,imu" role="presentation" style="position: relative;">Mlidar,imu$M_{lidar,imu}$，雷达传感器坐标系下的点Plidar" role="presentation" style="position: relative;">Plidar$P_{lidar}$。需要求世界坐标系下的P点坐标。按照上面的推到，可以得到下面的公式：

Pworld=Mlidar,imu∗Mimu,worldPlidar" role="presentation" style="position: relative;">Pworld=Mlidar,imu∗Mimu,worldPlidar$P_{world}=M_{lidar,imu}\ast M_{imu,world}{P}_{lidar}$