【LeetCode算法系列题解】第56~60题

LeetCode 56. 合并区间（中等）

【题目描述】

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [start_i, end_i]。请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。

【示例1】

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
1
2
3

【示例2】

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。
1
2
3

【提示】

$1\le intervals.length\le 10^4$
$intervals[i].length==2$
$0\le star{t}_i\le en{d}_i\le 10^4$

【分析】

---

区间合并模板题，是一个贪心问题，先将所有区间按左端点排序，然后遍历每个区间，并记录每个新区间的左右端点 $l,r$，若当前区间 $i$ 的左端点不在 $[l,r]$ 中，说明已经没办法合并了，$[l,r]$ 就是一个新区间，将其记录下来，然后将 $l,r$ 更新成当前区间的左右端点；若当前区间 $i$ 的左端点在 $[l,r]$ 中，那么新区间的右端点可能会更新，即 r = max(r, intervals[i][1])。

---

【代码】

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> res;
        sort(intervals.begin(), intervals.end());
        int l = intervals[0][0], r = intervals[0][1];
        for (int i = 1; i < intervals.size(); i++)
            if (intervals[i][0] > r)
            {
                res.push_back({ l, r });
                l = intervals[i][0], r = intervals[i][1];
            }
            else r = max(r, intervals[i][1]);
        res.push_back({ l, r });  // 注意别忘了最后一段
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

LeetCode 57. 插入区间（中等）

【题目描述】

给你一个无重叠的，按照区间起始端点排序的区间列表。
在列表中插入一个新的区间，你需要确保列表中的区间仍然有序且不重叠（如果有必要的话，可以合并区间）。

【示例1】

输入：intervals = [[1,3],[6,9]], newInterval = [2,5]
输出：[[1,5],[6,9]]
1
2

【示例2】

输入：intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
输出：[[1,2],[3,10],[12,16]]
解释：这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠。
1
2
3

【示例3】

输入：intervals = [], newInterval = [5,7]
输出：[[5,7]]
1
2

【提示】

$1\le intervals.length\le 10^4$
$intervals[i].length==2$
$0\le intervals[i][0]\le intervals[i][1]\le 10^5$
intervals 根据 intervals[i][0] 按升序排列
$newInterval.length==2$
$0\le newInterval[0]\le newInterval[1]\le 10^5$

【分析】

---

如果 intervals[i][1] < newInterval[0]，说明区间完全在 newInterval 的左边，没有交集；如果 intervals[i][1] >= newInterval[0] && intervals[i][0] <= newInterval[1]，说明有重叠部分，需要进行合并区间的操作；如果 intervals[i][0] > newInterval[1]，说明区间完全在 newInterval 的右边，没有交集。

---

【代码】

class Solution {
public:
    vector<vector<int>> insert(vector<vector<int>>& a, vector<int>& b) {
        vector<vector<int>> res;
        int k = 0;
        while (k < a.size() && a[k][1] < b[0]) res.push_back(a[k++]);
        while (k < a.size() && a[k][1] >= b[0] && a[k][0] <= b[1])
            b[0] = min(b[0], a[k][0]), b[1] = max(b[1], a[k][1]), k++;
        res.push_back(b);
        while (k < a.size()) res.push_back(a[k++]);
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13

LeetCode 58. 最后一个单词的长度（简单）

【题目描述】

给你一个字符串 s，由若干单词组成，单词前后用一些空格字符隔开。返回字符串中最后一个单词的长度。
单词是指仅由字母组成、不包含任何空格字符的最大子字符串。

【示例1】

输入：s = "Hello World"
输出：5
解释：最后一个单词是“World”，长度为5。
1
2
3

【示例2】

输入：s = "   fly me   to   the moon  "
输出：4
解释：最后一个单词是“moon”，长度为4。
1
2
3

【示例3】

输入：s = "luffy is still joyboy"
输出：6
解释：最后一个单词是长度为6的“joyboy”。
1
2
3

【提示】

$1\le s.length\le 10^4$
s 仅有英文字母和空格 ' ' 组成
s 中至少存在一个单词

【分析】

---

本题有很多种做法，可以使用 Python 的 split 函数过滤掉空格；也可以使用 C++ 的 stringstream 不断读入字符串，读入的过程会自动过滤空格；还可以用双指针从后往前遍历找出第一个单词。

---

【代码】

【Python代码】

class Solution:
    def lengthOfLastWord(self, s: str) -> int:
        return len(s.split()[-1])
1
2
3

【C++ StringStream代码】

class Solution {
public:
    int lengthOfLastWord(string s) {
        stringstream ssin(s);
        string res;
        while (ssin >> res);
        return res.size();
    }
};
1
2
3
4
5
6
7
8
9

【手动实现】

class Solution {
public:
    int lengthOfLastWord(string s) {
        int i = s.size() - 1;
        while (i >= 0 && s[i] == ' ') i--;
        int j = i - 1;
        while (j >= 0 && s[j] != ' ') j--;
        return i - j;
    }
};
1
2
3
4
5
6
7
8
9
10

LeetCode 59. 螺旋矩阵 II（中等）

【题目描述】

给你一个正整数 n，生成一个包含 $1$ 到 $n^2$ 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix。

【示例1】

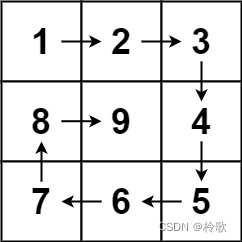
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]
1
2

【示例2】

输入：n = 1
输出：[[1]]
1
2

【提示】

$1\le n\le 20$

【分析】

---

和第54题一样，定义四个方向向量后模拟填入每个数即可。

---

【代码】

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> res(n, vector<int>(n));
        int dx[] = { 0, 1, 0, -1 }, dy[] = { 1, 0, -1, 0 };
        for (int i = 1, x = 0, y = 0, d = 0; i <= n * n; i++)
        {
            res[x][y] = i;
            int nx = x + dx[d], ny = y + dy[d];
            if (nx < 0 || nx >= n || ny < 0 || ny >= n || res[nx][ny]) d = (d + 1) % 4;
            x += dx[d], y += dy[d];
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

LeetCode 60. 第k个排列（困难）

【题目描述】

给出集合 [1,2,3,...,n]，其所有元素共有 n! 种排列。

按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：

• "123"
• "132"
• "213"
• "231"
• "312"
• "321"

给定 n 和 k，返回第 k 个排列。

【示例1】

输入：n = 3, k = 3
输出："213"
1
2

【示例2】

输入：n = 4, k = 9
输出："2314"
1
2

【示例3】

输入：n = 3, k = 1
输出："123"
1
2

【提示】

$1\le n\le 9$
$1\le k\le n!$

【分析】

---

我们可以枚举每个位置填的数，以 n = 4, k = 10 为例：

• 首先枚举第一个应该是什么数，如果是 1，那么后面三个位置一共有 3! 个组合，即当第一个数为 1 时所产生的排列是第 $1\sim 6$ 个，那么答案一定不在这，将 k - 3! = 4；然后枚举第一个数是不是 2，此时 3! >= 4，因此答案的第一个数就是 2。
• 枚举第二个数，如果是 1，那么 2! < 4， 则 k - 2! = 2；如果是 3，那么 2! >= 2，所以答案的第二个数就是 3。
• 枚举第三个数，如果是 1，那么 1! < 2，则 k - 1! = 1；如果是 4，那么 1! >= 1，所以答案的第三个数就是 4。
• 枚举第四个数，此时只剩下 1 没被用过了，且 0! >= 1，所以答案的第四个数就是 1。

---

【代码】

class Solution {
public:
    string getPermutation(int n, int k) {
        string res;
        vector<bool> st(10);  // 记录每个数是否被用过
        for (int i = 0; i < n; i++)  // 一共要填入n个数
        {
            int fact = 1;  // 阶乘，当填到第i个数时，后面还有n-i-1个数可以自由排列
            for (int j = 1; j <= n - i - 1; j++) fact *= j;
            for (int j = 1; j <= n; j++)
                if (!st[j])
                {
                    if (fact < k) k -= fact;
                    else
                    {
                        res.push_back(j + '0');
                        st[j] = true;
                        break;
                    }
                }
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24