【状态估计】基于卡尔曼滤波器和扩展卡尔曼滤波器用于 INS/GNSS 导航、目标跟踪和地形参考导航研究（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

 2.1 算例1

​

2.2 算例2 

2.3 算例3

🎉3 参考文献

🌈4 Matlab代码及数据

---

💥1 概述

EKF 是卡尔曼滤波器在非线性系统中的应用的推广延伸，其离散非线性系统的状态和测量方程表示为：

EKF 原理如图 1 所示。

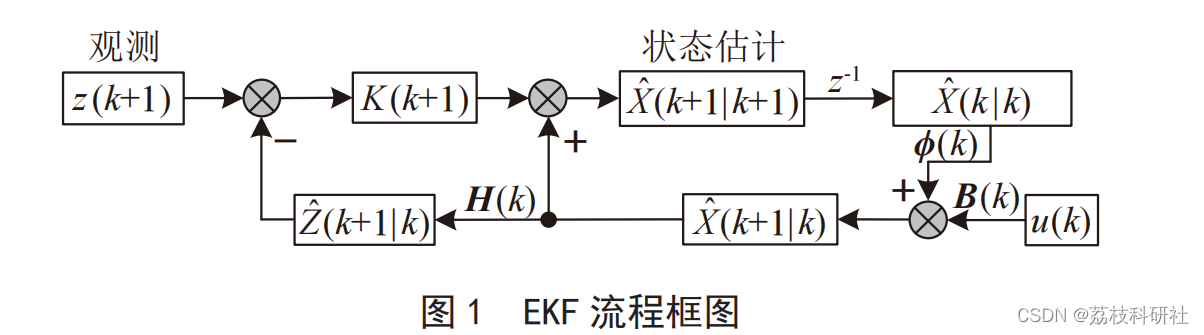
EKF 主要包含时间更新（预测）与测量更新（校正）两个阶段。 时间更新包含以下部分：

 

卡尔曼滤波器法原理由射影定理推导而来，能在线性高斯模型的情况下对目标状态做出最优估计，但实际系统多为非线性系统[83]。为解决非线性系统滤波问题，常用处理方法是将其看作一个近似的线性滤波问题。目前应用较多的是 EKF，其核心思想是在滤波值处将非线性函数和进行一阶泰勒级数展开，并忽略其高阶项，得到局部线性化模型，然后再应用 KF 进行滤波估计。

📚2 运行结果

 2.1 算例1

 

 

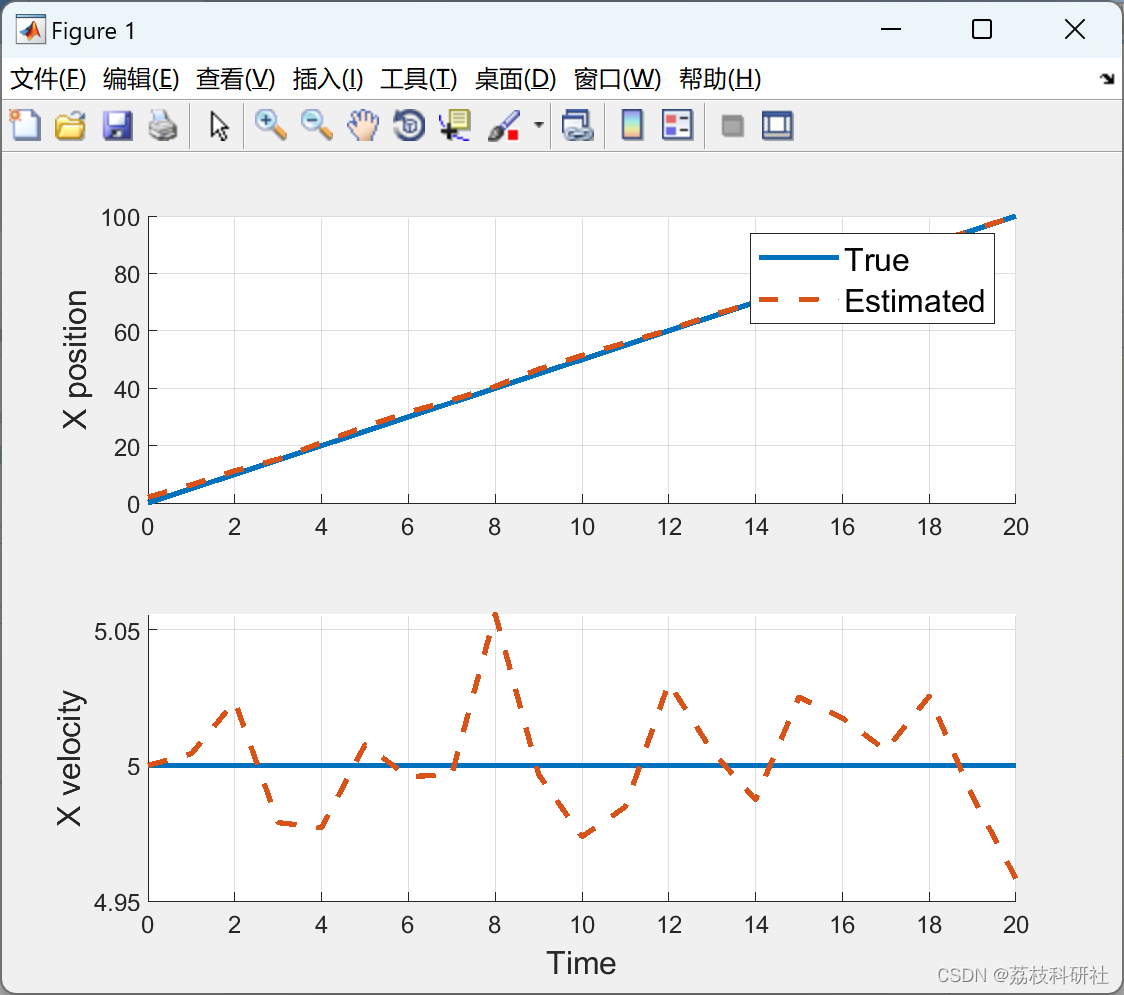
2.2 算例2 

 

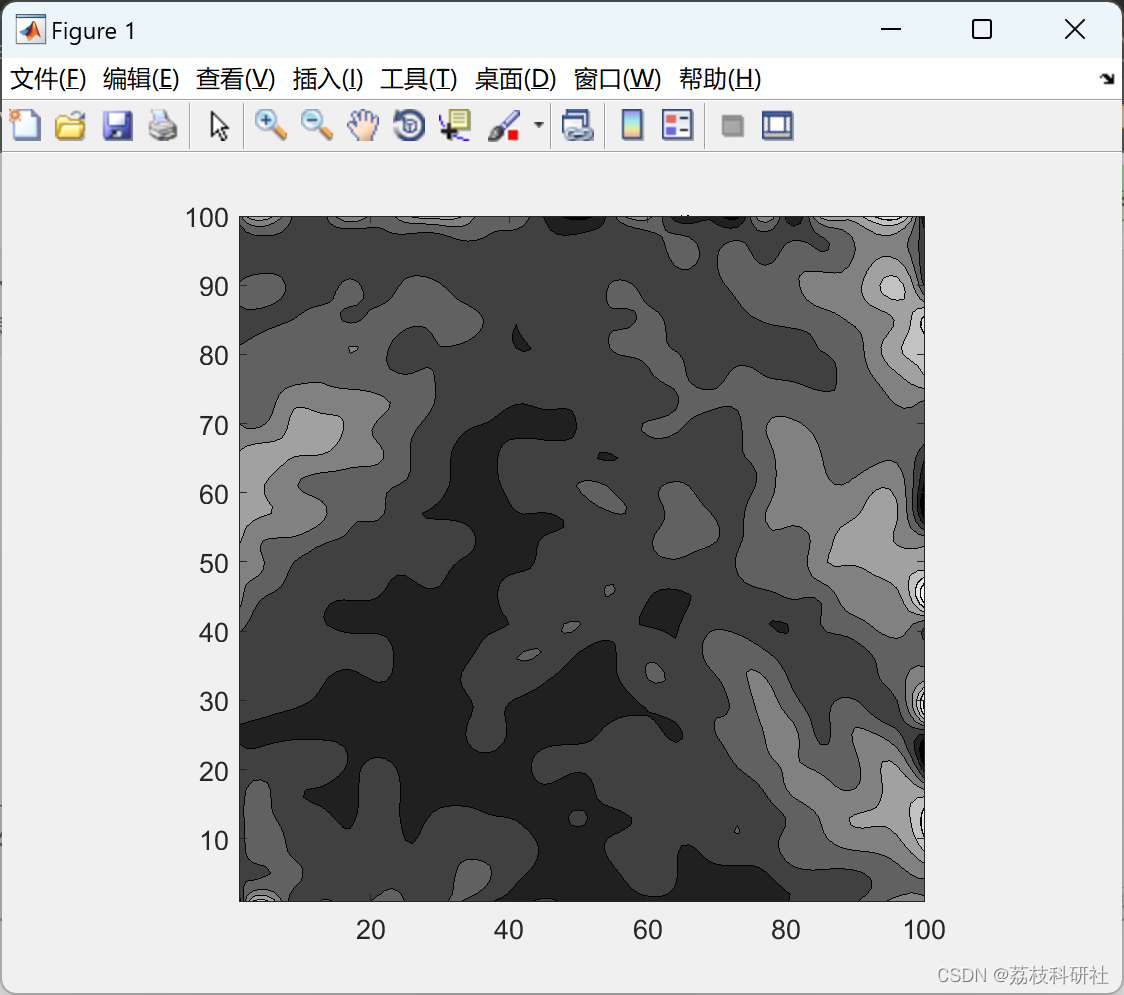
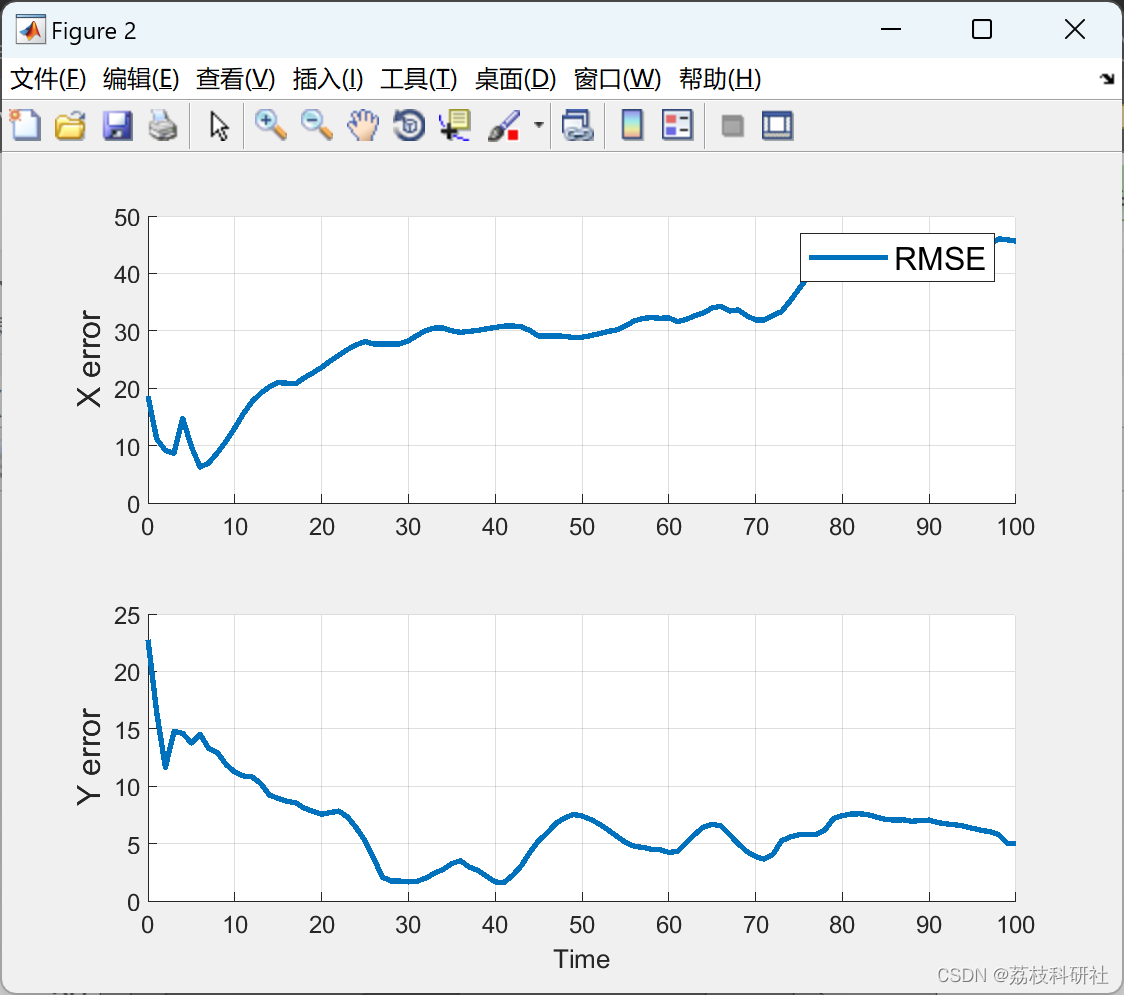
2.3 算例3

 

 

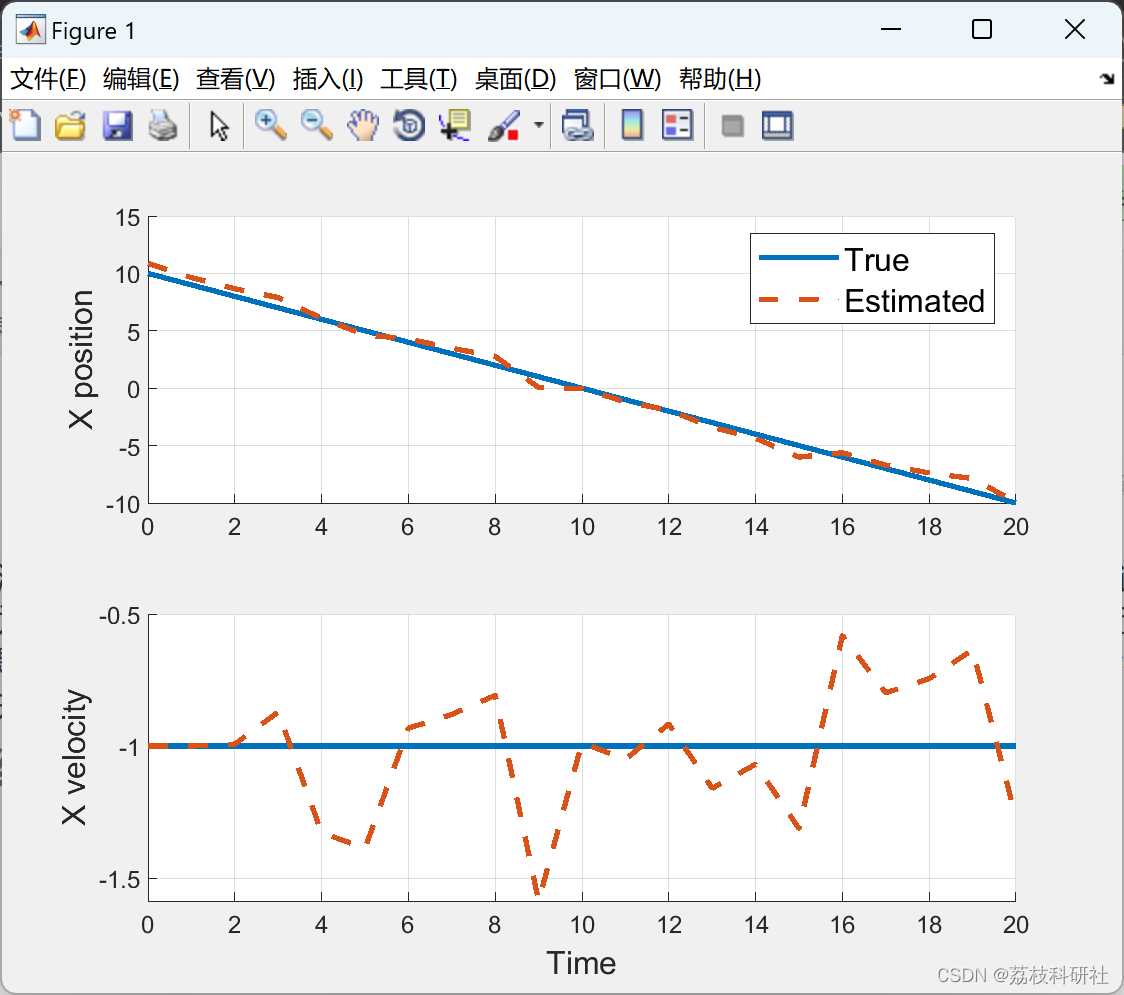
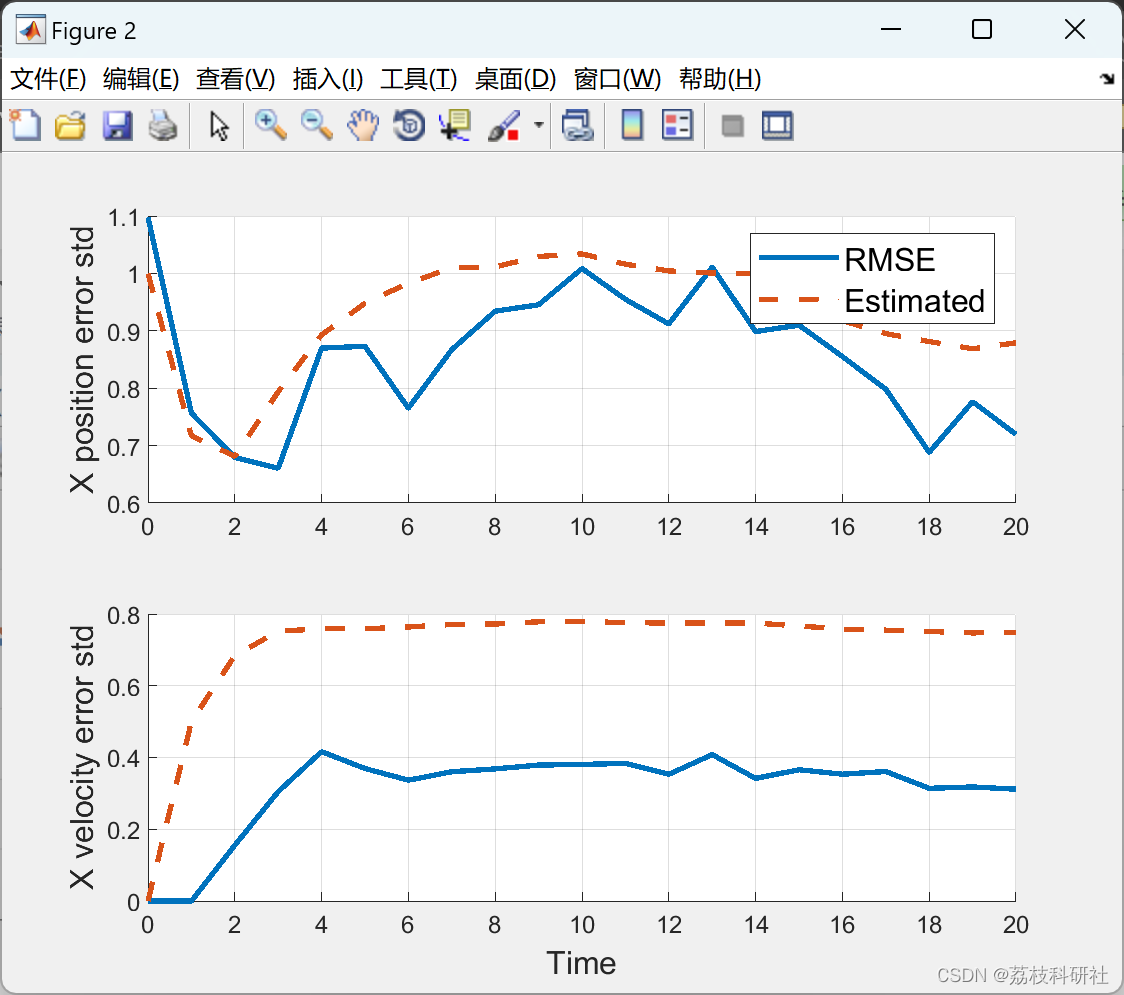
部分代码：

N = 20; % number of time steps
dt = 1; % time between time steps
M = 100; % number of Monte-Carlo runs

sig_acc_true = [0.3; 0.3; 0.3]; % true value of standard deviation of accelerometer noise
sig_gps_true = [3; 3; 3; 0.03; 0.03; 0.03]; % true value of standard deviation of GPS noise

sig_acc = [0.3; 0.3; 0.3]; % user input of standard deviation of accelerometer noise
sig_gps = [3; 3; 3; 0.03; 0.03; 0.03]; % user input of standard deviation of GPS noise

Q = [diag(0.25*dt^4*sig_acc.^2), zeros(3); zeros(3), diag(dt^2*sig_acc.^2)]; % process noise covariance matrix
R = [diag(sig_gps(1:3).^2), zeros(3); zeros(3), diag(sig_gps(4:6).^2)]; % measurement noise covariance matrix

F = [eye(3), eye(3)*dt; zeros(3), eye(3)]; % state transition matrix
B = [0.5*eye(3)*dt^2; eye(3)*dt]; % control-input matrix
H = eye(6); % measurement matrix

%% true trajectory

x_true = zeros(6,N+1); % true state
a_true = zeros(3,N);   % true acceleration

x_true(:,1) = [0; 0; 0; 5; 5; 0]; % initial true state
for k = 2:1:N+1
    x_true(:,k) = F*x_true(:,k-1) + B*a_true(:,k-1);
end

%% Kalman filter simulation

res_x_est = zeros(6,N+1,M); % Monte-Carlo estimates
res_x_err = zeros(6,N+1,M); % Monte-Carlo estimate errors
P_diag = zeros(6,N+1); % diagonal term of error covariance matrix

% filtering
for m = 1:1:M
    % initial guess
    x_est(:,1) = [2; -2; 0; 5; 5.1; 0.1];
    P = [eye(3)*4^2, zeros(3); zeros(3), eye(3)*0.4^2];
    P_diag(:,1) = diag(P);
    for k = 2:1:N+1
        
        %%% Prediction
        % obtain acceleration output
        u = a_true(:,k-1) + normrnd(0, sig_acc_true);
        
        % predicted state estimate
        x_est(:,k) = F*x_est(:,k-1) + B*u;
        
        % predicted error covariance
        P = F*P*F' + Q;
        
        %%% Update
        % obtain measurement
        z = x_true(:,k) + normrnd(0, sig_gps_true);
        
        % measurement residual

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]彭剑,刘东文.改进扩展卡尔曼滤波器的PMSM参数辨识[J].现代信息科技,2023,7(10):66-69.DOI:10.19850/j.cnki.2096-4706.2023.10.017.

[2]廖楷娴. 改进扩展卡尔曼滤波器的永磁同步风力发电机参数辨识[D].湖南工业大学,2022.DOI:10.27730/d.cnki.ghngy.2022.000263.

🌈4 Matlab代码及数据