为什么计算机对浮点型数字计算存在误差

为什么计算机对浮点型数字计算存在误差？

我们输入的十进制小数在计算机中都是以二进制进行存储。比如：

我们把0.25转换为二进制
0.25 * 2 = 0.5  取0
0.50 * 2 = 1.0  取1
所以十进制0.25的二进制应当为0.01

但是我们把0.3转换为二进制存储
0.3 * 2 = 0.6   取0
0.6 * 2 = 1.2   取1
0.2 * 2 = 0.4   取0
0.4 * 2 = 0.8   取0
0.8 * 2 = 1.6   取1
0.6 * 2 = 1.2   取1
0.2 * 2 = 0.4   取0
......
所以十进制0.3的转为二进制应当为0.01001100110011的无限循环小数。

由此可见0.3在计算机中存储的值永远小于0.3，所以当使用0.3计算时，就会产生误差。

在计算机中浮点型不能直接使用等号比较也是同一个道理。举个李子：

#include
void comp(double a, double b){
    printf("两个数:a = %g, b = %g 开始比较\n", a, b);
    if(a == b){
        printf("a equal b\n");
    }
    else{
        printf("a not equal b\n");
        printf("a - b = %g\n", a - b);
    }
}
int main(){
    comp(0.25 + 0.25 + 0.25 + 0.25, 1.0);
    comp(0.3 + 0.3, 0.6);
    comp(0.3 + 0.3 + 0.3 + 0.1, 1);
    return 0;
}

执行结果：

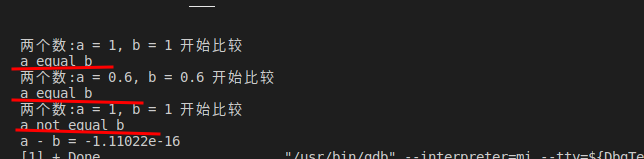
可以看出当涉及到0.3的运算超出一定的精度后，就会计算错误。

这就是为什么浮点型运算在计算机中会存在误差的原因。