并查集介绍

并查集原理

在一些应用问题中，需要将 n 个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按照一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于哪一个集合的运算。适合于描述这类问题的抽象数据类型称为并查集（union-find disjoint sets）。

并查集是一种树形的数据结构，用于处理一些不相交的集合的合并及查询问题。并查集的思想是用一个数组表示整片森林，数的根节点唯一标识了一个集合，我们只要能找到某个元素的树根，就能确定它在哪个集合里面。

例如：某校某班今年新招生10人，西安4人，成都3人，海南3人，10个人来自不同的地方，刚开始互相不认识，每个学生都是一个独立的小团体，现在给10个学生进行编号：0 - 9 号，下面我们用数组来存储该小集体，数组中的数字代表：该小集体中具有成员的个数。

到校之后，每个地方的学生自发组成一个小分队，即西安分队 s1 = {0，6，7，8}，成都分队 s2 = {1，4，9}，海南分队 s3 = {2，3，5}，10个人形成了三个小团体。假设每个小分队的第一个成员 0，1，2 担任队长。

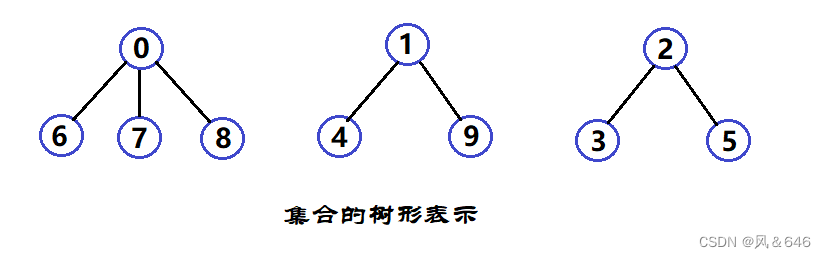
经过一段时间之后他们互相就熟悉起来了。

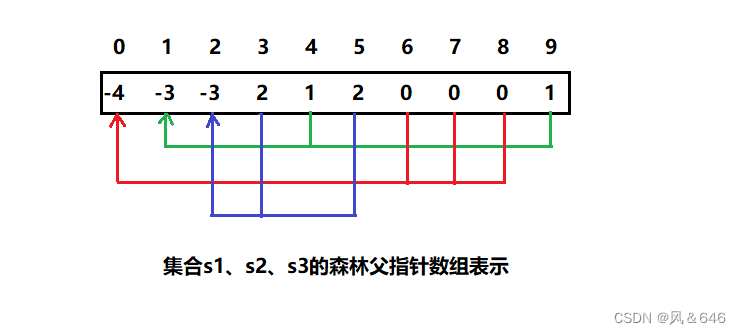
通过上面两图，可以得出以下结论：

• 数组的下标对应集合中元素的编号
• 数组中如果为负数，负号代表根，数字代表该集合中元素的个数
• 数组中如果为非负数，代表该元素的父亲在数组中的下标

来到学校学习一段时间之后，西安小分队中8号同学与成都小分队中1号同学成为了朋友，通过同学之间的相互结束，最后合并为一个小团体：

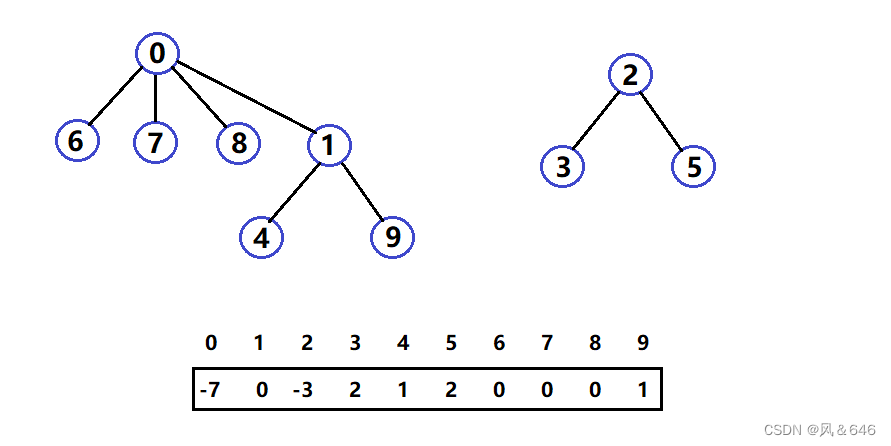
现在0集合有7个人，2集合有三个人，总共两个小团体。

通过以上，并查集一般可以解决下列问题：

1. 查找元素属于哪个集合（沿着数组表示树形关系往上一直找到根，即树中元素为负数的位置）。
2. 查看两个元素是否属于同一个集合（沿着数组表示的树形关系一直往上找到树的个，若两个元素根在同一个集合，那么就在一个集合，否则不在一个集合）。
3. 将两个集合合并为一个集合（将两个集合中的元素合并，让其中一个集合的名称改为另外一个集合的名称）。
4. 统计集合的个数（遍历数组，统计数组中元素为负数的个数即为集合的个数）。

并查集实现

并查集的类结构

并查集的底层结构使用 vector 实现，在初始化的时候，将 vector 中的每个位置的值置为 -1。便于统计每个小集合中元素的个数。

class UnionFindSet
{
public:
	// 初始化时，将数组中元素全部设置为-1
	UnionFindSet(size_t n)
		:_ufs(n, -1)
	{}


private:
	vector<int> _ufs;
};
1
2
3
4
5
6
7
8
9
10
11
12

并查集的合并

并查集合并的步骤：

• 找到待合并的两个元素的根的下标。
• 判断它们是否已经在同一个集合，若不在同一集合，则进行以下步骤。
• 将数据量小的集合往数据量大的集合合并，然后合并两个集合元素，小的集合名称改为大的集合名称。

在每一次查找下标的时候，顺便进行路径压缩。避免路径过长造成效率损失。具体怎么做可以详细看看代码：

// 给一个元素的编号，找到该元素所在集合的名称
int FindRoot(int index)
{
	// 如果数组中存储的是负数，则找到，否则一直继续查找
	int root = index;
	while (_ufs[root] >= 0)
	{
		root = _ufs[root];
	}

	// 路径压缩
	while (_ufs[index] > 0)
	{
		int parent = _ufs[index];
		_ufs[index] = root;
		index = parent;
	}

	return root;
}

void Union(int x1, int x2)
{
	int root1 = FindRoot(x1);
	int root2 = FindRoot(x2);

	// 如果root1==root2，本身就在一个集合，就没有必要合并了
	if (root1 == root2)
		return;

	// 若没有在一个集合，则数据量小的集合往数据量大的集合合并
	if (abs(_ufs[root1]) < abs(_ufs[root2]))
		swap(root1, root2);

	// 将两个集合中元素合并
	_ufs[root1] += _ufs[root2];
	// 将其中一个集合的名称改为另外一个
	_ufs[root2] = root1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

统计集合数量

// 统计集合的个数，数组中负数的个数，即为集合的个数
size_t Size()const
{
	size_t count = 0;
	for (auto e : _ufs)
	{
		if (e < 0)
			++count;
	}
	return count;
}
1
2
3
4
5
6
7
8
9
10
11