-
C++查找实验
1.顺序查找
运行结果如图所示：
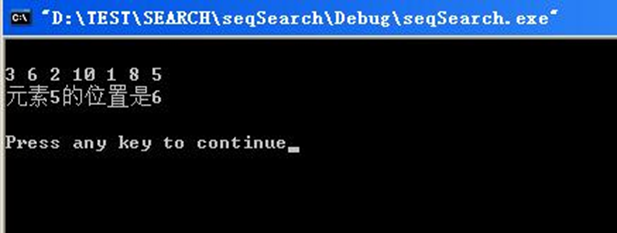
seqSearch.cpp#include//定义表中最多记录个数 #define MAXL 100 typedef int KeyType; typedef char InfoType[10]; typedef struct { //KeyType为关键字的数据类型 KeyType key; //其他数据 InfoType data; } NodeType; //顺序表类型 typedef NodeType SeqList[MAXL]; //顺序查找算法 int SeqSearch(SeqList R, int n, KeyType k) { int index = 0; for (int i = 0; i < n; i++) { if (R[i].key == k) { index = i; } printf("%d ", R[i].key); } return index; } int main() { SeqList R; int n = 10; KeyType k = 5; int a[] = {3, 6, 2, 10, 1, 8, 5, 7, 4, 9}; int i; //建立顺序表 for (i = 0; i < n; i++) { R[i].key = a[i]; } printf("\n"); if ((i = SeqSearch(R, n, k)) != -1) { printf("\n元素%d的位置是%d\n", k, i); } else { printf("\n元素%d不在表中\n", k); } printf("\n"); } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
运行截图
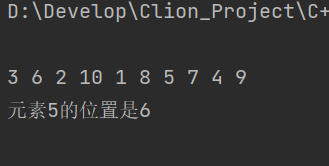
2. 折半查找
运行结果如图所示：
binSearch.cpp#include//定义表中最多记录个数 #define MAXL 100 typedef int KeyType; typedef char InfoType[10]; typedef struct { //KeyType为关键字的数据类型 KeyType key; //其他数据 InfoType data; } NodeType; //顺序表类型 typedef NodeType SeqList[MAXL]; //二分查找算法 int BinSearch(SeqList R, int n, KeyType k) { int low = 1; int high = n; int count = 1; int res = 0; while (low <= high && count < 4) { int mid = (low + high) / 2; if (count < 3) { printf("第%d次查找:在[%d,%d]中查找到元素R[%d]:%d\n", count, low - 1, high - 1, mid - 1, R[mid - 1].key); } if (k == R[mid].key) { res = mid; high = n; low = R[mid].key; count++; printf("第%d次查找:在[%d,%d]中查找到元素R[%d]:%d\n", count, low - 1, high - 1, res, R[res].key); } else if (k < R[mid].key) { high = mid - 1; } else { low = mid + 1; } count++; } return res; } int main() { SeqList R; KeyType k = 9; int a[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, i, n = 10; //建立顺序表 for (i = 0; i < n; i++) { R[i].key = a[i]; } printf("\n"); if ((i = BinSearch(R, n, k)) != -1) { printf("元素%d的位置是%d\n", k, i); } else { printf("元素%d不在表中\n", k); } printf("\n"); } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
运行截图
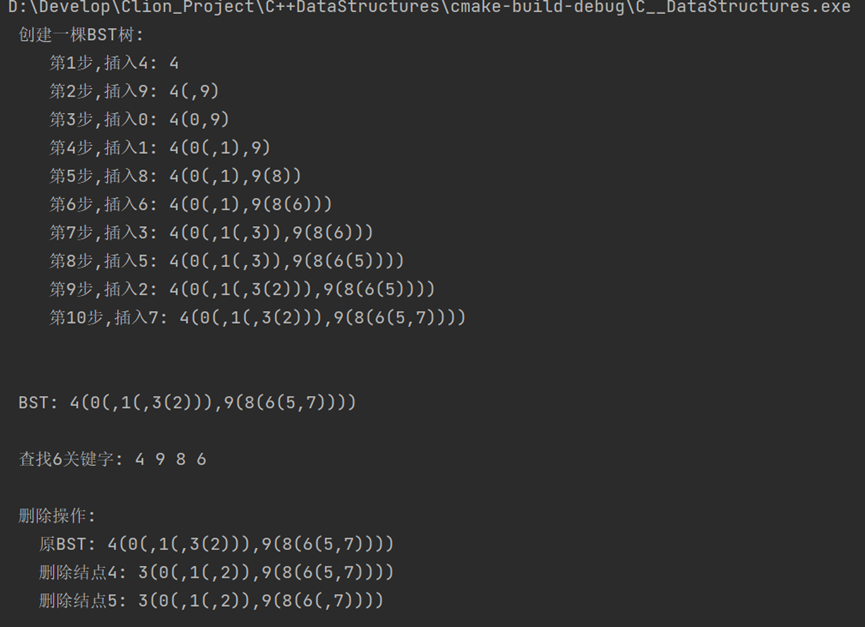
3. 二叉排序树的基本运算
运行结果如图所示：
BST.cpp#include#include #define MaxSize 100 //定义关键字类型 typedef int KeyType; typedef char InfoType; //记录类型 typedef struct node { //关键字项 KeyType key; //其他数据域 InfoType data; //左右孩子指针 struct node *lchild; struct node *rchild; } BSTNode; //全局变量,用于存放路径 int path[MaxSize]; //函数说明 void DispBST(BSTNode *b); //在以*p为根结点的BST中插入一个关键字为k的结点 int InsertBST(BSTNode *&p, KeyType k) { //原树为空, 新插入的记录为根结点 if (p == nullptr) { p = (BSTNode *) malloc(sizeof(BSTNode)); p->key = k; p->lchild = p->rchild = nullptr; return 1; } else if (k == p->key) { return 0; } else if (k < p->key) { //递归调用，插入到*p的左子树中 return InsertBST(p->lchild, k); } else { //递归调用，插入到*p的右子树中 return InsertBST(p->rchild, k); } } //由数组A中的关键字建立一棵二叉排序树 BSTNode *CreatBST(KeyType A[], int n) { //初始时bt为空树 BSTNode *bt = nullptr; int i = 0; while (i < n) //将A[i]插入二叉排序树T中 if (InsertBST(bt, A[i]) == 1) { printf(" 第%d步,插入%d: ", i + 1, A[i]); DispBST(bt); printf("\n"); i++; } //返回建立的二叉排序树的根指针 return bt; } //以括号表示法输出二叉排序树bt void DispBST(BSTNode *bt) { if (bt != nullptr) { printf("%d", bt->key); if (bt->lchild != nullptr || bt->rchild != nullptr) { printf("("); DispBST(bt->lchild); if (bt->rchild != nullptr) { printf(","); } DispBST(bt->rchild); printf(")"); } } } //以递归方式输出从根结点到查找到的结点的路径 int SearchBST(BSTNode *bt, KeyType k) { printf("%d ", bt->key); if (k == bt->key) { return bt->key; } else if (k < bt->key) { return SearchBST(bt->lchild, k); } else if (k > bt->key) { return SearchBST(bt->rchild, k); } } //当被删*p结点有左右子树时的删除过程 void Delete1(BSTNode *p, BSTNode *&r) { BSTNode *s; BSTNode *q; q = p; s = p->lchild; while (s->rchild) { q = s; s = s->rchild; } p->key = s->key; if (q != p) { q->rchild = s->lchild; } else { q->lchild = s->lchild; } delete s; /* if (r->rchild != nullptr) Delete1(p, p->lchild); //递归找最右下结点 else //找到了最右下结点*r { p->key = r->key; //将*r的关键字值赋给*p q = r; r = r->lchild; //将*r的双亲结点的右孩子结点改为*r的左孩子结点 free(q); //释放原*r的空间 } */ } //从二叉排序树中删除*p结点 void Delete(BSTNode *&p) { BSTNode *q; //*p结点没有右子树的情况 if (p->rchild == nullptr) { q = p; p = p->lchild; free(q); } else if (p->lchild == nullptr) { //*p结点没有左子树的情况 q = p; p = p->rchild; free(q); } else { //*p结点既有左子树又有右子树的情况 Delete1(p, p->lchild); } } //在bt中删除关键字为k的结点 int DeleteBST(BSTNode *&bt, KeyType k) { //空树删除失败 if (bt == nullptr) { return 0; } else { //小于说明在左边 if (k < bt->key) { //递归在左子树中删除关键字为k的结点 return DeleteBST(bt->lchild, k); } else if (k > bt->key) { //递归在右子树中删除关键字为k的结点 return DeleteBST(bt->rchild, k); } else { //k=bt->key的情况 //调用Delete(bt)函数删除*bt结点 Delete(bt); return 1; } } } int flag = true; int prev=-256; bool isBinaryTree(BSTNode *&bt) { if (bt->lchild != nullptr && flag) { isBinaryTree(bt->lchild); } if(bt->data<prev){ flag= false; } if(bt->rchild!= nullptr&&flag){ isBinaryTree(bt->rchild); } return flag; } //predt为全局变量,保存当前结点中序前趋的值,初值为-∞ KeyType predt = -32767; int main() { BSTNode *bt; KeyType k = 6; int a[] = {4, 9, 0, 1, 8, 6, 3, 5, 2, 7}, n = 10; /* 4 / \ 0 9 \ / 1 8 \ / 3 6 / /\ 2 5 7 */ printf(" 创建一棵BST树:"); printf("\n"); bt = CreatBST(a, n); printf("\n\n BST: "); DispBST(bt); printf("\n\n"); printf(" 查找%d关键字: ", k); SearchBST(bt, k); printf("\n\n"); printf(" 是否是二叉排序树: \n"); if(isBinaryTree(bt)){ printf(" 是二叉排序树 \n"); } else{ printf(" 不是二叉排序树 \n"); } printf("\n\n 删除操作:\n"); printf(" 原BST: "); DispBST(bt); printf("\n"); printf(" 删除结点4: "); DeleteBST(bt, 4); DispBST(bt); printf("\n"); printf(" 删除结点5: "); DeleteBST(bt, 5); DispBST(bt); printf("\n\n"); } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
运行截图
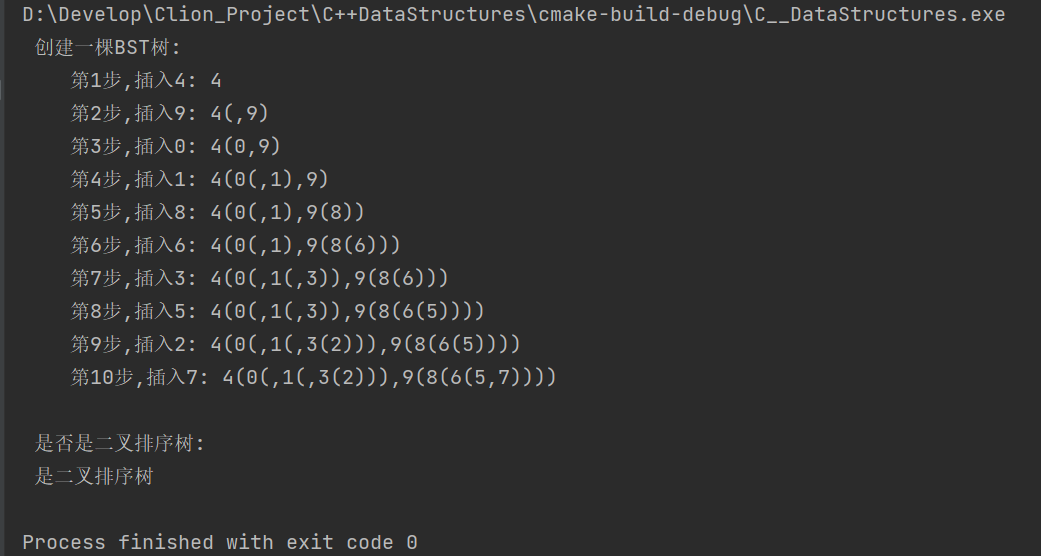
4.自行设计一个算法，判别给定的一棵二叉树是否为二叉排序树
根据第三题结构，添加如下算法代码
#include#include #define MaxSize 100 //定义关键字类型 typedef int KeyType; typedef char InfoType; //记录类型 typedef struct node { //关键字项 KeyType key; //其他数据域 InfoType data; //左右孩子指针 struct node *lchild; struct node *rchild; } BSTNode; //全局变量,用于存放路径 int path[MaxSize]; //函数说明 void DispBST(BSTNode *b); //在以*p为根结点的BST中插入一个关键字为k的结点 int InsertBST(BSTNode *&p, KeyType k) { //原树为空, 新插入的记录为根结点 if (p == nullptr) { p = (BSTNode *) malloc(sizeof(BSTNode)); p->key = k; p->lchild = p->rchild = nullptr; return 1; } else if (k == p->key) { return 0; } else if (k < p->key) { //递归调用，插入到*p的左子树中 return InsertBST(p->lchild, k); } else { //递归调用，插入到*p的右子树中 return InsertBST(p->rchild, k); } } //由数组A中的关键字建立一棵二叉排序树 BSTNode *CreatBST(KeyType A[], int n) { //初始时bt为空树 BSTNode *bt = nullptr; int i = 0; while (i < n) //将A[i]插入二叉排序树T中 if (InsertBST(bt, A[i]) == 1) { printf(" 第%d步,插入%d: ", i + 1, A[i]); DispBST(bt); printf("\n"); i++; } //返回建立的二叉排序树的根指针 return bt; } //以括号表示法输出二叉排序树bt void DispBST(BSTNode *bt) { if (bt != nullptr) { printf("%d", bt->key); if (bt->lchild != nullptr || bt->rchild != nullptr) { printf("("); DispBST(bt->lchild); if (bt->rchild != nullptr) { printf(","); } DispBST(bt->rchild); printf(")"); } } } int flag = true; int prev=-256; bool isBinaryTree(BSTNode *&bt) { if (bt->lchild != nullptr && flag) { isBinaryTree(bt->lchild); } if(bt->data<prev){ flag= false; } if(bt->rchild!= nullptr&&flag){ isBinaryTree(bt->rchild); } return flag; } //predt为全局变量,保存当前结点中序前趋的值,初值为-∞ KeyType predt = -32767; int main() { BSTNode *bt; KeyType k = 6; int a[] = {4, 9, 0, 1, 8, 6, 3, 5, 2, 7}, n = 10; /* 4 / \ 0 9 \ / 1 8 \ / 3 6 / /\ 2 5 7 */ printf(" 创建一棵BST树:"); printf("\n"); bt = CreatBST(a, n); printf("\n"); printf(" 是否是二叉排序树: \n"); if(isBinaryTree(bt)){ printf(" 是二叉排序树 \n"); } else{ printf(" 不是二叉排序树 \n"); } } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
运行截图
-
相关阅读:
相控阵天线有源驻波测试
【2022黑马程序员】SQL优化
FPGA实现电机霍尔编码器模块
研发效能之环境管理
ts学习02-数据类型
力扣336.回文对 ——字符串哈希
java 同学聚会AA制共享账单系统springboot 小程序022
自动控制原理8.5---非线性控制的逆系统方法
机器人控制器编程实践指导书旧版-实践一 LED灯（数字量）
sql 注入(2), 文件读写 木马植入 远程控制
- 原文地址：https://blog.csdn.net/qq_51495235/article/details/128155891
