-
Improper integral
In mathematical analysis, an improper integral is the limit of a definite integral as an endpoint of the interval(s) of integration approaches either a specified real number or positive or negative infinity; or in some instances as both endpoints approach limits. Such an integral is often written symbolically just like a standard definite integral, in some cases with infinity as a limit of integration.
Specifically, an improper integral is a limit of the form:
{\displaystyle \lim _{b\to \infty }\int _{a}^{b}f(x),dx,\quad \lim _{a\to -\infty }\int _{a}^{b}f(x),dx}{\displaystyle \lim _{b\to \infty }\int _{a}^{b}f(x),dx,\quad \lim _{a\to -\infty }\int _{a}^{b}f(x),dx}
or{\displaystyle \lim _{c\to b^{-}}\int _{a}^{c}f(x)\ dx,\quad \lim _{c\to a^{+}}\int _{c}^{b}f(x)\ dx}{\displaystyle \lim _{c\to b^{-}}\int _{a}^{c}f(x)\ dx,\quad \lim _{c\to a^{+}}\int _{c}^{b}f(x)\ dx}
in which one takes a limit in one or the other (or sometimes both) endpoints (Apostol 1967, §10.23).By abuse of notation, improper integrals are often written symbolically just like standard definite integrals, perhaps with infinity among the limits of integration. When the definite integral exists (in the sense of either the Riemann integral or the more powerful Lebesgue integral), this ambiguity is resolved as both the proper and improper integral will coincide in value.
Often one is able to compute values for improper integrals, even when the function is not integrable in the conventional sense (as a Riemann integral, for instance) because of a singularity in the function or because one of the bounds of integration is infinite.
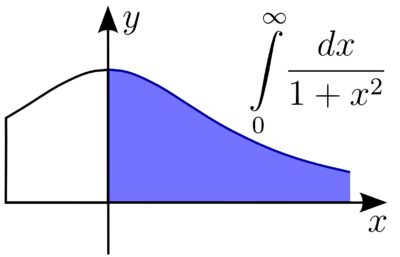
An improper integral of the first kind. The integral may need to be defined on an unbounded domain.
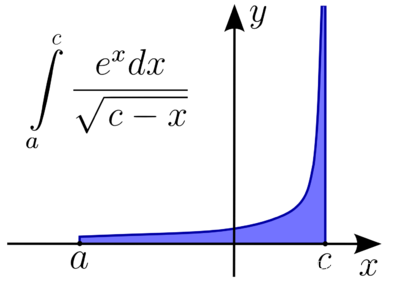
An improper Riemann integral of the second kind. The integral may fail to exist because of a vertical asymptote in the function.
Contents
1 Examples
The original definition of the Riemann integral does not apply to a function such as {\displaystyle 1/{x{2}}}1/{x{2}} on the interval [1, ∞), because in this case the domain of integration is unbounded. However, the Riemann integral can often be extended by continuity, by defining the improper integral instead as a limit
{\displaystyle \int _{1}^{\infty }{\frac {dx}{x^{2}}}=\lim _{b\to \infty }\int _{1}^{b}{\frac {dx}{x^{2}}}=\lim _{b\to \infty }\left(-{\frac {1}{b}}+{\frac {1}{1}}\right)=1.}{\displaystyle \int _{1}^{\infty }{\frac {dx}{x^{2}}}=\lim _{b\to \infty }\int _{1}^{b}{\frac {dx}{x^{2}}}=\lim _{b\to \infty }\left(-{\frac {1}{b}}+{\frac {1}{1}}\right)=1.}
The narrow definition of the Riemann integral also does not cover the function {\textstyle 1/{\sqrt {x}}}{\textstyle 1/{\sqrt {x}}} on the interval [0, 1]. The problem here is that the integrand is unbounded in the domain of integration (the definition requires that both the domain of integration and the integrand be bounded). However, the improper integral does exist if understood as the limit{\displaystyle \int _{0}^{1}{\frac {dx}{\sqrt {x}}}=\lim _{a\to 0^{+}}\int _{a}^{1}{\frac {dx}{\sqrt {x}}}=\lim _{a\to 0^{+}}\left(2-2{\sqrt {a}}\right)=2.}{\displaystyle \int _{0}^{1}{\frac {dx}{\sqrt {x}}}=\lim _{a\to 0^{+}}\int _{a}^{1}{\frac {dx}{\sqrt {x}}}=\lim _{a\to 0^{+}}\left(2-2{\sqrt {a}}\right)=2.}
Sometimes integrals may have two singularities where they are improper. Consider, for example, the function 1/((x + 1)√x) integrated from 0 to ∞ (shown right). At the lower bound, as x goes to 0 the function goes to ∞, and the upper bound is itself ∞, though the function goes to 0. Thus this is a doubly improper integral. Integrated, say, from 1 to 3, an ordinary Riemann sum suffices to produce a result of π/6. To integrate from 1 to ∞, a Riemann sum is not possible. However, any finite upper bound, say t (with t > 1), gives a well-defined result, 2 arctan(√t) − π/2. This has a finite limit as t goes to infinity, namely π/2. Similarly, the integral from 1/3 to 1 allows a Riemann sum as well, coincidentally again producing π/6. Replacing 1/3 by an arbitrary positive value s (with s < 1) is equally safe, giving π/2 − 2 arctan(√s). This, too, has a finite limit as s goes to zero, namely π/2. Combining the limits of the two fragments, the result of this improper integral is
{\displaystyle {
}}{\displaystyle {∫ 0 ∞ d x ( 1 + x ) x = lim s → 0 + ∫ s 1 d x ( 1 + x ) x + lim t → ∞ ∫ 1 t d x ( 1 + x ) x & = lim s → 0 + ( π 2 − 2 arctan s ) + lim t → ∞ ( 2 arctan t − π 2 ) & = π 2 + ( π − π 2 ) & = π . }}∫ 0 ∞ d x ( 1 + x ) x = lim s → 0 + ∫ s 1 d x ( 1 + x ) x + lim t → ∞ ∫ 1 t d x ( 1 + x ) x & = lim s → 0 + ( π 2 − 2 arctan s ) + lim t → ∞ ( 2 arctan t − π 2 ) & = π 2 + ( π − π 2 ) & = π .
This process does not guarantee success; a limit might fail to exist, or might be infinite. For example, over the bounded interval from 0 to 1 the integral of 1/x does not converge; and over the unbounded interval from 1 to ∞ the integral of 1/√x does not converge.It might also happen that an integrand is unbounded near an interior point, in which case the integral must be split at that point. For the integral as a whole to converge, the limit integrals on both sides must exist and must be bounded. For example:
{\displaystyle {
}}{\displaystyle {∫ − 1 1 d x x 2 3 = lim s → 0 − ∫ − 1 s d x x 2 3 + lim t → 0 + ∫ t 1 d x x 2 3 & = lim s → 0 − 3 ( 1 − s 3 ) + lim t → 0 + 3 ( 1 − t 3 ) & = 3 + 3 & = 6. }}∫ − 1 1 d x x 2 3 = lim s → 0 − ∫ − 1 s d x x 2 3 + lim t → 0 + ∫ t 1 d x x 2 3 & = lim s → 0 − 3 ( 1 − s 3 ) + lim t → 0 + 3 ( 1 − t 3 ) & = 3 + 3 & = 6.
But the similar integral{\displaystyle \int _{-1}^{1}{\frac {dx}{x}}}{\displaystyle \int _{-1}^{1}{\frac {dx}{x}}}
cannot be assigned a value in this way, as the integrals above and below zero do not independently converge. (However, see Cauchy principal value.)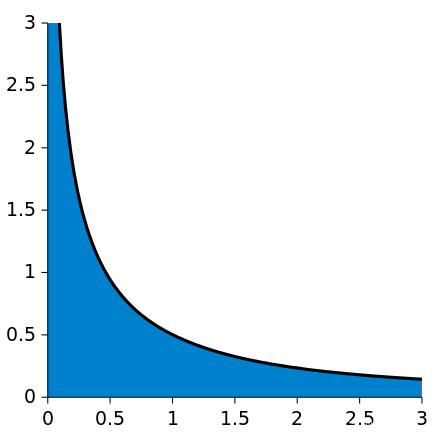
The improper integral
{\displaystyle \int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi }\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi
has unbounded intervals for both domain and range.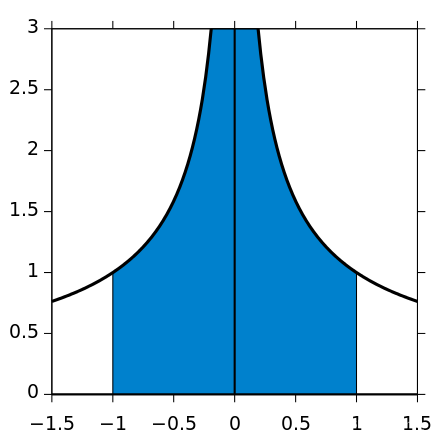
The improper integral
{\displaystyle \int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}=6}\int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}=6
converges, since both left and right limits exist, though the integrand is unbounded near an interior point.2 Convergence of the integral
An improper integral converges if the limit defining it exists. Thus for example one says that the improper integral
{\displaystyle \lim _{t\to \infty }\int _{a}^{t}f(x)\ dx}{\displaystyle \lim _{t\to \infty }\int _{a}^{t}f(x)\ dx}
exists and is equal to L if the integrals under the limit exist for all sufficiently large t, and the value of the limit is equal to L.It is also possible for an improper integral to diverge to infinity. In that case, one may assign the value of ∞ (or −∞) to the integral. For instance
{\displaystyle \lim _{b\to \infty }\int _{1}^{b}{\frac {dx}{x}}=\infty .}{\displaystyle \lim _{b\to \infty }\int _{1}^{b}{\frac {dx}{x}}=\infty .}
However, other improper integrals may simply diverge in no particular direction, such as{\displaystyle \lim _{b\to \infty }\int _{1}^{b}x\sin(x),dx,}{\displaystyle \lim _{b\to \infty }\int _{1}^{b}x\sin(x),dx,}
which does not exist, even as an extended real number. This is called divergence by oscillation.A limitation of the technique of improper integration is that the limit must be taken with respect to one endpoint at a time. Thus, for instance, an improper integral of the form
{\displaystyle \int _{-\infty }^{\infty }f(x),dx}{\displaystyle \int _{-\infty }^{\infty }f(x),dx}
can be defined by taking two separate limits; to wit{\displaystyle \int _{-\infty }^{\infty }f(x),dx=\lim _{a\to -\infty }\lim _{b\to \infty }\int _{a}^{b}f(x),dx}{\displaystyle \int _{-\infty }^{\infty }f(x),dx=\lim _{a\to -\infty }\lim _{b\to \infty }\int _{a}^{b}f(x),dx}
provided the double limit is finite. It can also be defined as a pair of distinct improper integrals of the first kind:{\displaystyle \lim _{a\to -\infty }\int _{a}^{c}f(x),dx+\lim _{b\to \infty }\int _{c}^{b}f(x),dx}{\displaystyle \lim _{a\to -\infty }\int _{a}^{c}f(x),dx+\lim _{b\to \infty }\int _{c}^{b}f(x),dx}
where c is any convenient point at which to start the integration. This definition also applies when one of these integrals is infinite, or both if they have the same sign.An example of an improper integral where both endpoints are infinite is the Gaussian integral {\textstyle \int _{-\infty }^{\infty }e{-x{2}},dx={\sqrt {\pi }}}{\textstyle \int _{-\infty }^{\infty }e{-x{2}},dx={\sqrt {\pi }}}. An example which evaluates to infinity is {\textstyle \int _{-\infty }^{\infty }e^{x},dx}{\textstyle \int _{-\infty }^{\infty }e^{x},dx}. But one cannot even define other integrals of this kind unambiguously, such as {\textstyle \int _{-\infty }^{\infty }x,dx}{\textstyle \int _{-\infty }^{\infty }x,dx}, since the double limit is infinite and the two-integral method
{\displaystyle \lim _{a\to -\infty }\int _{a}^{c}x,dx+\lim _{b\to \infty }\int _{c}^{b}x,dx}{\displaystyle \lim _{a\to -\infty }\int _{a}^{c}x,dx+\lim _{b\to \infty }\int _{c}^{b}x,dx}
yields {\displaystyle \infty -\infty }\infty -\infty . In this case, one can however define an improper integral in the sense of Cauchy principal value:{\displaystyle \operatorname {p.v.} \int _{-\infty }^{\infty }x,dx=\lim _{b\to \infty }\int _{-b}^{b}x,dx=0.}{\displaystyle \operatorname {p.v.} \int _{-\infty }^{\infty }x,dx=\lim _{b\to \infty }\int _{-b}^{b}x,dx=0.}
The questions one must address in determining an improper integral are:Does the limit exist?
Can the limit be computed?
The first question is an issue of mathematical analysis. The second one can be addressed by calculus techniques, but also in some cases by contour integration, Fourier transforms and other more advanced methods.3 Types of integrals
4 Improper Riemann integrals and Lebesgue integrals
5 Singularities
6 Cauchy principal value
7 Summability
8 Multivariable improper integrals
8.1 Improper integrals over arbitrary domains
8.2 Improper integrals with singularities
8.3 Functions with both positive and negative values
-
相关阅读:
前端分页实现
docker用法
Facebook出手!自适应梯度打败人工调参
视觉自监督学习
Android开发使用SoundPool播放音乐
【嵌入式Linux应用开发】温湿度监控系统——多线程与温湿度的获取显示
自动计算零售数据分析指标?BI软件表示可行
webpack打包ts的配置及踩坑
读书笔记-《ON JAVA 中文版》-摘要24[第二十一章 数组]
浏览器面试题
- 原文地址:https://blog.csdn.net/qq_66485519/article/details/128193301