[LeetCode周赛复盘] 第 322 场周赛20221204

一、本周周赛总结

• 打得不好。
• T2 相向双指针。
• T3 dfs。
• T4 dfs判断二分图+暴力 bfs找深度。
  

二、 [Easy] 6253. 回环句

链接: 6253. 回环句

1. 题目描述

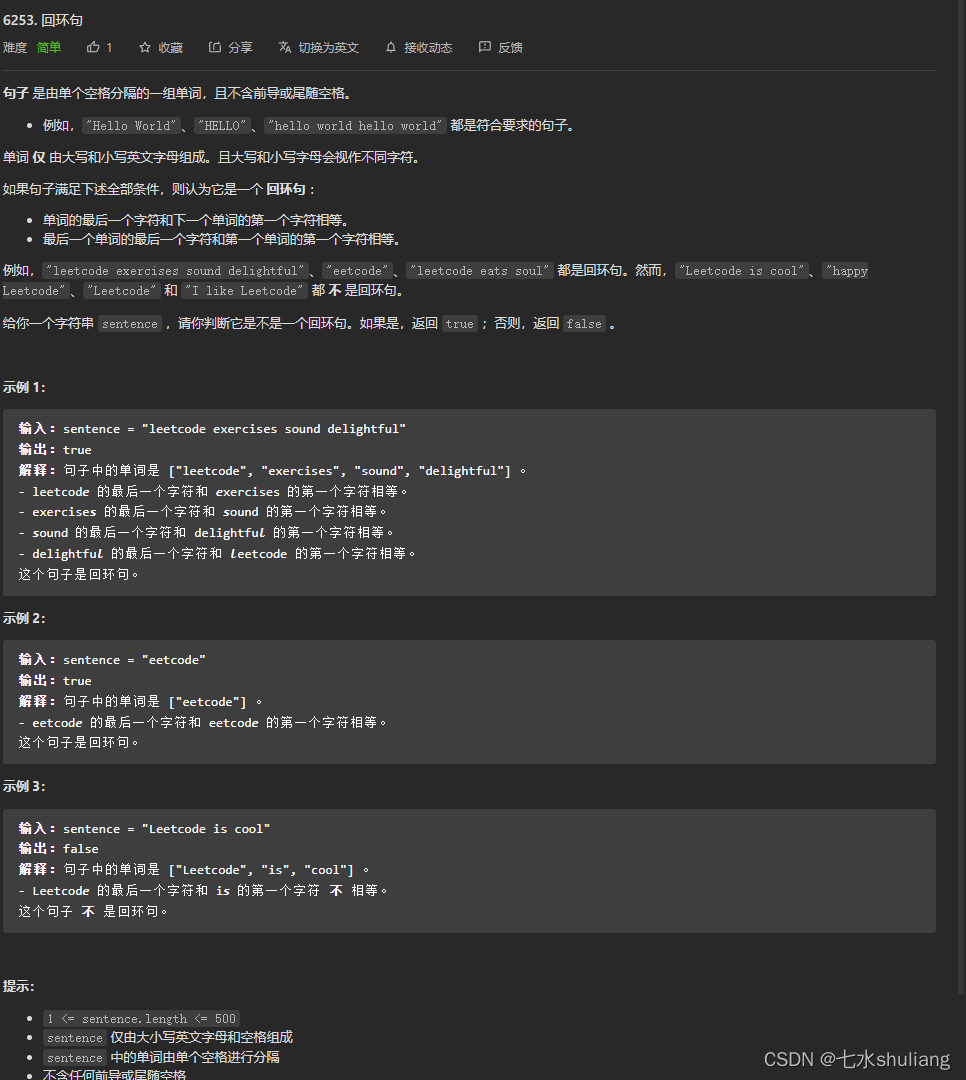
2. 思路分析

按题意模拟即可。

3. 代码实现

class Solution:
    def isCircularSentence(self, sentence: str) -> bool:
        s = sentence.split()
        if s[-1][-1] != s[0][0]:
            return False 
        for i in range(len(s)-1):
            if s[i][-1] != s[i+1][0]:
                return False
        return True
1
2
3
4
5
6
7
8
9

三、[Medium] 6254. 划分技能点相等的团队

链接: 6254. 划分技能点相等的团队

1. 题目描述

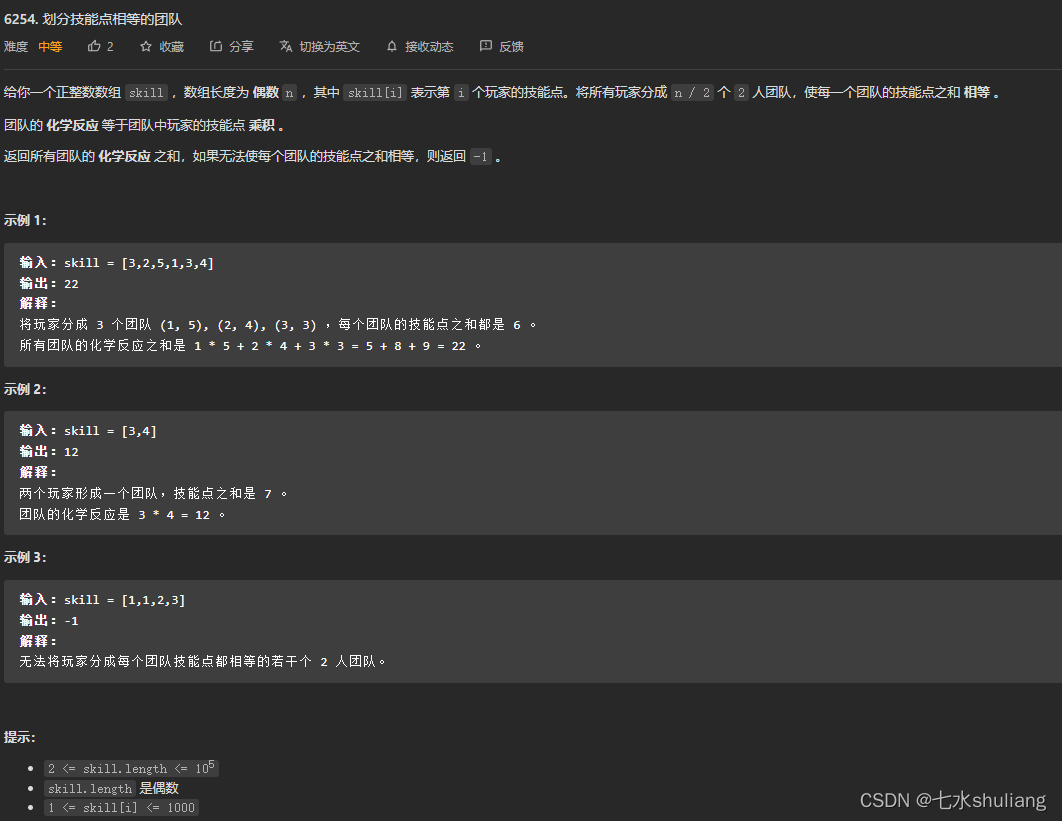
2. 思路分析

• 结论是显然的：只有大的组合小的才能平均划分。
• 因此排序后头结合尾巴即可。

3. 代码实现

class Solution:
    def dividePlayers(self, skill: List[int]) -> int:
        skill.sort()
        n = len(skill)
        l,r = 0,n-1
        s = skill[l] + skill[r]
        
        ans = 0
        while l<r:
            if skill[l] + skill[r] != s:
                return -1
            ans += skill[l]* skill[r]
            l += 1
            r -= 1
        return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

四、[Medium] 6255. 两个城市间路径的最小分数

链接: 6255. 两个城市间路径的最小分数

1. 题目描述

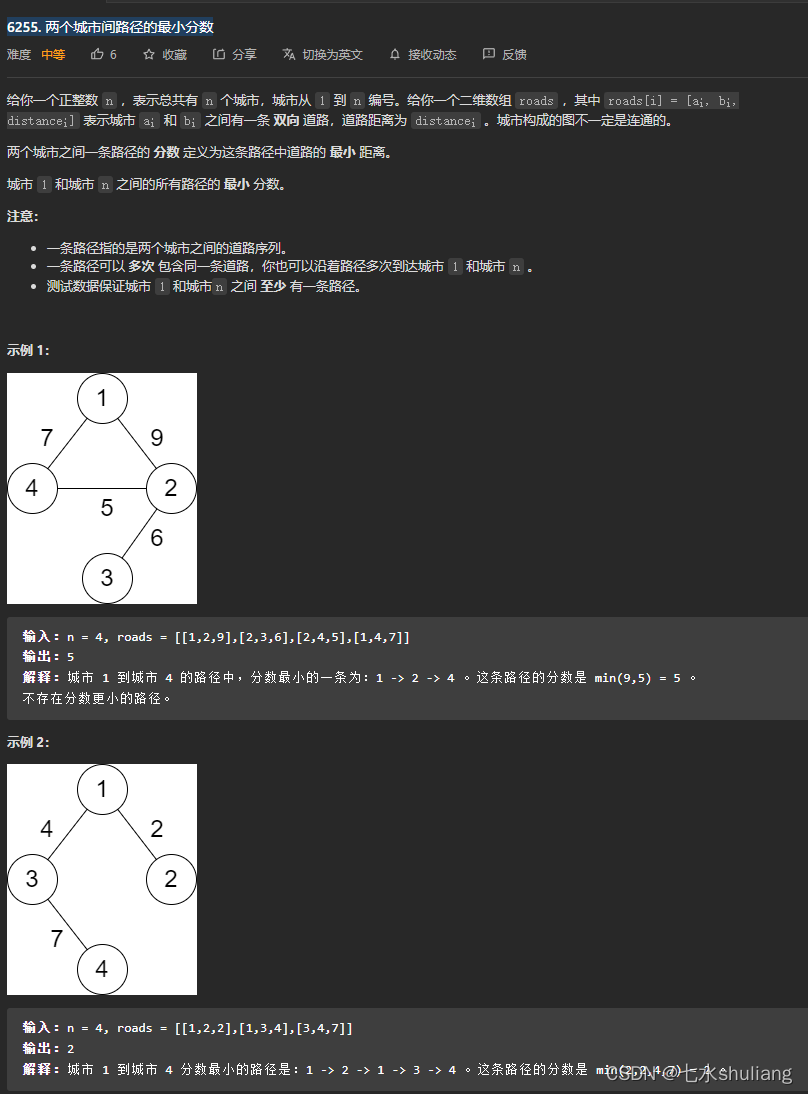
2. 思路分析

• 这题wa两次。
• 题意说的比较反常规，由于可以折返/重复走，实际是求连通1节点的所有边的最小值。
• 由于我们的vis是存的已访问的点，而不是边。因此要在vis之前更新边，因为这个边要访问下看看。

---

• 赛中我第一次wa是没提前访问边。
• 第二次tle是因为vis变成了存边，但没存双向边。

3. 代码实现

class Solution:
    def minScore(self, n: int, roads: List[List[int]]) -> int:
        g = [[] for _ in range(n)]
        for u,v,w in roads:
            u -= 1
            v -= 1
            g[u].append((v,w))
            g[v].append((u,w))
        
        vis = [0]*n 
        ans = inf
        def dfs(u):
            vis[u] = 1
            nonlocal ans
            for v,w in g[u]:
                ans = min(ans,w)
                if not vis[v]:
                    dfs(v)
        dfs(0)
        return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

五、[Hard] 6256. 将节点分成尽可能多的组

链接: 6256. 将节点分成尽可能多的组

1. 题目描述

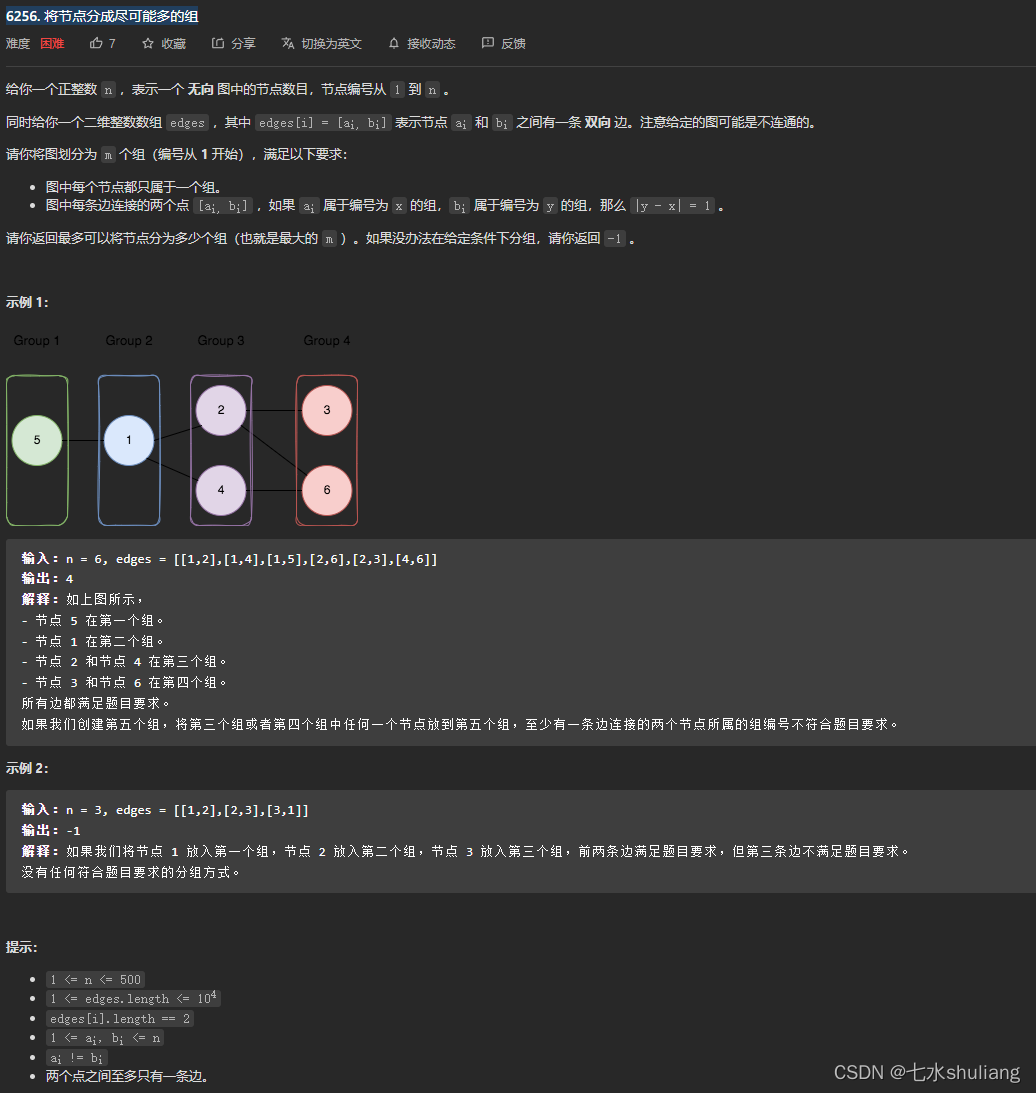
2. 思路分析

比赛时没做出来，赛后默写灵神的题解。
实际上就是两个模板，但不先找出规律，做出推论，也是想不到的。
1
2

• 手玩一下，先想树，发现树一定是有解的，因为向下延伸时分组+1即可，即层号。
• 那么图(比树多了有环)什么情况下行什么情况下不行呢，显然问题出在环上。
• 观察下，如果环长是偶数就有解，奇数则无解；因为偶数的话，从一个点往两边出发，一定可以同时到最远的点。
• 得出推论：图中有奇环，则无解；其他情况，有解。
• 没有奇环的图=二分图，因此可以用dfs染色模板判断这个图是不是二分图。
• 染色的同时给图按连通分量分组，对每个连通块里求最大层深，即：枚举每个点作为起点，求层深取max，这里其实就是n方暴力。
• 把每块的最大层深加起来，就是答案。每个连通块之间互不干扰。

3. 代码实现

class Solution:
    def magnificentSets(self, n: int, edges: List[List[int]]) -> int:
        """ 推论:   如果是树/森林，有答案
                    如果有奇环，无答案。
            没有奇环=二分图，因此
                用dfs判断是否是二分图
                用bfs枚举一个连通块中的每个点作为起点，给其它块染色最多染几组出来,即求连通块最大深度
        """
        g = [[] for _ in range(n)]
        for u,v in edges:
            g[u-1].append(v-1)
            g[v-1].append(u-1)
        
        colors = [0]*n
        def dfs(u,c):  # 判断是否是二分图
            colors[u] = c
            nodes.append(u)
            for v in g[u]:
                if colors[v] == c or not colors[v] and not dfs(v,3-c):  # 注意这个染色是标记1/2
                    return False                 
            return True

        vis = [-1]*n 
        def bfs(start):  # 以start为起点，计算这个连通分量的深度，用时间戳来优化vis，类似匈牙利的vis,这里由于每个点只会作为起点一次，所以可以用start            
            q = deque([start])
            vis[start] = start
            depth = 0
            while q:
                depth += 1
                for _ in range(len(q)):
                    u = q.popleft()
                    for v in g[u]:
                        if vis[v] != start:
                            vis[v] = start
                            q.append(v)
            return depth
                
        ans = 0        
        for i,c in enumerate(colors):  # 染色1/2是分组，0是未访问
            if not c:
                nodes = []  # 当前连通块的所有点
                if not dfs(i,1):  # 如果不是二分图，无答案
                    return -1
                ans += max(bfs(x) for x in nodes)  # 枚举一个连通块中每个起点，找最大深度
        return ans             
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

六、参考链接