wy的leetcode刷题记录_Day57

wy的leetcode刷题记录_Day57

声明

本文章的所有题目信息都来源于leetcode
如有侵权请联系我删掉!
时间：2022-12-1

前言

leetcode 每日一题+二叉树 1779. 找到最近的有相同 X 或 Y 坐标的点 701. 二叉搜索树中的插入操作

1779. 找到最近的有相同 X 或 Y 坐标的点

今天的每日一题是：1779. 找到最近的有相同 X 或 Y 坐标的点

题目介绍

给你两个整数 x 和 y ，表示你在一个笛卡尔坐标系下的 (x, y) 处。同时，在同一个坐标系下给你一个数组 points ，其中 points[i] = [ai, bi] 表示在 (ai, bi) 处有一个点。当一个点与你所在的位置有相同的 x 坐标或者相同的 y 坐标时，我们称这个点是 有效的 。

请返回距离你当前位置 曼哈顿距离 最近的 有效 点的下标（下标从 0 开始）。如果有多个最近的有效点，请返回下标 最小 的一个。如果没有有效点，请返回 -1 。

两个点 (x1, y1) 和 (x2, y2) 之间的 曼哈顿距离 为 abs(x1 - x2) + abs(y1 - y2) 。

示例 1：
输入：x = 3, y = 4, points = [[1,2],[3,1],[2,4],[2,3],[4,4]]
输出：2
解释：所有点中，[3,1]，[2,4] 和 [4,4] 是有效点。有效点中，[2,4] 和 [4,4] 距离你当前位置的曼哈顿距离最小，都为 1 。[2,4] 的下标最小，所以返回 2 。

示例 2：
输入：x = 3, y = 4, points = [[3,4]]
输出：0
提示：答案可以与你当前所在位置坐标相同。

思路

一道简单的模拟题，通过题意我们知道，我们需要寻找曼哈顿距离最小的有效点，而对于有效点的定义是x坐标或者y坐标相等，并且根据曼哈顿距离的公式我们可以知道其实距离就是x坐标或者y坐标之差（因为有一个相等了），所以我们使用俩个变量维护最短距离和最短距离下标即可。

代码

class Solution {
public:
    int nearestValidPoint(int x, int y, vector<vector<int>>& points) {
        int n=points.size();
        int min_distance=INT_MAX;
        int min_index=-1;
        for(int i=0;i<n;i++)
        {
            if(x==points[i][0])
            {
                if(min_distance>abs(y-points[i][1]))
                {
                    min_distance=abs(y-points[i][1]);
                    min_index=i;
                }

            }
            else if(y==points[i][1])
            {
                if(min_distance>abs(x-points[i][0]))
                {
                    min_distance=abs(x-points[i][0]);
                    min_index=i;
                }
            }
        }
        return min_index;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

收获

手速题。

701. 二叉搜索树中的插入操作

701. 二叉搜索树中的插入操作

题目介绍

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：

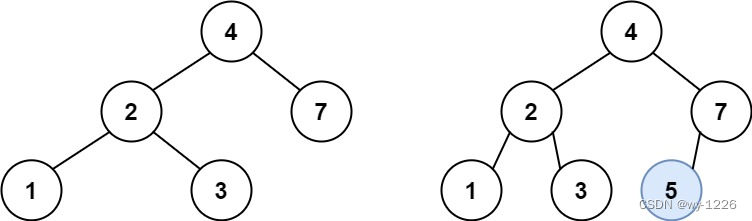
输入：root = [4,2,7,1,3], val = 5 输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

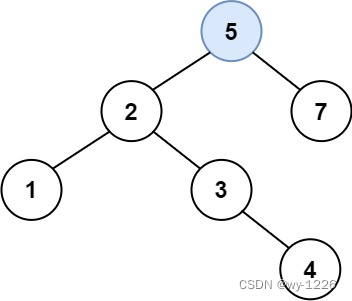
示例 2：
输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

思路

首先最简单的思路：我们忽略掉题目中的另一种插入方式：重新排列树的结构，我们只管将拆入的值加入树的叶子节点，我们可以使用递归也可以使用递推，对于递归的方法：我们首先判断需要插入的树是否为空，如果为空的话我们就以拆入的值构造根节点然后返回。如果不为空，我们判断该值与当前节点的值，如果小于当前节点的话就向左遍历，如果检查到其没有左节点后，我们插入该值构造的节点作为左节点即可，反之向右。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if(root==nullptr)
            return new TreeNode(val);
        
        if(val<root->val)
        {
            if(root->left==nullptr)
            {
                root->left=new TreeNode(val);
                return root;
            }
            root->left=insertIntoBST(root->left,val);
        }
        else
        {
            if(root->right==nullptr)
            {
                root->right=new TreeNode(val);
                return root;
            }
            root->right=insertIntoBST(root->right,val);
        }
        return root;

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

收获

巩固了搜索树的知识