单变量微积分重点（1）

1.单调有界定理

若数列递增有上界，则数列收敛（递减同样）

2.海涅定理（归结原则）

说明：对于任何的属于空心邻域的数列，而且这些数列的极限都是x0.

 3.两个重要极限：

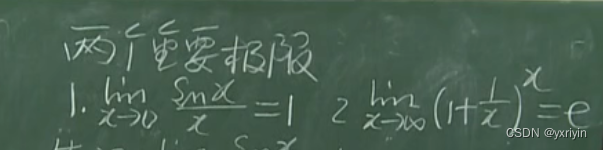
4.11个重要极限

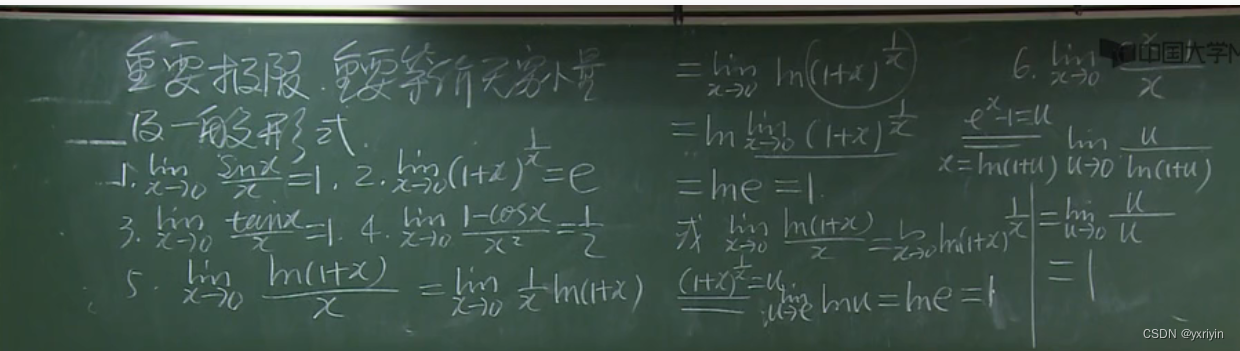
 导数定义的三种形式：

 反函数求导法则：

 证明：

函数y=f(x)存在反函数x=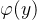,也就是说它严格单调。

所以

    

 

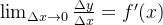
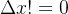
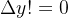
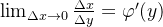
重点在于因为函数连续，所以有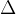x趋于0的时候有y=0

求导链式法则证明：

 

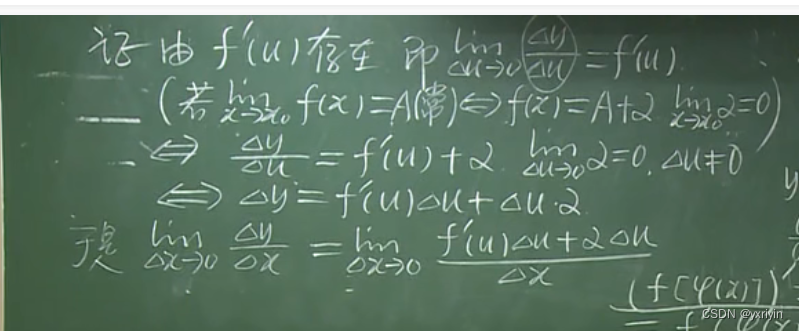
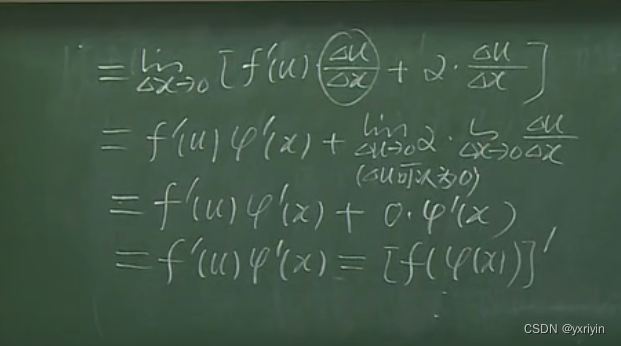
 这里主要是需要补充当u可以为0的时候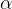=0的定义

理解下就好，证明我个人不是很感冒。

对于复合函数

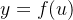
u=

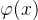
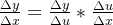
微分，自变量的增量就等于自变量的微分

 这里A和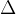x虽然无关，但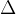x是趋于0的

对于函数y=x

dy = df(x) = dx = 1 *  

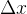
然后可以推出导数和微商：

一阶微分的形式不变性：

费马定理：

罗尔定理：

 拉格朗日定理：

 柯西定理：