二叉树的遍历与构建问题

目录

一、二叉树遍历

二、从前序与中序遍历序列构造二叉树

三、从中序遍历与后序遍历序列构造二叉树

---

一、二叉树遍历

编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

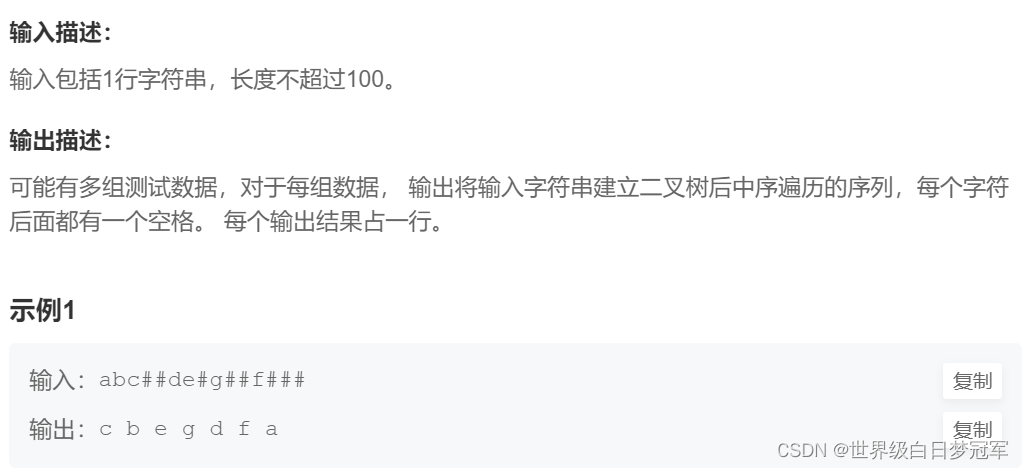
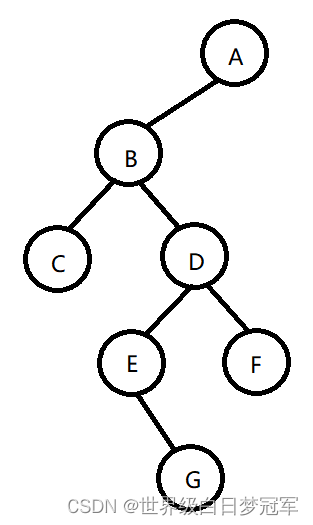
 通过实例1给定的字符串（先序遍历）能推出该树如下。它的中序遍历就是CDEGDFA。

创建两个方法，一个方法叫inorder用来中序遍历，并且输出中序遍历的结果。另一个方法叫preOrderBuild传入一个前序遍历的字符串str，就能根据前序遍历的方式构造出一颗二叉树并返回构造后的树根节点。

然后在主方法中传入一颗树的根节点按照题目要求进行输出，所有节点在一行内输出TreeNode root = preorderBuild(str);然后调用inorder(root)输出树的中序遍历，然后设置index = 0，再继续下一次的遍历使用。

在preOrderBuild方法前创建一个index变量，用它来记录传入到字符串的第几个位置，创建一个char类型的值cur来存储str在index位置上的值，当cur==‘#’，则证明该位置在树中是空的，index++然后return null即可。如下图中的第一个cur就不是#，所以创建一个TreeNode类型的root传入该值。然后将index++，root.left = preOrderBuild(s)，进入下一层递归。

 获得当前位置的将结果存储为root，然后index++，root.left = preOrderBuild(s)，进入下一层递归。

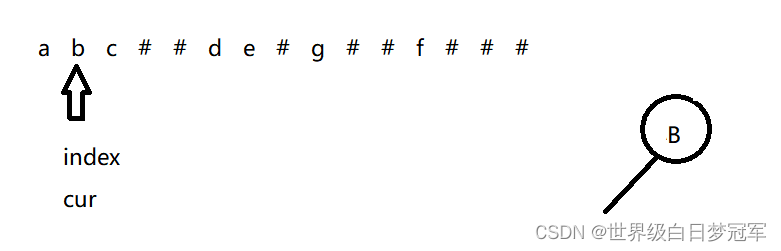
然后获得当前位置的将结果存储为root，然后index++，root.left = preOrderBuild(s)，进入下一层递归。

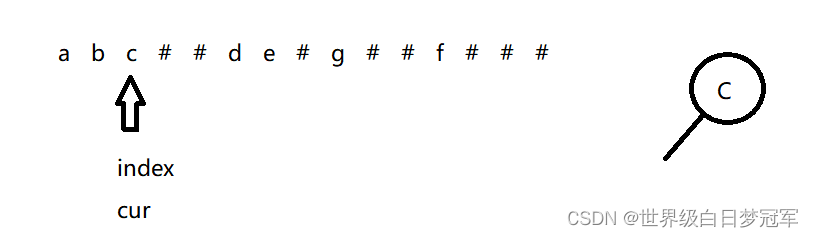
 然后就遇到了第一个#号，则直接返回null值，所以C的左子树就是空的，然后root.right = preOrderBuild(s)，进入下一层递归。

遇到了#号，返回null值，所以C的右子树也是空的，那么直接返回这颗树，那么B的左子树就是C，然后root.right = preOrderBuild(s)，继续递归。

 后面的递归图如下：

 

 

 

 

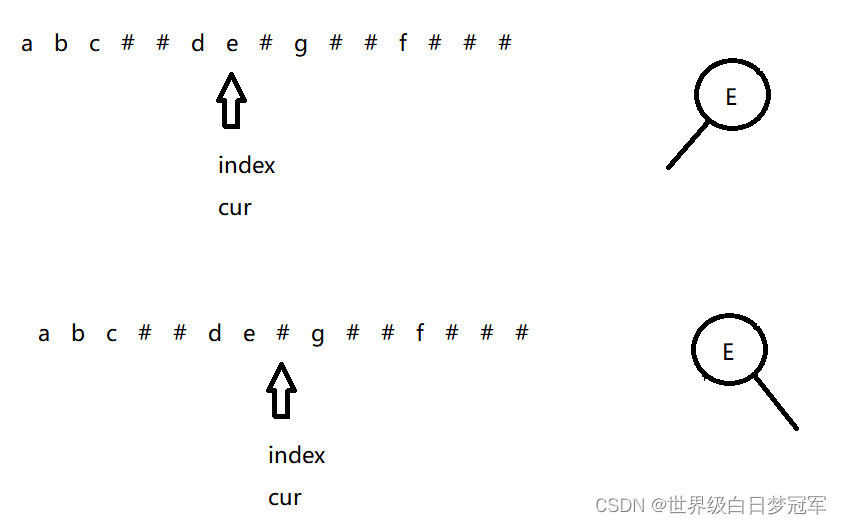
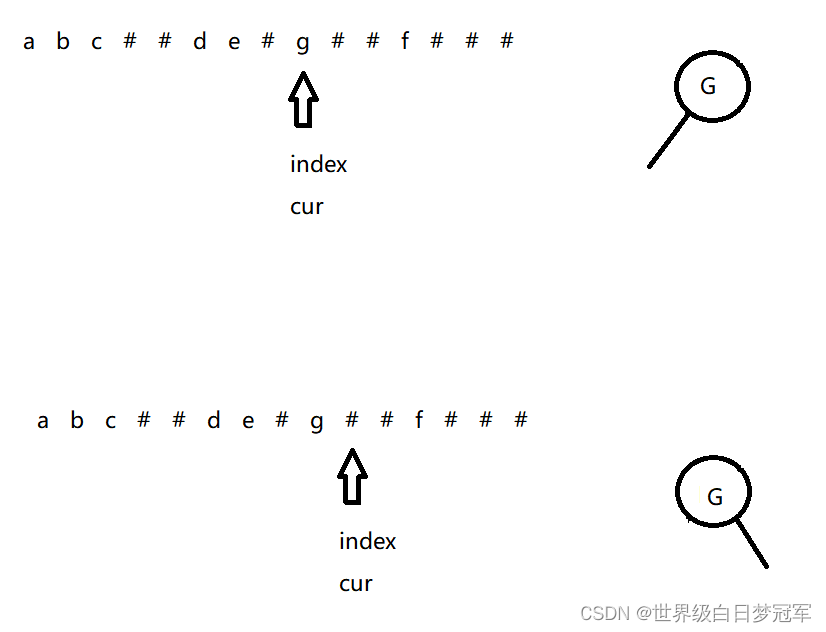
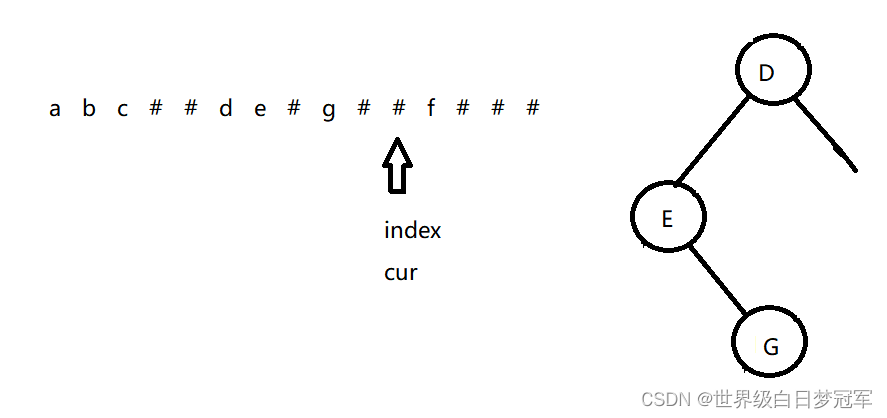
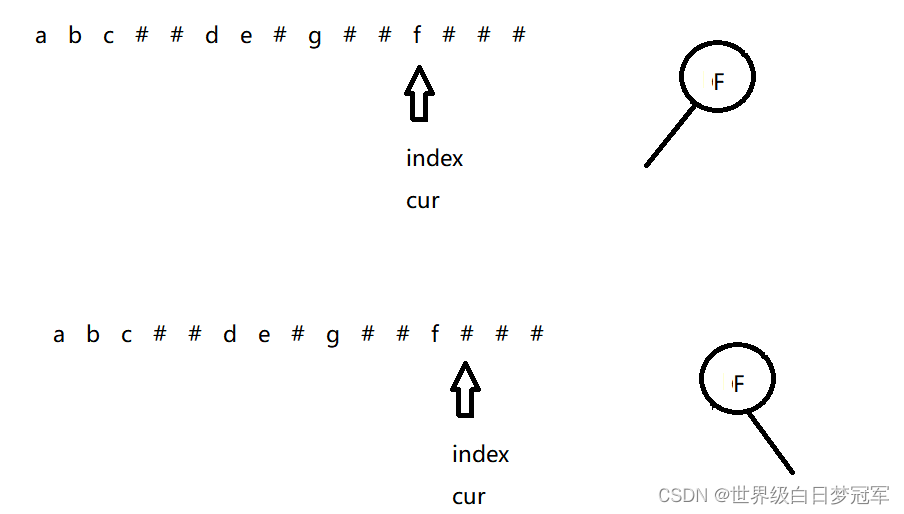
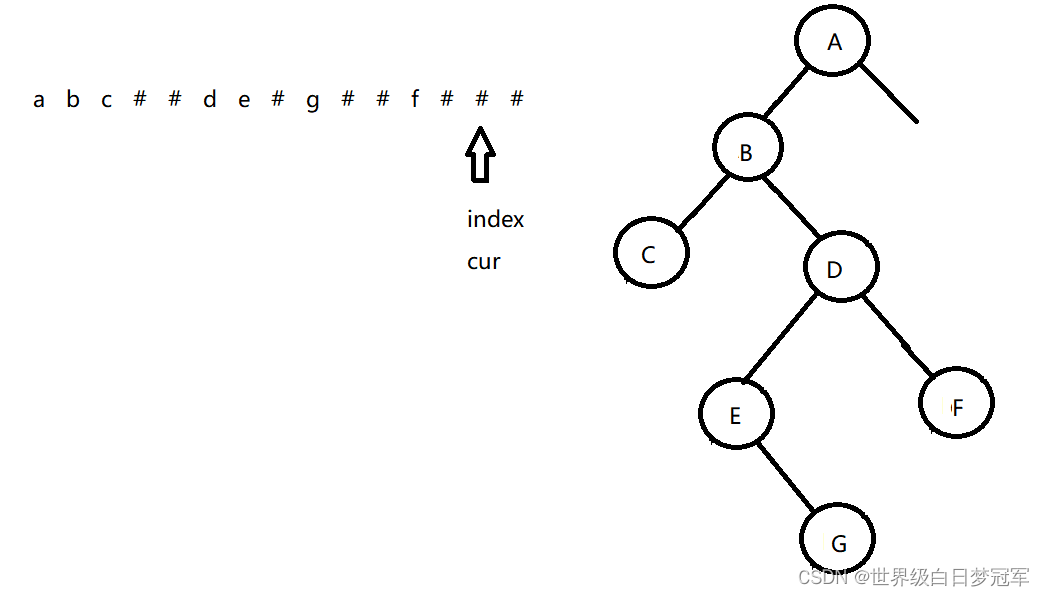
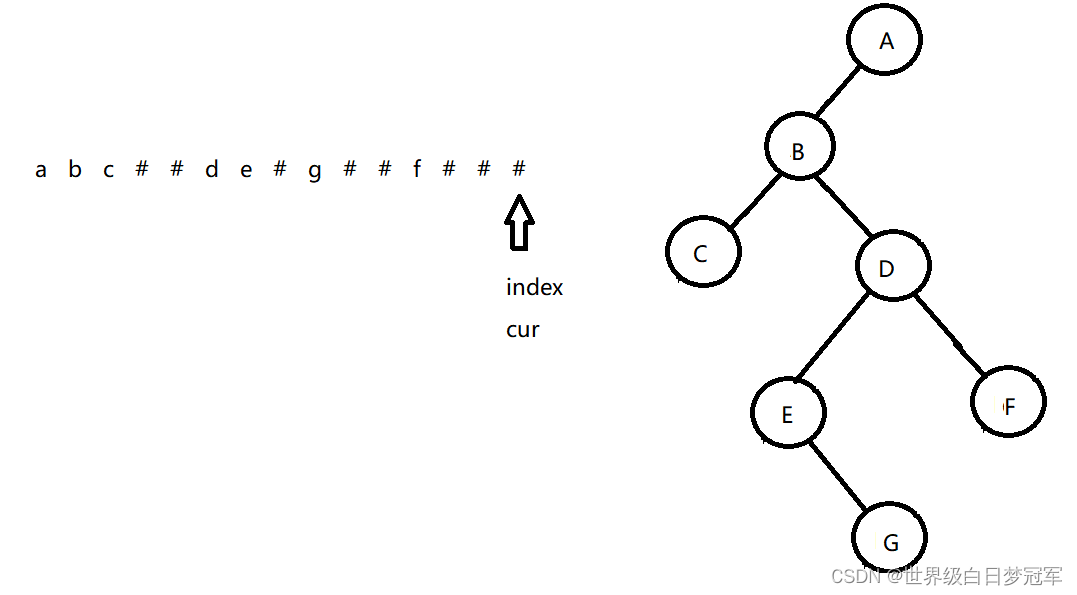
 到这儿位置就把完整的二叉树形成了。

class TreeNode{
    char val;
    TreeNode left;
    TreeNode right;
    public TreeNode(char val){
        this.val = val;
    }
}
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        while (in.hasNextLine()) {
            String s = in.nextLine();
            TreeNode root = preOrderBuild(s);
            inorder(root);
            index  = 0;
            System.out.println();
        }
    }
    public static void inorder(TreeNode root) {
        if(root==null){
            return ;
        }
        inorder(root.left);
        System.out.print(root.val+" ");
        inorder(root.right);
    }
    static int index = 0;
    public static TreeNode preOrderBuild(String s) {
        char cur = s.charAt(index);
        if(cur=='#'){
            index++;
            return null;
        }
        TreeNode root = new TreeNode(cur);
        index++;
        root.left = preOrderBuild(s);
        root.right = preOrderBuild(s);
        return root;
    }
}

二、从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

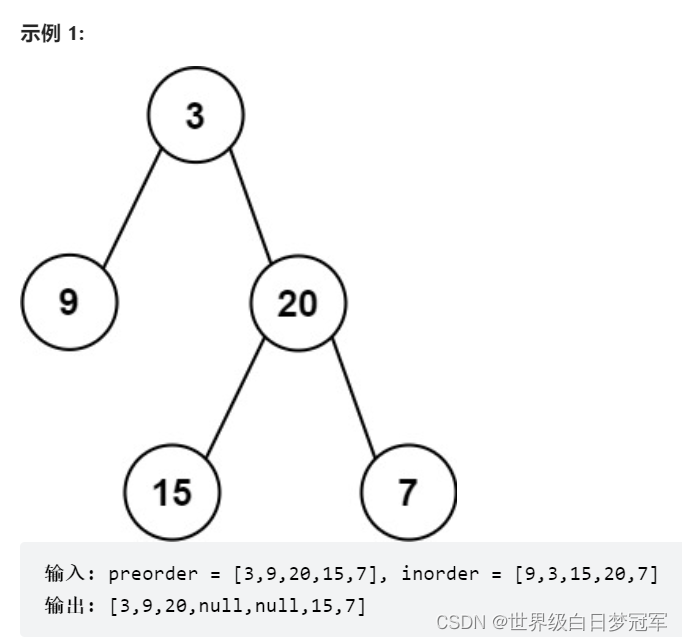
 前序遍历的第一个结果一定是当前树的根节点，中序遍历的左子树结果在树根的左侧，右子树结果在当前树根的右侧。

不断从前序遍历中取出树根节点，然后去中序遍历中查找当前树根所处的位置pos，他之前的是他的左子树，之后是右子树结点。

创建一个方法buildTreeHelper中借助前序遍历，在中序遍历的[left..right]还原二叉树，返回构造后的树根节点，有两个特殊情况，当left>right，此时区间为空，一个元素都没有直接返回null。当index == inorder.length，此时将整个前序遍历的所有元素全都访问完毕，构造结束，直接返回null。

在buildTree方法中直接返回buildTreeHelper中得到的值即可，传入两个数组、0和inorder的长度-1。

还需要创建一个find方法，即在当前中序遍历结果集中寻找val对应的位置下标，然后返回下标，就证明他之前的元素都是该位置元素的左子树，后面的都是右子树。

在buildTreeHelper方法中，创建一个全局变量index，进入方法，left为0，right为4，判断特殊情况之后，则证明树一定是有结点的，则创建一个TreeNode类型的root来存储preorder的0号下标位置的元素，然后index++，在创建一个变量pos，用来存储find方法找到的位置下标。

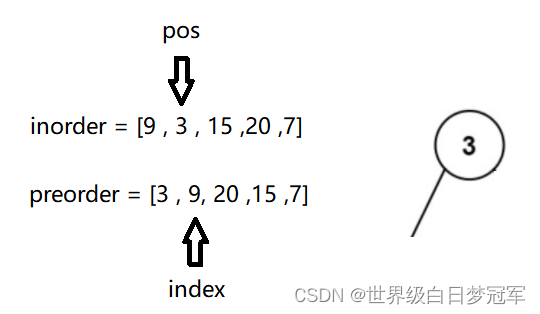
 然后调用root.left = buildTreeHelper(preorder,inorder,left,pos-1)，left为0，right为0，在创建root存储1号下标位置元素，然后index++，再用find方法寻找下标。

 然后调用root.left = buildTreeHelper(preorder,inorder,left,pos-1)，left为0，right为-1，发现left

然后调用root.right = buildTreeHelper(preorder,inorder,pos+1,right);left为1，right为0发现left(0)

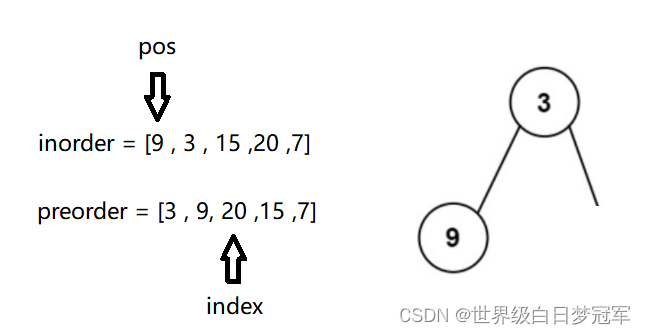
  然后root.right = buildTreeHelper(preorder,inorder,pos+1,right)，left为2，right为4，在创建root存储2号下标位置元素，然后index++，再用find方法寻找下标。

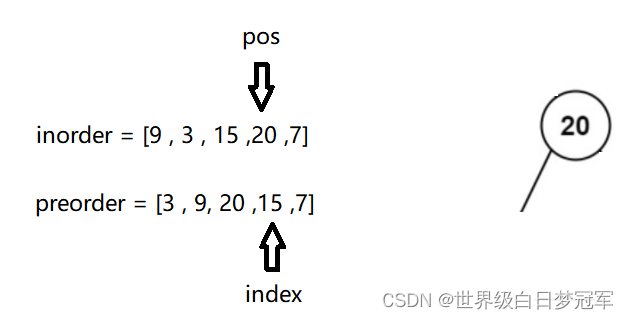
 然后调用root.left = buildTreeHelper(preorder,inorder,left,pos-1)，left为2，right为2，在创建root存储3号下标位置元素，然后index++，再用find方法寻找下标。

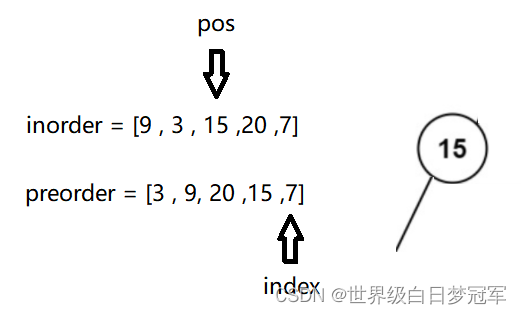
  然后调用root.left = buildTreeHelper(preorder,inorder,left,pos-1)，left为2，right为1，left>right，所以所以直接返回null，所以15的左子树也为null。

然后调用root.right = buildTreeHelper(preorder,inorder,pos+1,right);left为3，right为2，发现left(0)

 root.right = buildTreeHelper(preorder,inorder,pos+1,right);left为4，right为4，在创建root存储4号下标位置元素，然后index++，再用find方法寻找下标。

 然后调用root.left = buildTreeHelper(preorder,inorder,left,pos-1)，left为4，right为3，left>right，所以所以直接返回null，所以7的左子树为null。

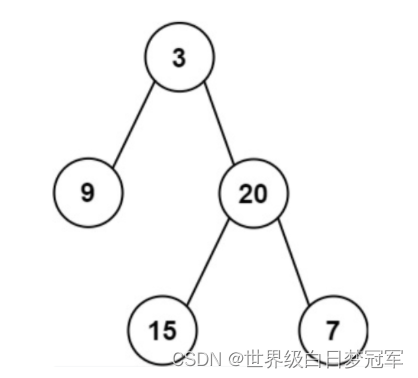
然后调用root.right = buildTreeHelper(preorder,inorder,pos+1,right);left为5，right为4，发现left>right，所以直接返回null，所以15的右子树也为null，那么直接返回root，所以20的右子树就建立成功了。

 所以将root返回，就得到了一棵完整的二叉树。

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return buildTreeHelper(preorder,inorder,0,inorder.length-1);
    }
    int index = 0;
    public TreeNode buildTreeHelper(int[] preorder, int[] inorder, int left, int right) {
        if(left>right){
            return null;
        }
        if(index==inorder.length){
            return null;
        }
        int rootVal = preorder[index];
        TreeNode root = new TreeNode(rootVal);
        index++;
        int pos = find(root.val,inorder);
        root.left = buildTreeHelper(preorder,inorder,left,pos-1);
        root.right = buildTreeHelper(preorder,inorder,pos+1,right);
        return root;
    }
    private int find(int val, int[] inorder) {
        for (int i = 0; i < inorder.length; i++) {
            if (inorder[i] == val) {
                return i;
            }
        }
        return -1;
    }

三、从中序遍历与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树。

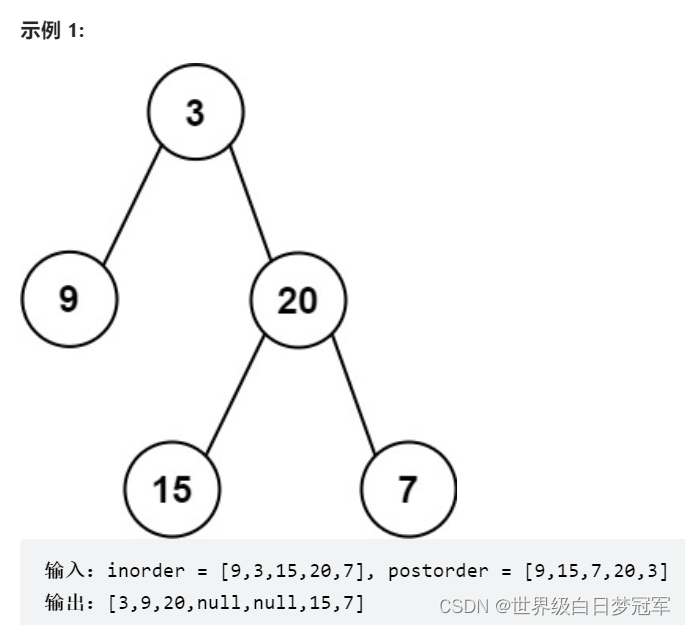
 我们知道后序遍历的导致就是根右左，所以我们创建一个reverse方法来翻转整个postorder数组，仍然也要创建一个find方法来查找当前元素的位置。

然后调用创建的buildTreeHelper方法，整个操作都是和之前一样的，不一样的在于先要调用root.right = buildTreeHelper(preorder,inorder,pos+1,right);后调用root.left = buildTreeHelper(preorder,inorder,left,pos-1);

public TreeNode buildTree(int[] inorder, int[] postorder) {
        postorder = reverse(postorder);
        return buildTreeHelper(postorder,inorder,0,inorder.length-1);
    }
    private int[] reverse(int[] postorder) {
        int[] arr = new int[postorder.length];
        int i = arr.length-1;
        for(int x :postorder){
            arr[i] = x;
            i--;
        }
        return arr;
    }
    int index = 0;
    public TreeNode buildTreeHelper(int[] preorder, int[] inorder, int left, int right) {
        if(left>right){
            return null;
        }
        if(index==inorder.length){
            return null;
        }
        int rootVal = preorder[index];
        TreeNode root = new TreeNode(rootVal);
        index++;
        int pos = find(root.val,inorder);
        root.right = buildTreeHelper(preorder,inorder,pos+1,right);
        root.left = buildTreeHelper(preorder,inorder,left,pos-1);
        return root;
    }
    private int find(int val, int[] inorder) {
        for (int i = 0; i < inorder.length; i++) {
            if (inorder[i] == val) {
                return i;
            }
        }
        return -1;
    }