PC_访存过程@内存地址翻译过程@具有快表TLB和cache的多级存储系统

PC_访存过程@内存地址翻译过程@具有快表TLB和cache的多级存储系统

具有TLB和Cache的多级存储系统

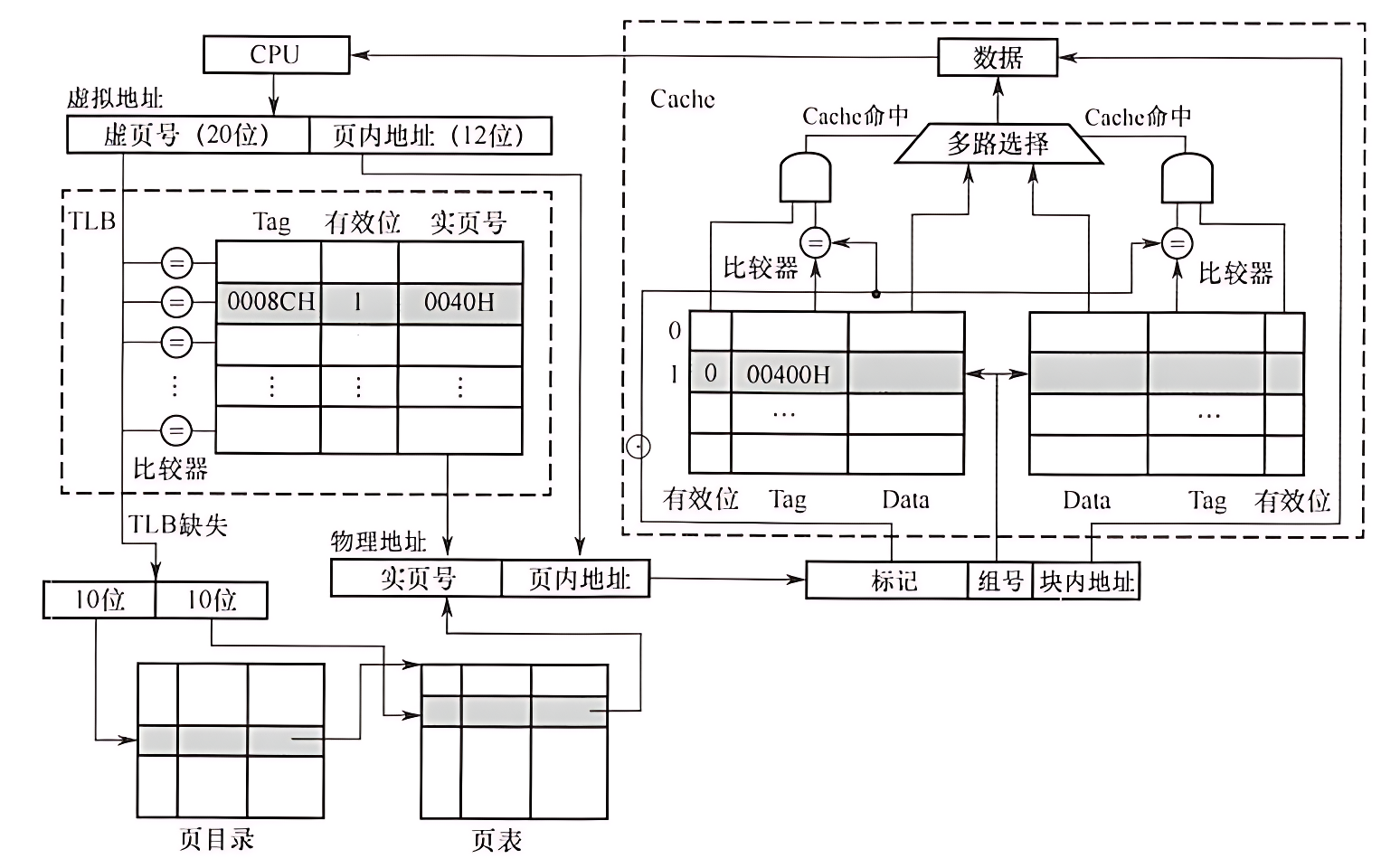
• 一个具有TLB和Cache的多级存储系统，其中Cache采用R=2路组相联方式
• CPU给出一个32位的虚拟地址，TLB采用全相联方式
  • 每一项都有一个比较器，查找时将虚页号与每个TLB标记字段同时进行比较，
  • 若有某一项相等且对应有效位为1，则TLB命中，此时可直接通过TLB进行地址转换：
  • 若未命中，则TLB缺失，需要访问主存去查页表。
  • 图中所示的是两级页表方式，虚页号被分成页目录索引和页表索引两部分，由这两部分得到对应的页表项，从而进行地址转换，并将相应表项调入TLB,若TLB已满，则还需要采用替换策略。
  • 完成由虚拟地址到物理地址的转换后，Cache机构根据映射方式将物理地址划分成多个字段
    • 然后根据映射规则找到对应的Cache行或组，将对应Cache行中的标记与物理地址中的高位部分进行比较，
  • 若相等且对应有效位为1，则Cache命中，此时根据块内地址取出对应的字送CPU。

• 查找时，快表和慢表也可以同步进行

  • 若快表中有此虚页号，则能很快地找到对应的实页号，并使慢表的查找作废，从而就能做到虽采用虚拟存储器但访问主存速度几乎没有下降。

三类缺失的可能情况组合

• 在一个具有Cache和TLB的虚拟存储系统中，CPU一次访存操作可能涉及5个地方的访问

  • 虚实地址转换(翻译)部分
    • TLB
    • 页表
    • 硬盘
  • 物理地址到cache映射部分
    • Cache
    • 主存
  • Note:结合访存过程,如果发生缺页,那么中断处理一定在虚实地址转换的环节完成(在cache映射之前)

• 根据乘法原理(方幂模型),理论上组合情况有$2^3=8种$

  • 但是只有部分情况会发生
  • 下面的表格将按照缺失程度(次数),从少到多排序(从最好的情况到最坏的情况)

• 情况	发生可能性说明	访存原因
  1	TLB命中则Page一定命中,信息在主存,就可能在 Cache 中
  2	TLB命中则 Page右定命中,信息在主存,也可能不在Cache中	cache缺失,需要访问内存,并且维护cache(可靠性和性能)
  3	TLB缺失但Page可能命中,信息在主存,就可能在Cache 中	快表TLB缺失,需要访问内存中的慢表查到目标(页面)物理地址,维护快表
  4	TLB缺失但Page可能命中,信息在主存,也可能不在 Cache中	有两个原因,分别是情况2,3的原因,同时维护TLB和cache
  5	TLB缺失则 Page也可能缺失,信息不在主存,也一定不在 Cache	由于内存发生缺页,需要进行1次硬盘IO;同时需要执行情况4需要做的工作

• 访问过程

  • CPU访存过程中存在三种缺失情况：
  • ①TLB缺失：要访问的页面的页表项不在TLB中：
  • ②Cache缺失：要访问的主存块不在Cache中：
  • ③Page缺失：要访问的页面不在主存中。(慢表缺失)
    • 第1种组合，无须访问主存
    • 第2种和第3种组合都需要访问一次主存：
    • 第4种组合需要访问两次主存：
    • 第5种组合发生“缺页异常”
      • 需要访问硬盘，
      • 并且至少访问两次主存

小结

• 主要看page是否命中
  • 如果是,根据TLB,Cache各自的命中情况(类比概率统计中抛两次硬币的情况)
    • 二元组:(TLB,cache),0表示缺失,1表示命中
      • (1,1)
      • (1,0)
      • (0,1)
      • (0,0)
  • 否则,TLB,cache就都不可能命中,仅有
    • 二元组:(TLB,cache),0表示缺失,1表示命中
      • (0,0)

cache缺失/内存缺页处理机构

• Cache缺失处理由硬件完成：
• 缺页处理由软件完成，操作系统通过“缺页异常处理程序”来实现
  • 而TLB缺失既可以用硬件又可以用软件来处理
  • TLB保存的是页表中活跃的部分项目

带TLB虚拟存储器的cpu访存过程

• PA:physical address
• VA:virtual address
• 大体过程:cpu给出虚拟地址VA,从VA计算出PA,由PA取得所需数据

  • 为了便于描述,🎈

    • 将VA单元所处的块(或者页)的物理地址为记:$b=PT[VA].b$
      • VA类似于页表对象PT的索引
      • b字段作为对象的成员

  • P0:VA$\to b$

  • P1:$b\to PA$

    • PA=b+W

  • P2:$PA\to (PA)$

    • 表示从计算出来的物理地址取出对应单元的数据

  • 上述两个过程的执行速度会有各种情况

    • 如果引入快表可以提升过程P1平均性能
    • 如果使用相联存储器,可以提升P2过程的平均性能

• cpu给出虚拟地址VA
  • 解析逻辑地址VA的字段:
    • 逻辑页号P
    • 页内偏移W
  • 检查快表TLB(转址旁路缓存器,是独立于内存的硬件)中的是否页(页表项)在TLB中
    • 如果有,则可以快速完成$P0:VA\to b$的转换过程(取得b)
    • 否则,意味着快表没未命中,需要访问位于内存中的慢表(branches)
      • 如果要访问的页面存在于内存中,那么需要2步操作(access page table & maintain TLB)
        • 访问内存中的慢表有望成功,可以取得b
        • 更新快表TLB(是为了下一次访存(执行P1过程能够有更高的几率走高速通道(快表,而不是慢表)))
          • 维护依据:局部性原理告诉我们这种亡羊补牢的操作是有效的
      • 否则就处于比较坏的情况了,需要访问硬盘(IO)
        • 空页框判断:检查内存中是否还有空闲页框可以分配
          • 如果有
            • 则可以直接从硬盘读取需要的块,调入主存中
            • 更新内存中的页表(包括慢表和快表TLB))
              • 同时为了下一次访问方便(减少IO次数/几率)
              • 维护根据:局部性原理
          • 否则,需要执行页面置换算法
            • 从主存中调出一页,然后在执行上一种情况(从硬盘调入缺失页面到内存)
  • 执行P1过程:计算$PA=b+W$
  • 判断物理地址PA是否在cache中存在(命中)
    • 如果命中,那么可以直接访问cache中的数据,完成访存(指存储器)任务
    • 否则cache缺失对应的页(块),需要将内容从主存(甚至需要先从硬盘调入内存)调入到cache.(branches):
      • 判断cache中是否空闲行可以容纳新的块
        • 如果是,那么直接从内存中调入调入缺失的块到cache中
        • 否则,需要执行cache块的置换算法,从cache中调出一块内容(可能写回内存)
          • 然后在把缺失的页面调入到刚才空出的cache行中
      • 调整完cache行内容后还需要修改新内容的cache行对应的标记位和有效位
  • 过程P2:从cache中将需要的内容读取使用,结束该次访存

例

• 当TLB缺失(未命中)时,需要到内存中的慢表进行查询
  • 设某存储系统包含一个TLB和一个data Cache(数据cache)
  • 存储器以字节为编址单位
  • 虚拟地址(逻辑地址)为$n_v=$14bit
  • 物理地址为$n_p=12$bit
  • 页面大小为64B
    • 可知页内偏移为b=$\log_2{64}=$6bit
  • TLB快表采用$R_v$=4路组相联,并设有$C_v=16$个条目
  • dataCache采用物理寻址
    • cache行大小为4B
      • 则行内偏移为2bit
    • 共有16组
      • cache组索引有${\log }_{2}16=4$bit

分析

虚拟地址:

• 低6位为页内地址

• 高14-6=8位是虚拟页号

• 慢表的结构和快表有所不同

• 则有Q=$\frac{C_v}{R_v}=16/4=4$个组

  • 虚拟页号中的低2=${\log }_{2}4$位作为组索引
  • 其余$8-2=6$bit作为TLB标记位字段

• 综上,虚拟地址结构:

  • 虚拟页号8bit
    • TLB标记位6bit
    • 组索引号2bit
  • 页内索引6bit

物理地址

• 物理地址位数位12位
  • 物理页号位数12-6=6bit
  • cache对物理地址的划分(高m位+低b位)
    • cache行大小为4B,所以可以确定cache行内偏移位数b=${\log }_{2}4=2$bit
      • 视上下文含义在cache行中又可以分为若干字块
    • m=12-2=10bit
      • 又由于行cache组索引为4bit
      • 所以剩余s=10-4=6bit作为cache标记
  • 综上,物理地址换分为(从高到低)
    • 6位cache标记位(同时也是物理页号位数)
    • 6位页内偏移
      • 4位cache组索引
      • 2位cache行内偏移

Note:字段位数和补齐

• 每个字段的位数都是固定的
• 及时进制转换过程中高位是0(或者位数不足)也应该补0对齐!!

TLB命中/缺失

• 慢表的结构和快表有所不同

  • 查询TLB时,用虚地址组索引字段的2位去查找
    • 如果标记位和虚地址的标记位字段一致,并且有效位为1,则命中
    • 可以TLB表项的物理页号字段和虚拟地址的页内偏移字段合成物理地址(字地址)
  • 当TLB缺失时,需要用虚拟页号去访问慢表
    • 如果存在相应的虚拟页号,那么访问的地址单元所在页面存在于内存中
    • 否则产生缺页中断